Chưa có sản phẩm trong giỏ hàng.
Tổng hợp các dạng toán nâng cao lớp 3 có đáp án
Bài viết “Tổng hợp các dạng toán nâng cao lớp 3 có đáp án” dưới đây của Tkbooks sẽ cung cấp các dạng bài toán nâng cao lớp 3 thường gặp nhất trong các kỳ thi học sinh giỏi kèm theo đáp án chi tiết để các em học sinh có thể tự học và ôn luyện một cách dễ dàng.
Mời quý phụ huynh và các bạn học sinh tham khảo!
>>> Xem thêm:
Bài tập phép cộng trừ không nhớ trong phạm vi 1000 PDF
Bài tập phép cộng trừ có nhớ trong phạm vi 1000 PDF
Bài tập phép nhân lớp 3 – Nhân số có 2, 3, 4, 5 chữ số kèm file PDF
I. Dạng toán Tính nhanh
Dạng toán nâng cao lớp 3 về Tính nhanh là các bài toán yêu cầu học sinh phải sử dụng các kỹ năng và mẹo tính toán để thực hiện phép tính một cách nhanh chóng và chính xác.
Dưới đây là một số ví dụ về dạng toán tính nhanh thường gặp:
Ví dụ 1: Tính nhanh
a) A = (a x 7 + a x 8 – a x 15) : ( 1 + 2 + 3 + …….. + 10)
b) B = (18 – 9 x 2) x ( 2 + 4 + 6 + 8 + 10)
Lời giải:
a) A = (a x 7 + a x 8 – a x 15) : ( 1 + 2 + 3 + …….. + 10)
A = a x (7 + 8 – 15) : (1 + 2 + 3 + …….. + 10)
A = (a x 0) : (1 + 2 + 3 + …….. + 10)
A = 0 : (1 + 2 + 3 + …….. + 10)
A = 0
b) B = (18 – 9 x 2) x (2 + 4 + 6 + 8 + 10)
B = (18 – 18) x ( 2 + 4 + 6 + 8 + 10)
B = 0 x (2 + 4 + 6 + 8 + 10)
B = 0
Ví dụ 2: Tính nhanh
a) 24 x 5 + 24 x 3 + 24 x 2
b) 217 x 45 + 50 x 217 + 217 x 5
Lời giải:
a) 24 x 5 + 24 x 3 + 24 x 2
= 24 x (5 + 3 + 2)
= 24 x 10
= 240
b) 217 x 45 + 50 x 217 + 217 x 5
= 217 x (45 + 50 + 5)
= 217 x 100
= 21700
Ví dụ 3: Tính nhanh tổng sau: 3 + 7 + 11 + …….+ 75.
Lời giải:
Ta viết tổng 3 + 7 + 11 + …….+ 75 với đầy đủ các số hạng như sau:
= 3 + 7 + 11 + 15 + 19 + 23 + 27 + 31 + 35 + 39 + 43 + 47 + 51 + 55 + 59 + 63 + 67 + 71 + 75.
= (3 + 75) + (7 + 71) + (11 + 67) + (15 + 63) + (19 + 59) + (23 + 55) + (27 + 51) + (31 + 47) + (35 + 43) + 39
= 78 + 78 + 78 + 78 + 78 + 78 + 78 + 78 + 78 + 39
= 78 x 9 + 39
= 702 + 39
= 741
II. Dạng toán Tính giá trị của biểu thức
Dạng toán nâng cao lớp 3 về Tính giá trị của biểu thức yêu cầu học sinh phải tính toán giá trị của các biểu thức toán học bằng cách thực hiện các phép tính theo đúng thứ tự ưu tiên. Dưới đây là một số ví dụ và phương pháp giải cho dạng toán này:
Ví dụ 1: Tính giá trị biểu thức:
a) 63 : 7 + 24 x 2 – ( 81 – 72)
b) 27 x 2 + 5 x 27 + 27 x 3
Lời giải:
a) 63 : 7 + 24 x 2 – ( 81 – 72)
= 63 : 7 + 24 x 2 – 9
= 9 + 24 x 2 – 9
= 9 + 48 – 9
= 48
b) 27 x 2 + 5 x 27 + 27 x 3
= 27 x (2 + 5 + 3)
= 27 x 10
= 270
Ví dụ 2: Tính giá trị của biểu thức sau:
Tính biểu thức sau bằng cách thuận tiện nhất :
a) (6 x 8 – 48) : (10 + 11 + 12 + 13 + 14 + 15)
b) 32764 – 2467 + 236 + 3467
Lời giải:
a) (6 x 8 – 48) : (10 + 11 + 12 + 13 + 14 + 15)
= (48 – 48) : (10 + 11 + 12 + 13 + 14 + 15)
= 0 : (10 + 11 + 12 + 13 + 14 + 15)
= 0
b) 32764 – 2467 + 236 + 3467
= (32764 + 236 ) + (3467 – 2467)
= 33000 + 1000
= 34000
Ví dụ 3: Viết biểu thức sau thành tích 2 thừa số rồi tính giá trị của biểu thức đó:
a) 15 x 5 + 3 x 5 + 5 x 2 – 10 x 5
b) (24 + 6 x 5 + 6) – (12 + 6 x 3)
c) 23 + 39 + 37 + 21 + 34 + 26
Lời giải:
a) 15 x 5 + 3 x 5 + 5 x 2 – 10 x 5
= 5 x (15 + 3 + 2 – 10)
= 5 x 10
= 50
b) (24 + 6 x 5 + 6 ) – (12 + 6 x 3)
= (6 x 4 + 6 x 5 + 6 x 1) – (6 x 2 + 6 x 3)
= 6 x (4 + 5 + 1) – 6 x (2 + 3)
= 6 x 10 – 6 x 5
= 6 x (10 – 5)
= 6 x 5
= 30
c) 23 + 39 + 37 + 21 + 34 + 26
= (23 + 37) + (39 + 21) + (34 + 26)
= 60 + 60 + 60
= 60 x 3
= 180
III. Dạng toán lớp 3 nâng cao Tìm x
Dạng toán nâng cao lớp 3 về Tìm x là các bài toán yêu cầu học sinh tìm giá trị của ẩn số x trong các phương trình hoặc biểu thức. Dưới đây là một số ví dụ và phương pháp giải cho dạng toán này:
Ví dụ 1: Tìm X
a) X x 5 + 122 + 236 = 633
b) (X : 12) x 7 + 8 = 36
Lời giải:
a) X x 5 + 122 + 236 = 633
X x 5 + 358 = 633
X x 5 = 633 – 358
X x 5 = 275
X = 275 : 5
X = 55
b) (X : 12) x 7 + 8 = 36
(X : 12) x 7 = 36 – 8
(X : 12) x 7 = 28
X : 12 = 28 : 7
X : 12 = 4
X = 4 x 12
X = 48
Ví dụ 2: Tìm x:
a) 72 – x : 4 = 16
b) 72 : x – 3 = 5
Lời giải:
a) 72 – x : 4 = 16
x : 4 = 72 – 16
x : 4 = 56
x = 56 x 4
x = 224
b) 72 : x – 3 = 5
72 : x = 5 + 3
72 : x = 8
x = 72 : 8
x = 9
Ví dụ 3: Tìm x
a) x – 452 = 77 + 48
b) x + 58 = 64 + 58
Lời giải:
a) x – 452 = 77 + 48
x – 452 = 125
x = 125 + 452
x = 577
b) x + 58 = 64 + 58
x + 58 = 122
x = 122 – 58
x = 64
IV. Dạng toán lớp 3 nâng cao về Dãy số
Dạng toán nâng cao lớp 3 về dãy số, số chẵn, số lẻ là các bài toán yêu cầu học sinh hiểu và vận dụng các quy tắc về dãy số cũng như thực hiện các phép tính liên quan đến chúng. Dưới đây là một số ví dụ và phương pháp giải cho dạng toán này:
Ví dụ 1: Dãy số tự nhiên liên tiếp bắt đầu từ 48 đến 126 có bao nhiêu số chẵn, bao nhiêu số lẻ? Có bao nhiêu chữ số?
Lời giải:
Dãy số tự nhiên liên tiếp từ 48 đến 126 có: (126 – 48) : 1 + 1 = 79 (số)
Dãy số bắt đầu là số chẵn kết thúc là số chẵn thì số lượng số chẵn hơn số lượng số lẻ 1 số.
2 lần số lẻ là: 79 – 1 = 78 (số)
Số lẻ là: 78 : 2 = 39 (số)
Số chẵn là: 39 + 1 = 40 (số)
Đáp số: Số lẻ: 39 số; Số chẵn: 40 số
Từ 48 đến 99 có: (99 – 48) : 1 + 1 = 52 (số)
Từ 100 đến 126 có: (126 – 100) : 1 + 1 = 27 (số)
Số các chữ số là: 52 x 2 + 27 x 3 = 185 (chữ số)
Đáp số: 185 chữ số
Ví dụ 2: Bạn An viết dãy số : 1, 0, 0, 1, 0, 0, 1, 0, 0, 1…(Bắt đầu là số 1, tiếp đến 2 số 0 rồi lại đến số 1, …). Hỏi:
a) Số hạng thứ 31 là số 1 hay số 0?
b) Khi viết đến số hạng thứ 100 thì ta viết bao nhiêu số 1, bao nhiêu số không?
Lời giải:
Gọi (1, 0, 0) làm một nhóm
a) Ta có: 31 : 3 = 10 (dư 1)
Vậy số hạng thứ 31 sẽ là số đầu tiên của nhóm tiếp theo. Vậy số hạng thứ 31 là số 1.
b) Ta có 100 : 3 = 33 (dư 1)
Như vậy khi viết đến số hạng thứ 100 ta viết được 33 nhóm và thêm 1 số 1
Vậy số các số 1 là: 33 x 1 + 1 = 34 (số)
Số các số 0 là: 33 x 2 = 66 (số)
Đáp số: 34 số 1; 66 số 0
Ví dụ 3: Cho dãy số : 2, 4, 6, 8, 10, 12, … Hỏi:
a) Số hạng thứ 20 là số nào?
b) Số 93 có ở trong dãy trên không? Vì sao?
Lời giải
a) Dãy số trên là dãy số cách đều 2 đơn vị.
Số hạng thứ 20 trong dãy trên là:
2 + (20 – 1) x 2 = 40
Đáp số: 40
b) Số 93 có ở trong dãy trên không? Vì sao?
Số 93 không có trong dãy trên vì dãy số trên là dãy số chẵn cách đều 2 đơn vị mà số 93 là số lẻ nên số 93 không có trong dãy số trên.
V. Dạng toán về tích các số
Dạng toán nâng cao lớp 3 về tích các số bao gồm các bài toán yêu cầu học sinh thực hiện các phép tính nhân để tìm ra tích của các số hoặc giải quyết các bài toán ứng dụng liên quan đến phép nhân. Dưới đây là một số ví dụ và phương pháp giải cho dạng toán này:
Ví dụ 1: Tích của hai số là 354. Nếu thừa số thứ nhất tăng lên 3 lần thừa số thứ hai tăng lên 2 lần thì tích mới là bao nhiêu?
Lời giải:
Nếu thừa số thứ nhất tăng lên 3 lần thừa số thứ hai tăng lên 2 lần thì tích tăng là: 3 x 2 = 6 (lần)
Tích mới là: 354 x 6 =2124
Đáp số: 2124
Ví dụ 2: Tích của 2 số là 645. Tìm thừa số thứ nhất, biết rằng nếu thêm 5 đơn vị vào thừa số thứ hai thì tích mới sẽ là 860.
Lời giải:
Nếu thêm 5 đơn vị vào thừa số thứ hai thì tích tăng 5 lần thừa số thứ nhất.
5 lần thừa số thứ nhất là: 860 – 645 = 215 (đơn vị)
Thừa số thứ nhất là: 215 : 5 = 43
Đáp số: 43
Ví dụ 3: Tích của hai số là 75. Bạn An viết thêm chữ số 0 vào bên phải thừa số thứ nhất và giữ nguyên thừa số thứ hai rồi nhân hai số với nhau. Hỏi tích mới là bao nhiêu?
Lời giải:
Bạn An viết thêm chữ số 0 vào bên phải thừa số thứ nhất tức là thừa số thứ nhất được tăng lên 10 lần.
Nếu tăng thừa số thứ nhất lên 10 lần và giữ nguyên thừa số thứ hai thì tích tăng lên 10 lần.
Tích mới là: 75 x 10 = 750
Đáp số: 750
VI. Dạng toán Tính thời gian
Dạng toán nâng cao lớp 3 về tính thời gian bao gồm các bài toán yêu cầu học sinh tính toán và hiểu rõ về các khái niệm liên quan đến thời gian, như tính toán khoảng thời gian, xác định thời gian kết thúc hoặc bắt đầu một sự kiện, và thực hiện các phép tính cộng trừ thời gian. Dưới đây là một số ví dụ và phương pháp giải cho dạng toán này:
Ví dụ 1:
Hồng hỏi Cúc: “Bây giờ là mầy giờ chiều ?”.Cúc trả lời: “Thời gian từ lúc 12 giờ trưa đến bây giờ bằng 1/3 thời gian từ bây giờ đến nửa đêm (tức 12 giờ đêm hôm nay)”.
Em hãy tính xem bây giờ là mấy giờ.
Lời giải:
Từ 12 giờ trưa đến 12 giờ đêm có 12 giờ
Ta có sơ đồ:
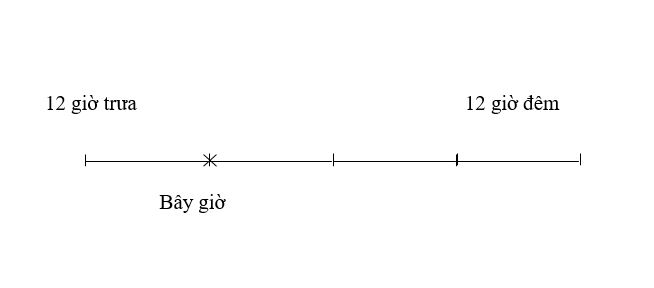
Từ 12 giờ trưa đến bây giờ đã qua số thời gian là: 10 : (1 + 3) = 4 (giờ)
Vậy bây giờ là 15 giờ (12 + 3 = 15) hay 3 giờ chiều.
Đáp số: 3 giờ chiều
Ví dụ 2: Thứ năm tuần này là ngày 25 tháng 3. Hỏi thứ năm tuần sau là ngày nào?
Lời giải:
Tháng 3 có 31 ngày.
Vì thứ năm tuần này cách thứ năm tuần sau 7 ngày nên thứ năm tuần sau là ngày 1 tháng 4.
Đáp số: Ngày 1 tháng 4.
Ví dụ 3: Cùng một quãng đường, ô tô thứ nhất chạy hết 1/4 giờ, ô tô thứ hai chạy hết 16 phút, ô tô thứ ba chạy hết 1/5 giờ. Hỏi ô tô nào chạy nhanh nhất?
Lời giải:
Đổi: 1 giờ = 60 phút
Ô tô thứ nhất chạy hết số thời gian là: 60 : 4 = 15 (phút)
Ô tô thứ ba chạy hết số thời gian là: 60 : 5 = 14 (phút)
Vậy ô tô thứ ba chạy nhanh nhất.
VII. Dạng toán về Chu vi hình chữ nhật
Dạng toán nâng cao lớp 3 về chu vi hình chữ nhật yêu cầu học sinh hiểu và áp dụng công thức tính chu vi của hình chữ nhật, cũng như giải quyết các bài toán ứng dụng liên quan. Chu vi của hình chữ nhật được tính bằng tổng độ dài các cạnh của nó. Dưới đây là một số ví dụ và phương pháp giải cho dạng toán này:
Ví dụ 1: Một hình chữ nhật có chu vi 72cm. Nếu giảm chiều rộng đi 6cm và giữ nguyên chiều dài thì diện tích giảm đi 120cm2. Tính chiều dài và chiều rộng hình chữ nhật đó.
Lời giải:
Chiều dài hình chữ nhật là: 120 : 6 = 20 (cm)
Nửa chu vi hình chữ nhật là: 72 : 2 = 36 (cm)
Chiều rộng hình chữ nhật là: 36 – 20 = 16 (cm)
Đáp số: Chiều dài: 20cm; Chiều rộng: 16cm.
Ví dụ 2: Người ta trồng chuối xung quanh một mảnh đất hình chữ nhật có chiều rộng là 8m, chiều rộng bằng 1/5 chiều dài. Hỏi xung quanh mảnh đất đó trồng được bao nhiêu cây chuối, biết rằng hai cây chuối trồng cách nhau 4m?
Lời giải:
Chiều dài của mảnh đất là: 8 x 5 = 40 (m)
Chu vi mảnh đất là: (8 + 40) x 2 = 96 (m)
Xung quanh mảnh đất đó trồng được số cây chuối là: 96 : 4 = 24 (cây)
Đáp số: 24 cây
Ví dụ 3: Một hình chữ nhật có chu vi là 80cm. Nếu tăng chiều dài 5cm thì diện tích tăng 75cm2. Tính chiều dài, chiều rộng hình chữ nhật đó.
Lời giải:
Theo đề bài ta có hình vẽ sau:
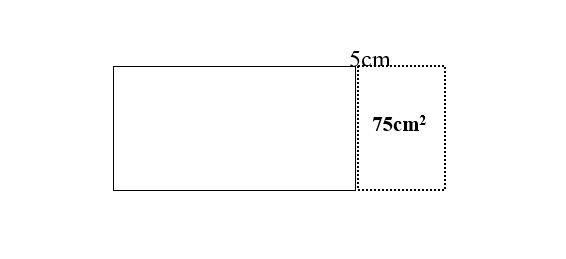
Chiều rộng của hình chữ nhật là: 75 : 5 = 15 (cm)
Nửa chu vi là: 80 : 2 = 40 (cm)
Chiều dài của hình chữ nhật là: 40 – 15 = 25 (cm)
Đáp số: chiều dài: 25cm; chiều rộng: 15cm.
VIII. Dạng toán có lời văn
Dạng toán nâng cao lớp 3 có lời văn là những bài toán yêu cầu học sinh đọc và hiểu nội dung của một đoạn văn, sau đó sử dụng các kỹ năng toán học để giải quyết các vấn đề được đưa ra. Dưới đây là một số ví dụ và phương pháp giải cho dạng toán này:
Ví dụ 1: Từ ba chữ số 6, 7 , 9 ta lập được một số có ba chữ số khác nhau là A. Từ hai số 5, 8 ta lập được một số có hai chữ số khác nhau là B. Biết rằng hiệu giữa A và B là 891. Tìm hai số đó?
Lời giải:
Biết hiệu giữa A và B là 891 tức là số có 3 chữ số phải lớn hơn 891.
Từ ba chữ số 6, 7, 9 ta lập được số có ba chữ số khác nhau lớn hơn 891 là: 976, 967.
Từ hai số 5, 8 ta lập được số có hai chữ số khác nhau là: 58 và 85.
Ta có các trường hợp sau:
976 – 58 = 918 (loại)
976 – 85 = 891 (chọn)
967 – 58 = 909 (loại)
967 – 85 = 882 (loại)
Vậy hai số đó là: 976 và 85.
Ví dụ 2: Trong túi có ba loại bi: bi đỏ, bi vàng và bi xanh. Biết rằng số bi của cả túi nhiều hơn tổng số bi vàng và bi đỏ là 15 viên, số bi xanh ít hơn số bi vàng là 3 viên và nhiều hơn bi đỏ là 4 viên. Hỏi trong túi có bao nhiêu viên bi?
Lời giải:
Số bi của cả túi nhiều hơn tổng số bi vàng và bi đỏ là 15 viên tức là số bi xanh là 15 viên
Số bi vàng là: 15 + 3 = 18 (viên)
Số bi đỏ là: 15 – 4 = 11 (viên)
Trong túi có tất cả số bi là: 15 + 18 + 11 = 44 (viên)
Đáp số: 44 viên
Ví dụ 3: Một cửa hàng có 1245 cái áo. Ngày thứ nhất cửa hàng bán 1/3 số áo. Ngày thứ hai cửa hàng bán 1/5 số áo còn lại. Hỏi sau hai ngày bán cửa hàng còn lại bao nhiêu cái áo?
Lời giải:
Ngày thứ nhất bán được số cái áo là: 1245 : 3 = 415 (cái áo)
Số áo còn lại của cửa hàng sau ngày thứ nhất là: 1245 – 415 = 830 (cái áo)
Ngày thứ hai cửa hàng bán được số áo là: 830 : 5 = 166 (cái áo)
Cửa hàng còn lại số áo là: 830 – 166 = 664 (cái áo)
Đáp số: 664 cái áo
IX. Dạng toán Tìm số
Dạng toán nâng cao lớp 3 về Tìm số bao gồm các bài toán yêu cầu học sinh tìm ra số thỏa mãn các điều kiện hoặc quy tắc nhất định. Dưới đây là một số ví dụ và phương pháp giải cho dạng toán này:
Ví dụ 1: Tích của 2 số là 645. Tìm thừa số thứ nhất, biết rằng nếu thêm 5 đơn vị vào thừa số thứ hai thì tích mới sẽ là 860.
Lời giải:
Nếu thêm 5 đơn vị vào thừa số thứ hai thì tích tăng 5 lần thừa số thứ nhất.
5 lần thừa số thứ nhất là: 860 – 645 = 215 (đơn vị)
Thừa số thứ nhất là: 215 : 5 = 43
Đáp số: 43
Ví dụ 2: An nghĩ một số. Nếu gấp số đó lên 3 lần rồi cộng với 15 thì được 90. Tìm số An đã nghĩ.
Lời giải:
Gọi số An nghĩ ra là x. Theo đề bài ta có:
X x 3 + 15 = 90
(X x 3) + 15 = 90
X x 3 = 90 – 15
X x 3 = 75
X = 75 : 3
X = 25
Vậy số An nghĩ ra là 25.
Ví dụ 3: Tìm số có 3 chữ số, biết rằng khi xoá bỏ chữ số 7 ở hàng đơn vị, ta được số mới kém số phải tìm là 331.
Lời giải:
Khi xoá bỏ chữ số 7 ở hàng đơn vị của số có 3 chữ số thì số đó giảm đi 7 đơn vị rồi giảm đi 10 lần.
Ta có sơ đồ sau:
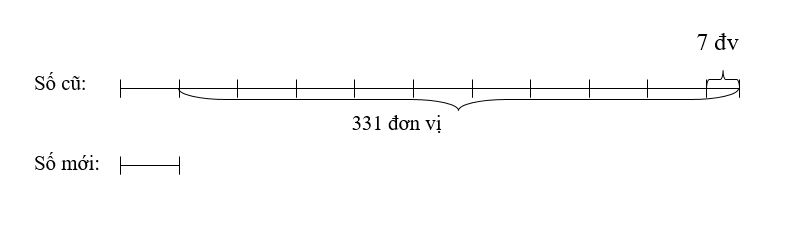
Nếu số cũ bớt đi 7 đơn vị thì số cũ hơn số mới là: 331 – 7 = 324 (đơn vị)
324 đơn vị ứng với số phần là: 10 – 1 = 9 (phần)
Số mới là: 324 : 9 = 36
Số cũ là: 36 x 10 + 7 = 367
Đáp số: 367.
Hy vọng rằng bài viết “Tổng hợp các dạng toán nâng cao lớp 3 có đáp án” trên đã mang đến cho các em học sinh và phụ huynh những dạng bài tập Toán nâng cao lớp 3 điển hình cũng như phương pháp giải chi tiết để các em có thể tự tin chinh phục các kỳ thi học sinh giỏi.
Những bài toán cơ bản và nâng cao lớp 3 đều có sẵn trong cuốn Bài tập bổ trợ nâng cao Toán lớp 3 và 50 đề tăng điểm nhanh Toán lớp 3 của Tkbooks. Phụ huynh có thể tham khảo và mua cho con để con có thể khám phá thêm nhiều bài Toán thú vị khác.
Link đọc thử sách Bài tập bổ trợ nâng cao Toán lớp 3: https://drive.google.com/file/d/1k3TqDSkOm9W0eBI97Np_tBRyiYhSMHy2/view
Link đọc thử sách 50 đề tăng điểm nhanh Toán lớp 3: https://drive.google.com/file/d/1vATwExyU4MMnNiCN4l5o7IuVQlIn7ctZ/view
Đặt sách để nhận khuyến mãi lên đến 20%:

Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 3 hàng đầu tại Việt Nam!


