Chưa có sản phẩm trong giỏ hàng.
Số phức là gì? Lý thuyết, bài tập và cách giải cực chi tiết
Số phức là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.
Dưới đây là toàn bộ kiến thức về Số phức bao gồm số phức là gì, phép cộng trừ nhân chia số phức và bài tập về số phức. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
I. SỐ PHỨC LÀ GÌ?
1. Khái niệm số phức
Mỗi biểu thức dạng a + bi, trong đó a, b ∈ R, i2 = -1 được gọi là một số phức.
Đối với số phức z = a + bi, ta nói a là phần thực, b là phần ảo của z.
Tập hợp các số phức ký hiệu là C.
Lưu ý:
- z là số thực khi b = 0
- z là số ảo (thuần ảo) khi a = 0.
- Số 0 vừa là số thực vừa là số ảo.

2. Hai số phức bằng nhau
Cho hai số phức z1 = a + bi (a;b ∈ R ) và z1 = c + di (c;d ∈ R).
Ta có z1 = z2 ⇔ a = c và b = d.
3. Biểu diễn hình học số phức
Số phức z = a + bi (a;b ∈ R) được biểu diễn bởi điểm M(a;b) hay bởi → u = (a;b) trong mặt phẳng tọa độ.

4. Phép cộng và phép trừ số phức
Cho hai số phức z1 = a + bi (a;b ∈ R ) và z2 = c + di (c;d ∈ R). Khi đó:
z₁ + z₂ = (a + c) + (b + d).i.
z₁ – z₂ = (a – c) + (b – d).i.
Số đối của số phức z = a + b.i là: -z = -a – b.i.
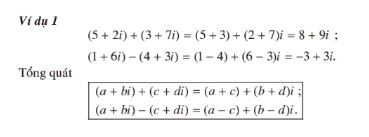
5. Phép nhân số phức
z₁.z₂ = (a + b.i)(c + d.i) = (ac − bd) + (ad +bc).i .
k.z = k.(a + b.i) = k.a + k.b.i (k∈R).
Đặc biệt: 0.z = 0 với ∀z.
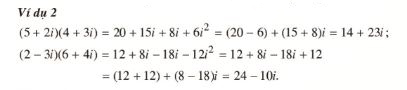
6. Số phức liên hợp

7. Môđun của số phức
Môđun của số phức z = a + bi ( a;b ∈ R ) là số thực không âm √(a2 + b2) và được ký hiệu là:
| |z| = √(a2 + b2) |
Một số tính chất:
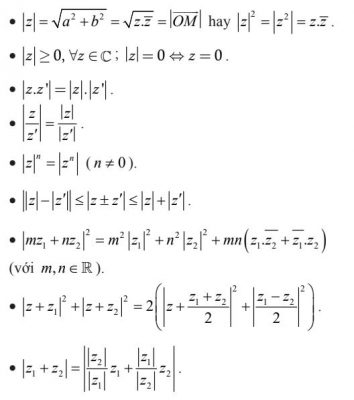
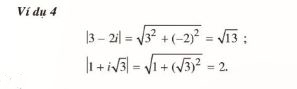
8. Chia hai số phức


9. Lũy thừa đơn vị ảo i
iº = 1, i1 = i, i² = -1, i3 = i².i = -i, … ,
i4n = 1, i4n+1 = i, i4n+2 = -1, i4n+3 = -i, ∀n∈N*.
Do đó: in ∈ {−1;1;-I;i},∀n∈N*.
II. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
1. Căn bậc hai của số thực âm
Tương tự căn bậc hai của một số thực dương, từ đẳng thức i2 = −1, ta nói i là một căn bậc hai của −1 ; − i cũng là một căn bậc hai của −1, vì (−i)2 = -1.
Từ đó, ta xác định được căn bậc hai của các số thực âm, chẳng hạn:
- Căn bậc hai của –2 là ±i√2, vì (±i√2)2 = -2
- Căn bậc hai của –3 là ±i√3, vì (±i√3)2 = -3
- Căn bậc hai của –4 là ±i√4, vì (±i√4)2 = -4.
Tổng quát, các căn bậc hai của số thực a âm là: ±i√|a|
2. Phương trình bậc hai với hệ số thực
Cho phương trình bậc hai ax’+ bx + c = 0 với a,b,c ∈ R và a ≠ 0.
Xét biệt thức Δ = b2 – 4ac của phương trình. Ta thấy:

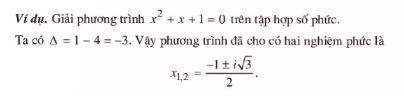
III. QUỸ TÍCH SỐ PHỨC

Tìm tất cả các số phức z có môdun nhỏ nhất thỏa mãn điều kiện cho trước:
- Bước 1: Tìm tập hợp điểm M(x;y) biểu diễn số phức z = x + yi để được mối liên hệ x, y.
- Bước 2: Dựa vào mối liên hệ giữa x và y ở bước 1 để tìm |z|min và |z|max.
IV. DẠNG LƯỢNG GIÁC CỦA SỐ PHỨC
1. Khái niệm về dạng lượng giác của số phức
Số phức z = r(cosφ + isinφ) được gọi là dạng lượng giác của số phức.
Trong đó:
- r: là module của số phức.
- φ : là argument của số phức.
2. Cách chuyển đổi một số phức từ dạng đại số sang dạng lượng giác
Để chuyển số phức z = a + bi sang dạng lượng giác z = r(cosφ + isinφ) ta phải tìm được module và argument của số phức.
Bằng việc đồng nhất biểu thức hai số phức, ta có:
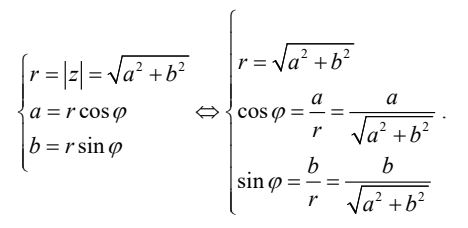
3. Nhân và chia số phức dưới dạng lượng giác
Cho hai số phức z = r(cosφ + isinφ) và z’ = r'(cosφ’ + isinφ’) với r; r’ > 0.
Ta có z.z’ = r.r'[cos(φ + φ’) + isin(φ + φ’)];
z/z’ = r/r’[cos(φ – φ’) + isin(φ – φ’)];
4. Công thức Moivre
Với n∈N* thì:
[r(cosφ + isinφ)]n = rn(cos nφ + isin nφ)
5. Căn bậc hai của số phức dưới dạng lượng giác
Căn bậc hai của số phức z = r(cosφ + isinφ) với r > 0 là:
√r.(cosφ/2 + isin φ/2) và
-√r.(cosφ/2 + isin φ/2) = √r.[(cos(φ/2 + π) + isin (φ/2 + π)].
V. Bài tập
Dưới đây là một số dạng toán cơ bản về Số phức để các em luyện tập:

Các dạng toán khác về Số phức được ghi chú và diễn giải rất đầy đủ trong cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.


