Các bài toán lớp 5 – Hướng dẫn giải chi tiết từng dạng toán

Các bài toán lớp 5 kèm hướng dẫn giải chi tiết từng dạng toán trong bài viết dưới đây sẽ giúp các em học sinh nắm chắc kiến thức, rèn kỹ năng giải toán và tự tin hơn trong học tập cũng như các kỳ kiểm tra.

Mời các em tham khảo!

1. Bài toán cấu tạo số lớp 5

a) Cấu tạo hàng của các số tự nhiên

– Với số có 2 chữ số: gồm hàng chục, hàng đơn vị.

– Với số có 3 chữ số: gồm hàng trăm, hàng chục, hàng đơn vị.

– Với số có 4 chữ số: gồm hàng nghìn, hàng trăm, hàng chục, hàng đơn vị.

– Với số có 5 chữ số: gồm hàng chục nghìn, hàng nghìn, hàng trăm, hàng chục, hàng đơn vị.

– Phân tích số tự nhiên

Cho số tự nhiên có 4 chữ số abcd, ta có các cách phân tích phổ biến như sau:

• Phân tích theo các nghìn, các trăm, các chục, các đơn vị:

abcd = a000 + b00 + c0 + d

= a x 1000 + b x 100 + c x 10 + d

• Phân tích theo các nghìn và các đơn vị:

abcd = a000 + bcd

= a x 1000 + bcd

• Phân tích theo các trăm và các đơn vị:

abcd = ab00 + cd

= ab x 100 + cd

• Phân tích theo các chục và các đơn vị:

abcd = abc0 + d

= abc x 10 + d

♦ Lưu ý: Với các số có số lượng chữ số khác, cách phân tích hoàn toàn tương tự.

– Các dạng bài cấu tạo số thường gặp:

• Bài toán thay đổi vị trí các chữ số của một số tự nhiên.
• Bài toán thêm, bớt các chữ số ở bên trái, bên phải một số tự nhiên.
• Bài toán viết thêm các chữ số vào giữa một số tự nhiên.
• Bài toán về số tự nhiên và tổng các chữ số.
• Bài toán về tách tích (phép nhân) dựa trên cấu tạo.

– Phương pháp giải thông thường:

• Cách 1: Đưa bài toán về các dạng toán điển hình để giải.
• Cách 2: Dùng phân tích số để biến đổi mối quan hệ trong bài toán về các đẳng thức đơn giản để giải (thường chỉ đối với các bài toán cho biết số cần tìm có số lượng chữ số cụ thể).

2. Bài toán về dãy số lớp 5

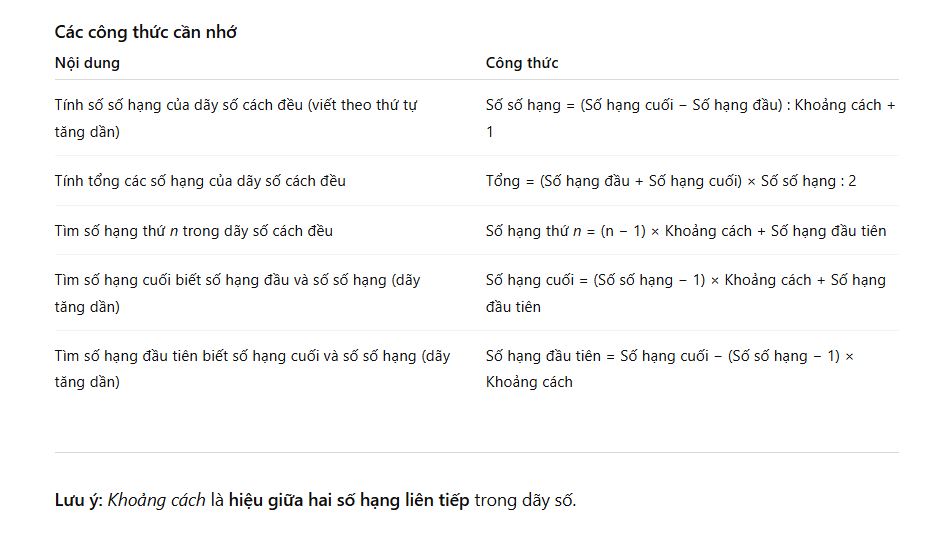
– Một số công thức liên quan đến dãy số cách đều:

• Tính số số hạng của dãy số cách đều(viết theo thứ tự tăng dần):

Số số hạng = (Số hạng cuối – Số hạng đầu) : Khoảng cách + 1

• Tính tổng các số hạng của dãy số cách đều:

Tổng các số hạng = (Số đầu + Số cuối) × Số số hạng : 2

• Tìm 1 số hạng biết số thứ tự của nó trong dãy số cách đều:

Số hạng thứ n = (n – 1) x Khoảng cách + Số hạng đầu tiên

• Tìm số cuối biết số hạng đầu tiên của nó trong dãy số cách đều (viết theo thứ tự tăng dần):

Số cuối = (Số số hạng – 1) × Khoảng cách + Số hạng đầu tiên

• Tìm số hạng đầu tiên biết số cuối của nó trong dãy số cách đều (viết theo thứ tự tăng dần):

Số hạng đầu tiên = Số cuối – (Số số hạng – 1) × Khoảng cách

♦ Lưu ý: “Khoảng cách” ở trên được hiểu là Khoảng cách giữa hai số hạng liên tiếp.

3. Bài toán về tính chẵn, lẻ, chữ số tận cùng

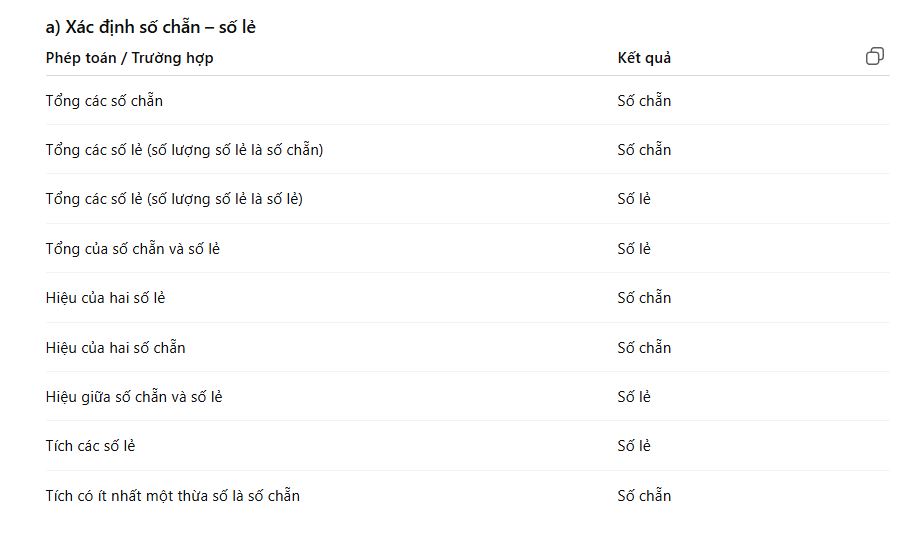
a) Xác định số chẵn, số lẻ

– Tổng các số chẵn là số chẵn.

– Tổng các số lẻ là:

• Số chẵn khi số lượng số lẻ là số chẵn.
• Số lẻ khi số lượng số lẻ là số lẻ.

– Tổng của số chẵn với số lẻ là số lẻ.

– Hiệu của hai số lẻ là số chẵn.

– Hiệu của hai số chẵn là số chẵn.

– Hiệu giữa số chẵn và số lẻ là số lẻ.

– Tích các số lẻ là số lẻ.

– Tích có một thừa số là số chẵn thì tích là số chẵn.

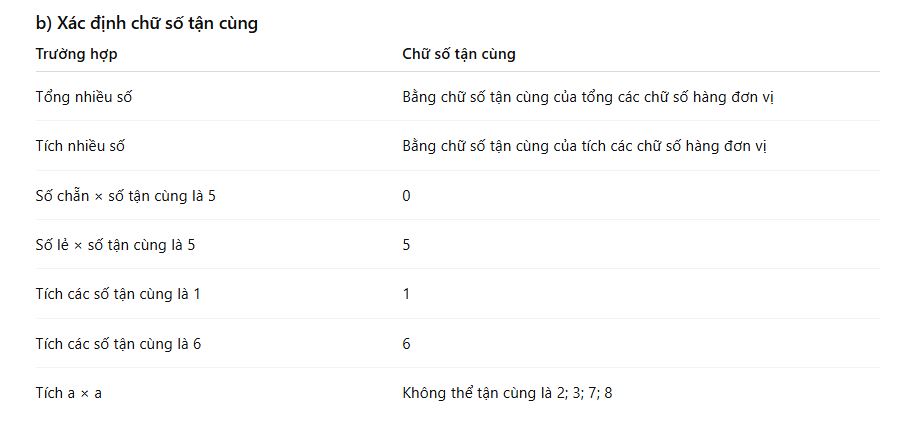
b) Xác định chữ số tận cùng

– Chữ số tận cùng của một tổng bằng chữ số tận cùng của tổng các chữ số hàng đơn vị của các số hạng trong tổng ấy.

– Chữ số tận cùng của một tích bằng chữ số tận cùng của tích các chữ số hàng đơn vị của các thừa số trong tích ấy.

• Tích một số chẵn với một số tận cùng là 5 thì tận cùng là 0.
• Tích một số lẻ với một số tận cùng là 5 thì tận cùng là 5.
• Tích các số tận cùng là 1 thì tận cùng là 1.
• Tích các số tận cùng là 6 thì tận cùng là 6.
• Tích a x a không thể tận cùng bằng 2; 3; 7 hoặc 8.

4. Bài toán tỉ lệ thuận – tỉ lệ nghịch

a) Bài toán tỉ lệ thuận

– Hai đại lượng gọi là tỉ lệ thuận nếu giá trị của đại lượng này tăng (hoặc giảm) bao nhiêu lần thì giá trị của đại lượng kia cũng tăng (hoặc giảm) bấy nhiêu lần.

♦ Phương pháp giải: Rút về đơn vị, lập tỉ số.

b) Bài toán tỉ lệ nghịch

– Hai đại lượng gọi là tỉ lệ nghịch nếu giá trị của đại lượng này tăng (hoặc giảm) bao nhiêu lần thì giá trị của đại lượng kia cũng giảm (hoặc tăng) bấy nhiêu lần.

♦ Phương pháp giải: Rút về đơn vị, lập tỉ số.

5. Bài tập về các phép toán phân số – Dãy phân số đặc biệt

5.1. Các phép toán về phân số

a) Phép cộng phân số

– Muốn cộng 2 phân số cùng mẫu số, ta cộng 2 tử số với nhau và giữ nguyên mẫu số.

– Muốn cộng 2 phân số khác mẫu số, ta quy đồng mẫu số 2 phân số rồi cộng 2 phân số đó.

Ví dụ:

3/9 + 2/9 = (3 + 2)/9 = 5/9

2/3 + ½ = 4/6 + 3/6 = (4 + 3)/6 = 7/6

Chú ý: Giống như phép cộng số tự nhiên, ta có tính chất giao hoán và tính chất kết hợp ở phép cộng phân số.

b) Phép trừ phân số

– Muốn trừ 2 phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số.

– Muốn trừ 2 phân số khác mẫu số, ta quy đồng mẫu số 2 phân số rồi trừ 2 phân số đó.

Ví dụ:

7/11 – 5/11 = (7 – 5)/11 = 2/11

3/5 – 1/3 = 9/15 – 5/15 = (9 – 5)/15 = 4/15

c) Phép nhân 2 phân số

– Muốn nhân 2 phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

Ví dụ:

3/5 x 2/7 = (3 x 2)/(5 x 7) = 6/35

Chú ý:

• Giống như phép nhân số tự nhiên, ở phép nhân phân số ta cũng có tính chất giao hoán, tính chất kết hợp, tính chất phân phối của phép nhân với phép cộng, tính chất phân phối của phép nhân với phép trừ.
• Khi thực hiện phép nhân các phân số, ta có thể giản ước các thừa số chung ở tử số và mẫu số, chứ không cần đợi đến khi nhân ra rồi mới rút gọn.

d) Phép chia 2 phân số

Để thực hiện phép chia 2 phân số, ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

Ví dụ:

2/3 : 5/11 = 2/3 x 11/5 = (2 x 11)/(3 x 5) = 22/15

1.2. Cách tính dãy phân số có quy luật

a) Dãy phân số có quy luật mẫu số sau gấp mẫu số trước 1 số không đổi

Đây là dạng toán liên quan đến tính tổng của một loạt các phân số mà mẫu số phân số sau gấp mẫu số phân số trước cùng 1 số lần. Ở dạng toán này chúng ta thường thực hiện theo các bước sau:

Giả sử tổng cần tìm là A.

• Bước 1: Phát hiện quy luật tử số của các phân số bằng nhau, mẫu số của phân số sau gấp mẫu số của phân số trước n lần.
• Bước 2: Tính A x n.
• Bước 3: Tính A x n – A. Từ đó rút ra A.

b) Dãy phân số có quy luật triệt tiêu lẫn nhau

Đây là dạng toán yêu cầu tính tổng một dãy các phân số có quy luật, mà quy luật ở mẫu số là tích các thừa số. Ở dạng toán này, chúng ta cần phân tích mẫu số thành các thừa số có quy luật nhất định, nhận xét được mối liên quan giữa tổng, hoặc hiệu các thừa số ở mẫu số và tử số.

• Bước 1: Phát hiện quy luật của mẫu số, tử số (thường sẽ là tích của các thừa số được lặp lại).

– Nếu đề bài chưa cho tích, ta hãy phân tích mẫu thành các tích.

– Nếu phân tích rồi mà chưa được, ta hãy nhân thêm 1 số nào đó để phân tích được thành có quy luật.

– Mẫu số của phân số này gấp bao nhiêu lần mẫu số của phân số trước?

• Bước 2: Nhận xét các thừa số ở mẫu:

– Hiệu các thừa số ở mẫu không thay đổi à dùng biến đổi: (b – a)/(a x b) = 1/a – 1/b. Sau khi biến đổi sẽ được các phân số có tử số bằng nhau, mẫu số có lặp lại và triệt tiêu lẫn nhau.

– Tổng các thừa số ở mẫu số bằng tử số à dùng biến đổi: (b + a)/(a x b) = 1/a + 1/b sẽ có dấu +, – xen kẽ, khi đó ta cũng triệt tiêu được các số giống nhau.

6. Bài toán lập số và quy tắc đếm

Với những bài toán không yêu cầu lập số cụ thể mà chỉ yêu cầu tìm ra số lượng các số thì ta có thể làm như sau:

+ Nếu trong mỗi số được lập các chữ số không phải khác nhau ta có cách tính số lượng số cần lập như sau:

• Có n chữ số sẽ có n cách chọn hàng cao nhất nếu n chữ số đó đều khác 0 và có n − 1 cách chọn hàng cao nhất nếu trong n chữ số đó có 1 chữ số bằng 0.
• Với mỗi cách chọn hàng cao nhất có n cách chọn hàng cao thứ nhì.
• Với mỗi cách chọn hàng cao thứ nhì thì có n cách chọn hàng cao thứ ba.
• Tương tự ta có n cách chọn cho hàng tiếp theo.

⇒  Số lượng số cần lập bằng tích của các cách chọn ở từng bước trên.

+ Nếu trong mỗi số được lập các chữ số phải khác nhau (các chữ số không lặp lại) ta có cách tính số lượng số cần lập như sau:

• Có n chữ số sẽ có n cách chọn hàng cao nhất nếu n chữ số đó đều khác 0 và có n − 1 cách chọn hàng cao nhất nếu trong n chữ số đó có 1 chữ số bằng 0.
• Với mỗi cách chọn hàng cao nhất có n – 1 cách chọn hàng cao thứ nhì.
• Với mỗi cách chọn hàng cao thứ nhì thì có n – 2 cách chọn hàng cao thứ ba.
• Cứ tiếp tục như thế cho đến khi lập được số thoả mãn yêu cầu.

⇒ Số lượng số cần lập bằng tích của các cách chọn ở từng bước trên.

♦ Ghi nhớ: Trong trường hợp xét số cách chọn của chữ số hàng đơn vị mà có xuất hiện chữ số 0 thì ta phải chia 2 trường hợp:

• Trường hợp 1: Hàng đơn vị bằng 0.
• Trường hợp 2: Hàng đơn vị khác 0.

7. Các bài toán liên quan đến tỉ số lớp 5

7.1. Các bài toán cơ bản về tỉ số lớp 5

a) Tìm tỉ số của hai số

Muốn tìm tỉ số của hai số ta tìm thương của hai số rồi viết dưới dạng phân số.

b) Tìm giá trị phân số của một số cho trước

Muốn tìm a/b của số M, ta lấy M x a/b hay M nhân với a rồi chia cho b hoặc lấy M chia cho b rồi nhân với a.

c) Tìm một số biết a/b của số đó bằng m

Để tìm một số biết a/b của số đó bằng mta lấy m : a/b hay m chia cho a rồi nhân với b.

7.2. Bài toán “Hai tỉ số”

a) Dạng bài

Trong bài toán tìm 2 số khi biết 2 tỉ số, ta thường gặp hoặc biến đổi để đưa về các dạng sau: Hai tỉ số có tổng không đổi, hai tỉ số có hiệu không đổi hoặc đơn giản hơn là 1 trong 2 đại lượng của đề bài là đại lượng không đổi.

Khi đó, ta lấy đại lượng không đổi làm đơn vị để tính toán, so sánh.

b) Phương pháp giải

Trong bài toán hai tỉ số có 2 thành phần A và B.

+ Bước 1: Xác định đại lượng nào của bài toán là không đổi: Tổng của A và B, hiệu của A và B hay là chính 1 trong 2 thành phần A hoặc B.

+ Bước 2: So sánh tỉ số của A (hoặc B) với đại lượng không đổi đã tìm ở bước 1.

+ Bước 3: Tính xem lượng thêm hoặc bớt ở A (hoặc B) ứng với bao nhiêu phần của đại lượng không đổi, từ đó tìm ra đại lượng không đổi rồi đưa về bài toán cơ bản.

8. Các bài toán về tổng – tỉ, hiệu – tỉ

a) Bài toán tìm hai số khi biết tổng và tỉ số của chúng

+ Cách giải chung

– Bước 1: Vẽ sơ đồ đoạn thẳng biểu diễn cho hai số theo dữ kiện để bài ra. (Học sinh có thể lược bớt bước vẽ sơ đó và chỉ cần chỉ ra được số phần bằng nhau biểu thị hai số)

– Bước 2: Tìm tổng số phần bằng nhau.

– Bước 3: Tìm số bé và số lớn (Có thể tìm số bé trước hoặc tìm số lớn trước)

Số bé = (Tổng: Tổng số phần bằng nhau) × Số phần của số bé (hoặc Số bé = Tổng – Số lớn)

Số lớn = (Tổng : Tổng số phần bằng nhau) × Số phần của số lớn (hoặc Số lớn = Tổng – Số bé)

– Bước 4: Kết luận đáp số.

b) Bài toán tìm hai số khi biết hiệu và tỉ số của chúng

+ Cách giải chung

– Bước 1: Vẽ sơ đồ đoạn thẳng biểu diễn cho hai số theo dữ kiện đề bài ra.

– Bước 2: Tìm hiệu số phần bằng nhau.

– Bước 3: Tìm số bé và số lớn (Có thể tìm số bé trước hoặc tìm số lớn trước)

Số bé = (Hiệu : Hiệu số phần bằng nhau) × Số phần của số bé (hoặc Số bé = Số lớn – Hiệu)

Số lớn = (Hiệu : Hiệu số phần bằng nhau) × Số phần của số lớn (hoặc Số lớn = Số bé + Hiệu)

– Bước 4: Kết luận đáp số.

♦ Lưu ý: Trong một số bài toán, tổng (hiệu) số hoặc tỉ số không được cho trước. Chúng ta cần phải đi tìm tổng (hiệu) số hoặc tỉ số trước rồi tiếp tục làm theo các bước như trên.

9. Các bài toán về số thập phân

9.1. Các tính chất của phép tính

a) Tính chất:

Các tính chất trong phép cộng, trừ, nhân, chia số thập phân cũng tương tự như các tính chất trong cộng, trừ, nhân, chia số tự nhiên (giao hoán, kết hợp, quy tắc dấu ngoặc, …).

b) Quy tắc nhân, chia nhẩm:

– Muốn nhân một số thập phân với 10; 100; 1000; … ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, … chữ số.

– Muốn chia một số thập phân cho 10; 100; 1000; … ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.

– Muốn nhân một số thập phân với 0,1; 0,01; 0,001; … ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.

– Muốn chia một số thập phân cho 0,1; 0,01; 0,001; … ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, … chữ số.

– Muốn nhân một số với 0,5 ta chia số đó cho 2.

– Muốn chia một số cho 0,5 ta nhân số đó với 2.

– Muốn nhân một số với 0,25 ta chia số đó cho 4.

– Muốn chia một số cho 0,25 ta nhân số đó với 4.

– Muốn nhân một số với 0,125 ta chia số đó cho 8.

– Muốn chia một số cho 0,125 ta nhân số đó với 8.

1.2. Mối quan hệ giữa các thành phần của phép tính

a) Phép cộng – phép trừ:

• Trong 1 tổng, nếu thêm (bớt) 1 số hạng của tổng bao nhiêu đơn vị thì tổng cũng thêm (bớt) bấy nhiêu đơn vị.
• Trong 1 hiệu, nếu thêm (bớt) số bị trừ bao nhiêu đơn vị thì hiệu cũng thêm (bớt) bấy nhiêu đơn vị.
• Trong 1 hiệu, nếu thêm (bớt) số trừ bao nhiêu đơn vị thì hiệu cũng bớt (thêm) bấy nhiêu đơn vị

b) Phép nhân – phép chia

• Trong 1 tích, nếu gấp lên (giảm đi) 1 thừa số bao nhiêu lần thì tích cũng gấp lên (giảm đi) bấy nhiêu lần.
• Trong phép chia hết, nếu số bị chia gấp lên (giảm đi) bao nhiêu lần thì thương cũng gấp lên (giảm đi) bấy nhiêu lần.
• Trong phép chia hết, nếu số chia gấp lên (giảm đi) bao nhiêu lần thì thương giảm đi (gấp lên) bấy nhiêu lần.

10. Các bài toán về tỉ số phần trăm

a) Dạng 1: Tìm tỉ số phần trăm của 2 số

– Muốn tìm tỉ số phần trăm của hai số a và b, ta làm như sau:

• Tìm thương của a và b.
• Nhân thương đó với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.

b) Dạng 2: Tìm giá trị phần trăm của một số cho trước

Muốn tìm n% của số A, ta lấy A nhân với n% hay lấy A nhân với n/100.

c) Dạng 3: Tìm một số biết một giá trị phần trăm của số đó

Tìm một số biết n% của số đó bằng A, ta lấy A chia n% hay lấy A chia cho n/100.

11. Bài toán về diện tích tam giác – Hình thang

a) Một số công thức cơ bản

• Muốn tính diện tích tam giác, ta lấy độ dài đáy nhân với chiều cao tương ứng (cùng đơn vị đo) rồi chia cho 2.
• Muốn tính diện tích hình thang, ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2 hay lấy trung bình cộng độ dài hai đáy nhân với chiều cao.

♦ Lưu ý: Trong hình tam giác:

• Muốn tính độ dài đáy, ta lấy diện tích nhân với 2 rồi chia cho chiều cao tương ứng.
• Muốn tính chiều cao, ta lấy diện tích nhân với 2 rồi chia cho độ dài đáy tương ứng.

b) Một số tính chất

• Với hai tam giác có chung đáy hoặc đáy bằng nhau thì tỉ số diện tích bằng tỉ số các chiều cao tương ứng.
• Với hai tam giác có chung chiều cao hoặc chiều cao bằng nhau thì tỉ số diện tích bằng tỉ số độ dài các đáy tương ứng.
• Trong một hình thang ta có thể kẻ được nhiều đường cao, nhưng mọi đường cao trong hình thang đều có độ dài bằng nhau.

12. Bài toán về hình tròn và hình khối hộp

a) Một số công thức cơ bản

1.1. Một số công thức cơ bản về tính diện tích, thể tích

a) Hình tròn

Cho hình tròn có bán kính r. Khi đó:

– Đường kính hình tròn:

d = 2 × r

– Diện tích hình tròn:

S = 3,14 × r × r

– Chu vi hình tròn:

C = 3,14 × d hoặc C = 3,14 × 2 × r

b) Hình khối hộp

+ Hình hộp chữ nhật

– Diện tích xung quanh của hình hộp chữ nhật (kí hiệu Sxq) à tổng diện tích bốn mặt bên:

Sxq = Chu vi đáy x Chiều cao = (Chiều dài + Chiều rộng) x 2 x Chiều cao

– Diện tích toàn phần của hình hộp chữ nhật (kí hiệu Stp) là tổng của diện tích xung quanh và diện tích hai đáy:

Stp = Sxq + S2 đáy = (Chiều dài + Chiều rộng) x 2 x Chiều cao + Chiều dài x Chiều rộng x 2

– Thể tích hình hộp chữ nhật (kí hiệu V):

V = Chiều dài x Chiều rộng x Chiều cao

Hoặc

V = Sđáy x Chiều cao

+ Hình lập phương

• Hình lập phương có sáu mặt là các hình vuông bằng nhau.
• Hình lập phương là hình hộp chữ nhật đặc biệt.

– Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân với 4:

Sxq = S1 mặt x 4 = Cạnh x Cạnh x 4

– Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân với 6:

Stp = Cạnh × Cạnh × 6 = Cạnh × Cạnh × 6

– Thể tích hình lập phương bằng cạnh nhân cạnh nhân cạnh:

V = Cạnh × Cạnh × Cạnh

1.2. Một số công thức về hình hộp chữ nhật, hình lập phương liên quan tìm số khối được sơn đúng 1 mặt, 2 mặt, 3 mặt, không được sơn mặt nào

Xếp các khối lập phương đơn vị (khối lập phương nhỏ có cạnh là 1 đơn vị độ dài) thành một hình hộp chữ nhật (hoặc hình lập phương) lớn có chiều dài, chiều rộng, chiều cao lần lượt là a; b; c rồi sơn 6 mặt của hình hộp chữ nhật lớn thì ta có:

• Các khối nhỏ được sơn 3 mặt là các khối nằm ở đỉnh hình hộp chữ nhật lớn. Có 8 đỉnh nên có 8 khối nhỏ được sơn 3 mặt.
• Các khối nhỏ được sơn đúng 2 mặt là các khối nằm ở cạnh nhưng không nằm ở đỉnh của hình hộp chữ nhật lớn.

– Hình hộp chữ nhật lớn có 4 cạnh dài, 4 cạnh rộng và 4 cạnh cao nên có số khối nhỏ được sơn đúng 2 mặt là:

(a – 2) x 4 + (b – 2) x 4 + (c – 2) × 4

– Nếu hình lớn được xếp thành là hình lập phương cạnh a thì có số khối nhỏ được sơn đúng 2 mặt là:

(a – 2) × 12

– Các khối nhỏ được sơn đúng 1 mặt là các khối nằm ở mặt nhưng không nằm ở cạnh của hình hộp chữ nhật lớn.

– Có 2 mặt đáy hình chữ nhật chứa chiều dài, chiều rộng; 2 mặt bên hình chữ nhật chứa chiều dài, chiều cao; 2 mặt bên hình chữ nhật chứa chiều rộng chiều cao nên có số khối nhỏ được sơn đúng 1 mặt là:

(a – 2) x (b – 2) x 2 + (a – 2) x (c – 2) x 2 + (b – 2) x (c – 2) × 2

– Nếu hình lớn được xếp thành là hình lập phương cạnh a thì có số khối nhỏ được sơn đúng 1 mặt là:

(a – 2) × (a – 2) × 6

– Các khối lập phương nhỏ không được sơn mặt nào xếp thành hình hộp chữ nhật có kích thước là:

a – 2; b – 2; c – 2

– Có (a − 2) × (b − 2) × (c – 2) khối nhỏ không được sơn mặt nào.

– Nếu hình lớn được xếp thành là hình lập phương cạnh a thì có số khối nhỏ không được sơn mặt nào là:

(a – 2) × (a – 2) × (a − 2)

13. Bài toán chuyển động lớp 5

Hy vọng phần tổng hợp các bài toán lớp 5 kèm hướng dẫn giải chi tiết từng dạng toán ở trên đã giúp các em nắm vững kiến thức trọng tâm, hiểu rõ phương pháp giải và tránh được những lỗi sai thường gặp.

Để luyện tập thêm nhiều bài toán hay và đa dạng mức độ, phụ huynh và học sinh có thể tham khảo cuốn 250+ bài toán chọn lọc lớp 5  của TKbooks với hệ thống bài tập chọn lọc, bám sát chương trình và có hướng dẫn giải chi tiết.

Link đọc thử sách: https://drive.google.com/file/d/1EnnjMiJ4MNEGPFR-Ar9WSRiPIzcLcBaQ/view

Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 5 hàng đầu tại Việt Nam!

TKbooks.vn