Chưa có sản phẩm trong giỏ hàng.
Tích vô hướng của hai vectơ và ứng dụng trong tính diện tích tam giác
Tích vô hướng của hai vectơ là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.
Dưới đây là toàn bộ kiến thức về tích vô hướng của hai vectơ. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KỲ (TỪ 0o ĐẾN 180°)
1. Định nghĩa
Với mỗi góc a (0° < a < 180°) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho ↷xOM = α và giả sử điểm M có tọa độ M(X0;Y0).
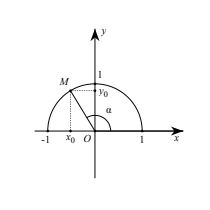
Khi đó ta có định nghĩa:
sin của góc α là y0, kí hiệu sin α = y0.
cosin của góc α là x0 , kí hiệu cos α = x0 .
tang của góc α là y0/x0 (x0 ≠0), kí hiệu tan α = y0/x0
cotang của góc α là x0/y0 (y0≠0), kí hiệu cot α = x0/y0
2. Tính chất
Trên hình bên ta có dây cung NM song song với trục Ox và nếu ↷xOM = α thì ↷xON =180° – α.
Ta có yM = yN = y0, xM = – xN = x0
Do đó:
sin α = sin (180° – α)
cos α = – cos(180° – α)
tan α = – tan (180° – α)
cot a = – cot (180° – α)
Ví dụ: cos135° = – cos(180° – 45°) = – cos 45° = – √2/2
3. Góc giữa hai vectơ
a) Định nghĩa
Cho hai vectơ →a và →b đều khác vectơ →0 . Từ một điểm 0 bất kì ta vẽ →OA = →a và →→OB = →b . Góc ↷AOB với số đo từ 0° đến 180° được gọi là góc giữa hai vectơ →a và →b . Ta kí hiệu góc giữa hai vectơ →a và →b là (→a, →b) . Nếu (→a, →b) = 90° thì ta nói rằng →a và →b vuông góc với nhau, kí hiệu là →a ∟→b hoặc →b ∟→a.
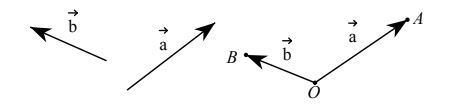
b) Chú ý
Từ định nghĩa ta có (→a, →b) = (→b, →a).
II. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
1. Định nghĩa tích vô hướng của hai vectơ
Cho hai vectơ →a và →b đều khác vectơ 0 . Tích vô hướng của→ a và →b là một số, kí hiệu là →ab, được xác định bởi công thức sau:
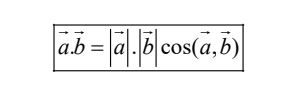
Trường hợp ít nhất một trong hai vectơ →a và →b bằng vectơ 0 ta quy ước →a. →b = 0.
Chú ý:
- Với →a và →b khác vectơ 0 ta có →a. →b = →a ∟ →b
- Khi →a = →b tích vô hướng →a. →a được kí hiệu là →a2 và số này được gọi là bình phương vô hướng của vectơ →a.
Ta có:
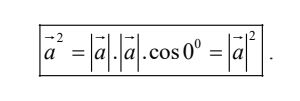

2. Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng:
Với ba vectơ →a, →b, →c bất kì và mọi số k ta có:
→a. →b = →b. →a (tính chất giao hoán);
→a(→b + →c) = →a. →b + →a. →c (tính chất phân phối);
(k. →a). →b = k(→a. →b) = →a.(k. →b);
→a2 ≥0, →a = 0⟺ →a = 0
Nhận xét: Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
(→a + →b)² = →a² + 2→a. →b + →b²
(→a – →b)² = →a² – 2→a. →b + →b²
(→a + →b)( →a – (→b)) = →a².→b².

3. Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ (O;i; j), cho hai vectơ →a=(a1;a,), →b = (b;b, ) . Khi đó tích vô hướng ab là:
→a.→b= a1b1 + a₂b₂
Nhận xét: Hai vectơ →a = (a,;a,), →b = (b;b,) đều khác vectơ 0 vuông góc với nhau khi và chỉ khi a1b1 + a₂b₂ = 0.

4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ →a = (a,;a,) được tính theo công thức:
b) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu →a = (a,;a,) và →b = (b;b,) đều khác 0 thì ta có:
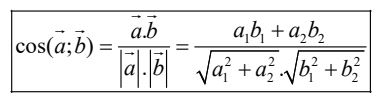
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm A(xA;yA) và B(xB;yB) được tính theo công thức:
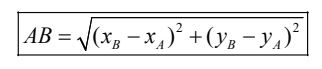
III. CÁC HỆ THÚC LƯỢNG TRONG TAM GIÁC VÀ GIẢI TAM GIÁC
1. Định lí côsin
Cho tam giác ABC có BC = a, AC = b và AB = c
Ta có:
a² = b² + c² – 2bc.cos A
b² = c² + a² – 2ca.cos B
c² = a² + b² – 2ab.cos C
Hệ quả:
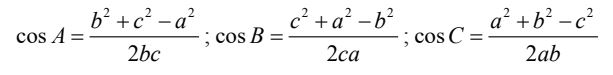
2. Định lí sin
Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.
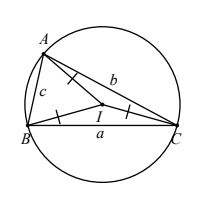
Ta có:
a/sin A = b/sin B = c/sin C = 2R.
3. Độ dài đường trung tuyến
Cho tam giác ABC có ma, mb, mc lần lượt là các trung tuyến kẻ từ A, B, C.
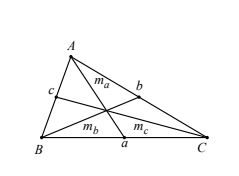
Ta có:
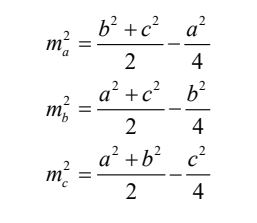
4. Độ dài đường phân giác
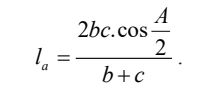
5. Công thức tính diện tích tam giác
Cho tam giác ABC có ha, hb, hc lần lượt tương ứng với các cạnh BC, CA, AB;
R là bán kính đường tròn ngoại tiếp tam giác;
r là bán kính đường tròn nội tiếp tam giác;
p = (a + b + c)/2là nửa chu vi tam giác;
S là diện tích tam giác.
Khi đó ta có:
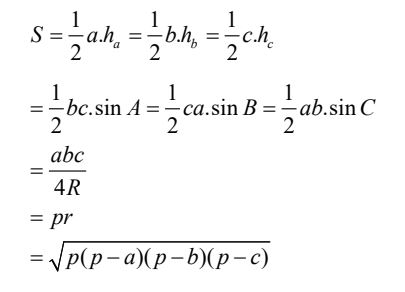
6. Một số công thức khác cho ΔABC
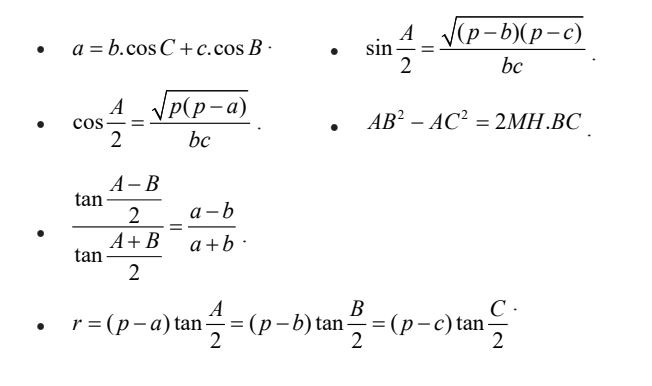
V. Một số bài tập về tích vô hướng của hai vectơ
Dưới đây là một số dạng toán cơ bản về Cung và góc lượng giác để các em luyện tập và ôn luyện kiến thức:


Các dạng toán khác về Tích vô hướng của hai vectơ và ứng dụng được ghi chú và diễn giải rất đầy đủ trong cuốn cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.


