Chưa có sản phẩm trong giỏ hàng.
Tam giác đồng dạng lớp 8 – Lý thuyết và các định lí cần nhớ
Trong bài viết Tam giác đồng dạng lớp 8 – Lý thuyết và các định lí cần nhớ dưới đây, chúng ta sẽ cùng nhau khám phá những định nghĩa cơ bản, các tiêu chí để xác định hai tam giác có đồng dạng với nhau hay không, và cách áp dụng các tiêu chí đó vào giải toán thực tế.
Mời các em tham khảo!
1. Tam giác đồng dạng là gì?
Hai tam giác được gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau đôi một và ba cặp cạnh tương ứng tỉ lệ.
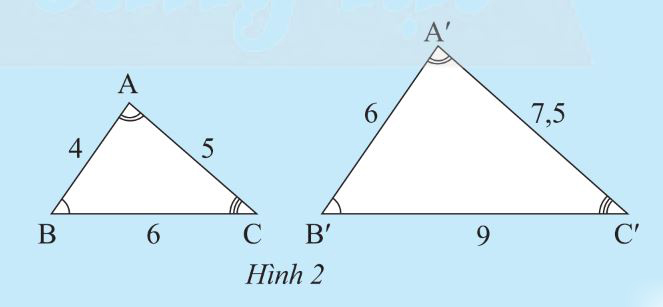
Ví dụ. Tam giác ABC và tam giác A’B’C’ có:
Góc A = góc A’, góc B = góc B’, góc C = góc C’
AB/ A’B’ = BC/B’C’ = CA/C’A’ ó △ABC ∼ △A’B’C’
- Các góc bằng nhau gọi là các góc tương ứng.
- Các đỉnh của các góc bằng nhau gọi là các đỉnh tương ứng.
- Các cạnh đối diện với góc bằng nhau gọi là các cạnh tương ứng.
- Khi dùng kí hiệu △ABC ∼ △A’B’C’ thì phải ghi đúng thứ tự cặp đỉnh tương ứng.
- Tỉ số của hai cạnh tương ứng k gọi là tỉ số đồng dạng.
2. Tính chất của tam giác đồng dạng
a) Mỗi tam giác đồng dạng với chính tam giác đó (hoặc Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Nếu △ABC ∼ △A’B’C’ theo tỉ số k thì △A’B’C’ ∼ △ABC theo tỉ số 1/k.
Nếu △ABC ∼ △A’B’C’ và △A’B’C’ ∼ △A”B”C” thì △ABC ∼ △A”B”C”.
Lưu ý. Nếu △ABC và △A’B’C’ đồng dạng theo tỉ số k1, △A’B’C’ và △A”B”C” đồng dạng theo tỉ số k2, thì △ABC và △A”B”C” đồng dạng theo tỉ số k1.k2.
3 . Định lí về tam giác đồng dạng
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác đồng dạng với tam giác đã cho.
4. Các trường hợp đồng dạng của hai tam giác
a. Trường hợp đồng dạng thứ nhất cạnh – cạnh – cạnh (c.c.c).
Định lí. Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Ví dụ. Xét tam giác ABC và tam giác A’B’C’ có AB/A’B’ = BC/B’C’ = CA/C’A’ thì △ABC ∼ △A’B’C'(c.c.c).
Nhận xét. Hai tam giác đều bất kì luôn đồng dạng với nhau (c.c.c).

b. Trường hợp đồng dạng thứ hai cạnh – góc – cạnh (c.g.c)
Định lí. Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
Ví dụ. Xét tam giác △ABC và △A’B’C’ có:
Góc A = góc A’ và AB/A’B’ = AC/A’C’ thì △ABC ∼ △A’B’C’ (c.g.c).
Nhận xét.
- Hai tam giác vuông bất kì luôn đồng dạng với nhau (c.g.c)
- Nếu góc ở đỉnh của tam giác cân này bằng góc ở đỉnh của tam giác cân kia thì hai tam giác cân đó đồng dạng với nhau (c.g.c).
c. Trường hợp đồng dạng thứ ba góc – góc (g.g)
Định lí. Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau (g.g).
Ví dụ. Xét tam giác △ABC và △A’B’C’ có góc A = góc A’ và góc B = góc B’ thì △ABC ∼ △A’B’C'(g.g).
Nhận xét. Nếu góc ở đáy của tam giác cân này bằng góc ở đáy của tam giác cân kia thì hai tam giác cân đó đồng dạng với nhau (g.g).
5. Các trường hợp đồng dạng của tam giác vuông
+ Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông
- Hai tam giác vuông đồng dạng với nhau nếu:
- Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia (trường hợp đồng dạng thứ ba – g.g).
- Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia (trường hợp đồng dạng thứ hai – c.g.c).
+ Dấu hiệu đặc biệt nhận biết hai tam giác vuông đồng dạng
- Định lí 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng (trường hợp cạnh huyền – cạnh góc vuông).
+ Tỉ số đường cao, đường trung tuyến, đường phân giác, tỉ số diện tích của hai tam giác vuông đồng dạng.
- Định lí 2: Tỉ số hai đường cao tương ứng của hai tam giác vuông đồng dạng là bằng tỉ số đồng dạng.
- Định lí 3: Tỉ số hai đường trung tuyến tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Định lí 4: Tỉ số hai đường phân giác tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Định lí 5: Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Hi vọng bài viết Tam giác đồng dạng lớp 8 – Lý thuyết và các định lí cần nhớ ở trên sẽ trang bị cho các bạn học sinh các công cụ cần thiết để nhận biết và chứng minh sự đồng dạng giữa các tam giác, qua đó giúp các em tiếp cận và giải quyết các bài tập liên quan một cách hiệu quả.
Để xem thêm lý thuyết và các dạng bài tập về tam giác đồng dạng lớp 8, các em có thể tham khảo thêm cuốn sách Làm chủ kiến thức Toán lớp 8 Phần Hình học.
Link đọc thử sách: https://drive.google.com/file/d/1NhDosmt57ti_t4iZYGXd5evVCVB2bf2M/view
Chúc các em làm tốt các bài kiểm tra và bài tập về tam giác đồng dạng sắp tới nhé!


