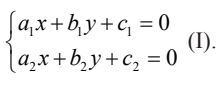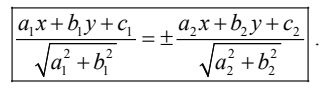Phương pháp tọa độ trong mặt phẳng – Lý thuyết, bài tập và cách giải
Phương pháp tọa độ trong mặt phẳng là kiến thức quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 5% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.
Dưới đây là toàn bộ kiến thức về Phương pháp tọa độ trong mặt phẳng. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
I. PHƯƠNG TRÌNH ĐƯỜNG THẲNG
1. Vectơ chỉ phương của đường thẳng
Vectơ →u được gọi là VTCP của đường thẳng A nếu →u ≠ 0 và giá của →u song song hoặc trùng với A.
Nhận xét: Một đường thẳng có vô số VTCP.

2. Phương trình tham số của đường thẳng
Phương trình tham số của đường thẳng Δ:
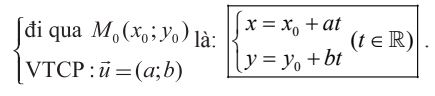
Nhận xét: Nếu đường thẳng Δ có VTCP →u = (a;b) thì có hệ số góc k = b/a.

3. Phương trình chính tắc của đường thẳng
Phương trình chính tắc của đường thẳng Δ:
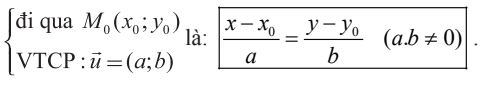
4. Vectơ pháp tuyến của đường thẳng
Vectơ →n được gọi là VTPT của đường thẳng Δ nếu n ≠ 0 và →n vuông góc với VTCP của Δ.
Nhận xét:
- Một đường thẳng có vô số VTPT.
- Mối quan hệ giữa VTCP và VTPT
→u = (a;b) => →n = (b;-a)
→n = (A;B) => →u = (B;-A)
5. Phương trình tổng quát của đường thẳng
Phương trình tổng quát của đường thẳng Δ:
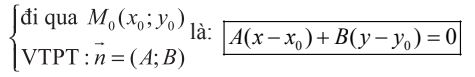
hay Ax + By + C = 0 với C = -Ax0 – By0
Nhận xét:
- Nếu đường thẳng Δ có VTPT →n = (A;B) thì có hệ số góc k = -A/B
- Nếu A, B, C đều khác 0 thì ta có thể đưa phương trình tổng quát về dạng x/a0 + y/b0 = 1 với a0 = – C/A, b0 = – C/B.
Phương trình này được gọi là phương trình đường thẳng theo đoạn chắn, đường thẳng này cắt Ox và Oy lần lượt tại M(a0;0) và N(0;b0).

Các phương trình đường thẳng đặc biệt:
| Δ ≡ Ox | Δ // Ox | Δ ≡Oy | Δ // Oy | |
| PT tổng quát | y = 0 | y = m | x = 0 | x = m |
| PT tham số | {x=ty=0 | {x=ty=m | {x=0y=t | {x=ny=t |
6. Vị trí tương đối của hai đường thẳng
Cho hai đường thẳng có phương trình tổng quát là Δ1 = a1x + b1y + c = 0 và Δ2 = a2x + b2y + c = 0
- Cách 1: Xét tọa độ giao điểm của Δ1 và Δ2 (nếu có) là nghiệm của hệ phương trình:
| Số nghiệm của hệ (I) | Hệ quả |
| 0 | Δ1 // Δ2 |
| 1 | Δ1 ∩ Δ2 |
| Vô số | Δ1 ≡ Δ2 |
- Cách 2: Xét tỉ số (nếu a,.b,.c, ≠ 0)
| Điều kiện | Hệ quả |
| a1/a2 = b1/b2 = c1/c2 | Δ1 ≡ Δ2 |
| a1/a2 = b1/b2 ≠ c1/c2 | Δ1 // Δ2 |
| a1/a2 ≠ b1/b2 | Δ1 ∩ Δ2 ⊥ |
| a1.a2 + b1.b2 = 0 | Δ1 ⊥ Δ2 |
7. Vị trí tương đối của hai điểm đối với một đường thẳng
Cho đường thẳng Δ : ax + by + c = 0 và hai điểm M(xM,yM ) ∉ Δ, N(xN, yN) ∉ Δ.
- M, N nằm cùng phía đối với Δ khi và chỉ khi
| (a..xM + b.yM + c)(a.xN + b.yN + c) > 0 |
- M, N nằm khác phía đối với Δ khi và chỉ khi
| (a..xM + b.yM + c)(a.xN + b.yN + c) < 0 |
8. Góc giữa hai đường thẳng
Cho hai đường thẳng:
- Δ1 = a1x + b1y + c = 0 có VTPT →n1(a1; b1), VTCP u1(b1;-a1)
- Δ2 = a2x + b2y + c = 0 có VTPT →n2(a2; b2), VTCP u1(b2;-a2)
Gọi α là góc tạo bởi hai đường thẳng Δ1 và Δ2.
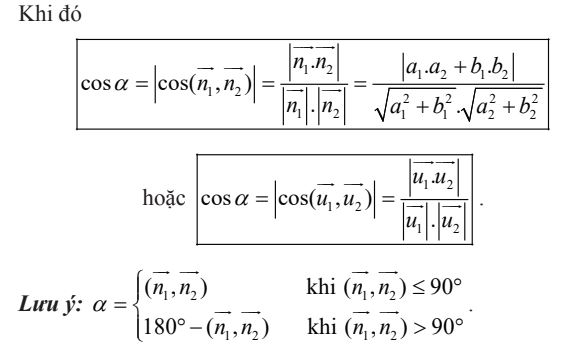

9. Khoảng cách từ một điểm đến một đường thẳng
Khoảng cách từ M (xM;yM) đến đường thẳng Δ : ax + by + c = 0 được tính theo công thức:
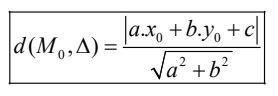
Nhận xét: Cho hai đường thẳng Δ1 = a1x + b1y + c = 0 và Δ2 = a2x + b2y + c = 0 cắt nhau thì phương trình hai đường phân giác của góc tạo bởi hai đường thăng trên là:
Lưu ý: Để lập phương trình đường phân giác trong hoặc ngoài của góc A trong tam giác ABC ta có thể thực hiện như sau:
- Viết phương trình các đường phân giác A,A, của các góc tạo bởi hai đường thăng AB, AC
- Kiểm tra vị trí của hai điểm B, C đối với A, (hoặc A, ).
+ Nếu B, C nằm khác phía đối với A, thì A, là đường phân giác trong.
+ Nếu B, C năm cùng phía đối với A, thì A, là đường phân giác ngoài

II. ĐƯỜNG TRÒN
1. Phương trình đường tròn có tâm và bán kính cho trước
Trong mặt phẳng Oxy, đường tròn (C) tâm I(a;b), bán kính R có phương trình:
| (x − a)² + (y − b)² = R² |
Hoặc
| x² + y² – 2ax – 2by + c = 0 |
trong đó c = a2 + b2 – R2
2. Nhận xét
Phương trình
| x² + y² – 2ax – 2by + c = 0 |
là phương trình của trình đường tròn (C) khi a2 + b2 – c > 0.
Khi đó, bán kính là: R = √(a2 + b2 – c)
3. Phương trình tiếp tuyến của đường tròn
Cho đường tròn (C) có tâm I(a;b), bán kính R và đường thẳng Δ.
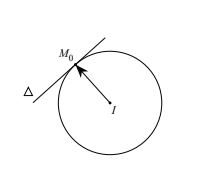
Δ tiếp xúc với (C) = d(I, Δ) = R
- Dạng 1: Tiếp tuyến tại một điểm M (x0;y0)∈(C).
Δ đi qua M (x0;y0) và có VTPT →IM0
hay có dạng:
| (x0 − a)(x − x0) + (y0 − b)(y − y0) = 0 |
- Dạng 2: Tiếp tuyến có phương cho trước.
+ B1: Viết phương trình của Δ có phương cho trước (phương trình chứa tham số t).
+ B2: Dựa vào điều kiện: d(I,Δ) = R, ta tìm được t . Từ đó suy ra phương trình của Δ.
- Dạng 3: Tiếp tuyến vẽ từ một điểm A(xA;yA) ở ngoài đường tròn (C).
+ B1: Viết phương trình của Δ đi qua A (chứa 2 tham số).
+ B2: Dựa vào điều kiện: d(I,Δ)= R , ta tìm được các tham số.
Từ đó suy ra phương trình của Δ.
4. Phương trình đường thẳng đi qua 2 tiếp điểm
Cho M (xM;yM) nằm ngoài đường tròn tâm I(a;b) bán kính R.
Từ M dựng 2 tiếp tuyến tiếp xúc đường tròn tại 2 điểm A, B.
Phương trình đường thẳng AB có dạng:
| (x − a)( xM − a) + (y – b)(yM – b) = R² |
5. Vị trí tương đối của đường thẳng và đường tròn
Gọi d là khoảng cách từ tâm O của đường tròn (C) đến đường thẳng Δ, ta có:
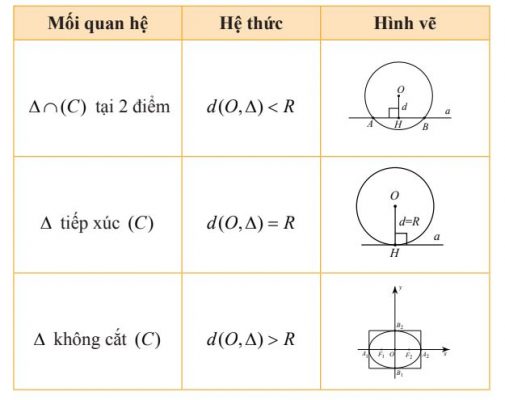
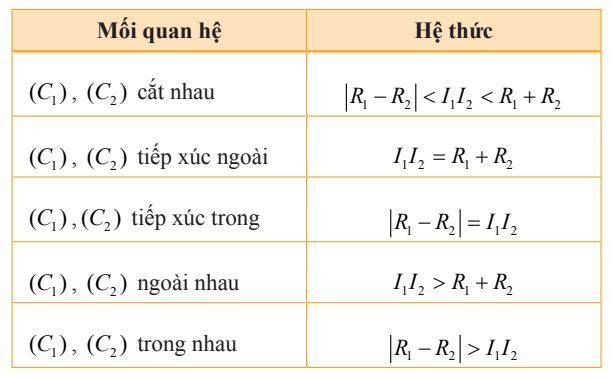
6. Vị trí tương đối của hai đường tròn
Cho (C): x² + y² −2a₁x − 2b₁y + c₁ = 0
(C2): x² + y² −2a2x − 2b2y + c2 = 0
III. ĐƯỜNG ELIP
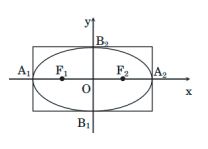
1. Định nghĩa
Cho hai điểm cố định F1 và F2 với F1. F2 = 2c (c > 0). Tập hợp các điểm M thỏa mãn MF1 + MF2 = 2a (a không đổi và a > c > 0) là một đường Elip.
- F1, F2 là hai tiêu điểm.
- F F2 = 2c là tiêu cự của Elip.
2. Phương trình chính tắc của Elip
(E) : x2/a2 + y2/b2 = 1 (với a2 + b2 = c2)
Điểm M(xM;yM)∈(E) ⟺ xM2/a2 + yM2/b2 = 1 và |xM| ≤ a, |yM| ≤ b.
3. Tính chất và hình dạng của Elip
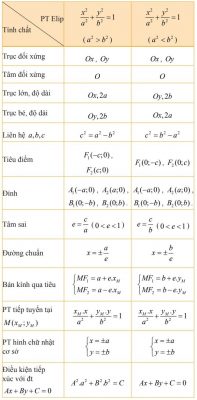
IV. Bài tập về phương pháp tọa độ trong mặt phẳng
Dưới đây là một số dạng toán cơ bản về Phương pháp tọa độ trong mặt phẳng để các em luyện tập:

Các dạng toán khác về Phương pháp tọa độ trong mặt phẳng được ghi chú và diễn giải rất đầy đủ trong cuốn cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.