Chưa có sản phẩm trong giỏ hàng.
Phép cộng trừ các số nguyên lớp 6 – Bài tập kèm đáp án PDF
Phép cộng trừ các số nguyên lớp 6 – Bài tập kèm đáp án PDF dưới đây sẽ tổng hợp đầy đủ các dạng toán cộng trừ số nguyên lớp 6, kèm theo ví dụ minh họa và bài tập tự luyện có đáp án chi tiết. Đặc biệt, bạn có thể tải về file PDF để ôn luyện mọi lúc mọi nơi.
Mời quý phụ huynh, thầy cô và các em tham khảo!
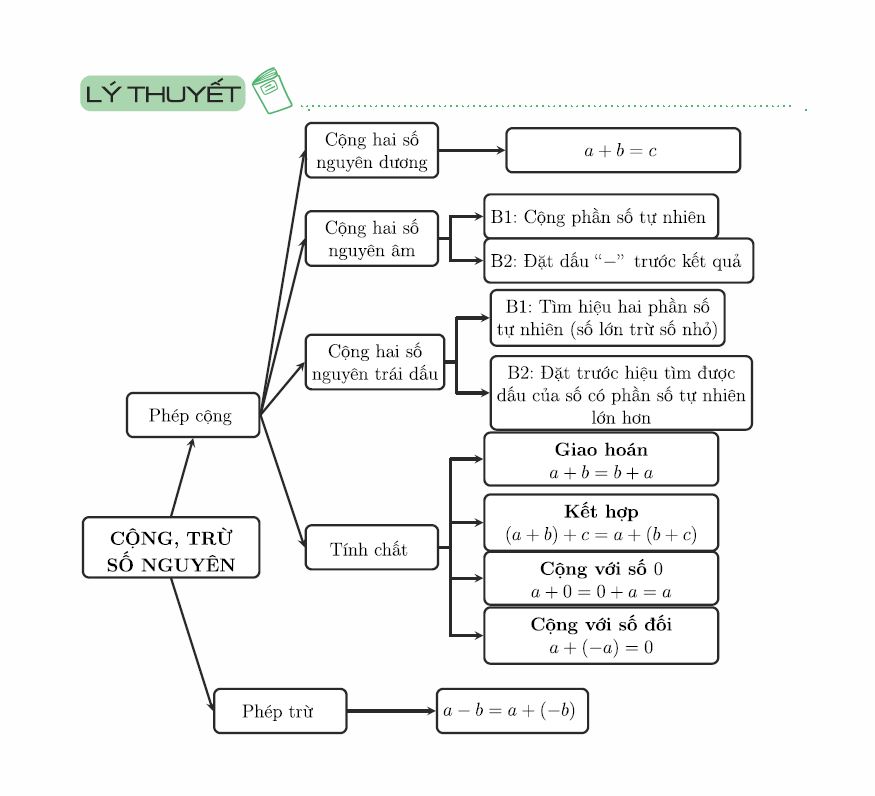
A. Các dạng toán về phép cộng trừ số nguyên lớp 6
Dạng 1: Thực hiện phép tính cộng các số nguyên
♦ Phương pháp
- Vận dụng quy tắc cộng, trừ hai số nguyên.
- Thứ tự thực hiện phép tính.
- Tính chất của phép cộng số nguyên.
♦ Các ví dụ
Ví dụ 1
Thực hiện phép tính:
a) 73 + 47
b) (−13) + (−29)
c) (−132) + (−255)
d) (−175) + 175
e) (−45) + 33
f) (−14) + 24.
Hướng dẫn giải
a) 73 + 47 = 120
b) (−13) + (−29) = −42
c) (−132) + (−255) = −387
d) (−175) + 175 = 0
e) (−45) + 33 = −12
f) (−14) + 24 = 10
Ví dụ 2
Tính:
a) 13 − 15
b) 5 − (−4)
c) 0 − (−9)
d) (−6) − (−2)
Hướng dẫn giải
a) 13 − 15 = 13 + (− 15) = − (15 − 13) = −2.
b) 5 − (−4) = 5 + 4 = 9.
c) 0 − (−9) = 0 + 9 = 9.
d) (−6) − (−2) = − 6 + 2 = − (6 − 2) = − 4.
Ví dụ 3
Tính giá trị của biểu thức:
a) x + (−125) với x = −35
b) (−234) + y với y = 73
c) (−115) + y + (−x) với x = 23, y = 75
d) x + (−132) + y với x = −65, y = 43
Hướng dẫn giải
a) (−35) + (−125) = −160.
b) (−234) + 73 = −161.
c) (−115) + 75 + (−23) = −63.
d) (−65) + (−132) + 43 = −154.
Dạng 2: Tính hợp lí
♦ Phương pháp
Sử dụng tính chất của phép cộng số nguyên, nhóm các số có tổng là các số tròn chục để tính hợp lí.
♦ Các ví dụ
Ví dụ 4
Tính một cách hợp lí:
a) (−37) + 14 + 26 + 37
b) 60 + 33 + (−50) + (−33)
c) (−16) + (−209) + (−14) + 209s
Hướng dẫn giải
a) (−37) + 14 + 26 + 37 = [(−37) + 37] + (14 + 26) = 0 + 40 = 40.
b) 60 + 33 + (−50) + (−33) = [(−33) + 33] + [60 + (−50)] = 0 + 10 = 10.
c) (−16) + (−209) + (−14) + 209 = [(−16) + (−14)] + [209 + (−209)] = −30 + 0 = −30.
Ví dụ 5
Tính tổng các số nguyên x, biết:
a) −25 ≤ x ≤ 25
b) −42 < x < 45
c) −34 < x ≤ 32
d) −5 ≤ x ≤ 13.
Hướng dẫn giải
a) Từ −25 ≤ x ≤ 25 ⇒ x ∈ {−25; −24; −23; …; 24; 25}. Tổng các số x là
(−25) + (−24) + (−23) + … + 24 + 25 =
= [(−25) + 25] + [(−24) + 24] + … [(−1) + 1] + 0 = 0.
b) Từ −42 < x < 45 ⇒ x ∈ {−41; −40; −39; …; 43; 44}. Tổng các số x là
(−41) + (−40) + (−39) + … + 3 + 4 =
= [(−41) + 41] + [(−40) + 40] + … [(−1) + 1] + 0 + 42 + 43 + 44 = 129.
c) Từ −34 < x ≤ 32 ⇒ x ∈ {−33; −32; −31; …; 31; 32}. Tổng các số x là
(−33) + (−32) + (−31) + … + 31 + 32 =
= [(−32) + 32] + [(−31) + 31] + … [(−1) + 1] + 0 + (−33) = −33.
d) Từ −5 ≤ x ≤ 13 ⇒ x ∈ {−5; −4; −3; …; 12; 13}. Tổng các số x là:
(−5) + (−4) + (−3) + … + 12 + 13 =
= [(−5) + 5] + [(−4) + 4] + … [(−1) + 1] + 0 +
(6 + 13) + (7 + 12) + (8 + 11) + (9 + 10) = 0 + 0 + 0 + … + 0 + 19 + 19 + 19 + 19 = 76.
Dạng 3: Toán có nội dung lời văn
Ví dụ 6
Hai đoàn tàu hỏa xuất phát cùng một lúc từ Huế đi về hai phía Hà Nội và thành phố Hồ Chí Minh. Ta quy ước chiều từ Huế đến Hà Nội là chiều dương, chiều ngược lại từ Huế đến thành phố Hồ Chí Minh là chiều âm.
Hỏi sau 1 giờ hai đoàn tàu cách nhau bao nhiêu ki lô mét nếu vận tốc của chúng lần lượt là:
a) 45 km/h và 40 km/h.
b) 45 km/h và −40 km/h.
Hướng dẫn giải
a) Vận tốc của hai tàu hỏa là 45 km/h và 40 km/h, nghĩa là cả hai đoàn tàu cùng đi từ Huế ra Hà Nội (cùng chiều). Do đó sau một giờ chúng cách nhau là:
45 − 40 = 5 (km/h).
b) Vận tốc của hai tàu hỏa là 45 km/h và −40 km/h, nghĩa là một đoàn tàu đi từ Huế ra Hà Nội còn đoàn tàu kia đi từ Huế vào thành phố Hồ Chí Minh (ngược chiều). Do đó sau một giờ chúng cách nhau là:
45 + 40 = 85 (km/h).
Ví dụ 7
Trong lễ hội thả diều ở Festival diều Huế, chiếc diều của Việt Nam mang biểu tượng hình chữ S bay ở đội cao 150 m (so với mặt đất). Sau một lúc chiếc diều giảm độ cao 15 m, rồi sau đó lại tăng thêm 30 m. Hỏi sau hai lần thay đổi diều ở độ cao bao nhiêu mét (so với mặt đất)?
Hướng dẫn giải
Diều giảm độ cao 15 m và sau đó tăng thêm 30 m có nghĩa là tăng thêm −15 m.
Nên độ cao của diều sau hai lần thay đổi là:
150 + (−15) + 30 = 165 (m).
Vậy sau hai lần thay đổi độ cao thì độ cao của nó là 165 m.
Dạng 4: Toán tổng hợp
Ví dụ 8
Cho a, b là các số nguyên. Chứng minh:
a) Nếu b > 0 thì a + b > a.
b) Nếu b < 0 thì a + b < a.
Hướng dẫn giải
a) Vì b > 0 nên a + b > a + 0 vậy a + b > a.
b) Vì b < 0 nên a + b < a + 0 vậy a + b < a.
Ví dụ 9
Chứng minh với mọi số tự nhiên a có một số nguyên b sao cho a + b = 0.
Hướng dẫn giải
Thật vậy, chẳng hạn a ∈ N thì có b = −a sao cho a + b = a + (−a) = 0.
Vậy hiển nhiên b ∈ N.
>>> Tải file phép cộng trừ các số nguyên lớp 6 – Bài tập kèm đáp án dưới dạng PDF miễn phí tại đây!
B. Bài tập cộng trừ số nguyên lớp 6
Bài tập trắc nghiệm
14.1. Tổng của hai số nguyên (–3) và (–5) là:
A. 8.
B. (–8).
C. (–2).
D. 2.
Đáp án
Phép tính:
(–3) + (–5) = –(3 + 5) = –8
✅ Đáp án đúng: B. (–8)
14.2. Hai số nguyên đối nhau có tổng là:
A. 1.
B. là số dương.
C. là số nguyên âm.
D. 0.
Đáp án
Quy tắc: Hai số nguyên đối nhau (ví dụ: a và –a) khi cộng lại luôn bằng 0.
Ví dụ: 5 + (–5) = 0
✅ Đáp án đúng: D. 0
14.3. Kết quả phép tính –20 –15 là:
A. –35.
B. –5.
C. 35.
D. 5.
Đáp án
Đây là phép trừ hai số nguyên.
–20 – 15 = –20 + (–15) = –35
✅ Đáp án đúng: A. –35
14.4. Kết quả của phép tính 35 + (–47) bằng:
A. 82.
B. –12.
C. –82.
D. 12.
Đáp án
35 + (–47) = –(47 – 35) = –12
✅ Đáp án đúng: B. –12
14.5. Kết quả của phép tính –23 – (–17) là:
A. –40.
B. –6.
C. 40.
D. 6.
Đáp án
–23 – (–17) = –23 + 17 = –6
✅ Đáp án đúng: B. –6
14.6. Tổng của các số nguyên x, y, z . Biết x = − 17, y = 25, z = 17 bằng:
A. 9.
B. -9.
C. 25.
D. 59.
Đáp án
Tổng = –17 + 25 + 17 = (–17 + 17) + 25 = 0 + 25 = 25
✅ Đáp án đúng: C. 25
14.7. Giá trị của biểu thức x + y − z với x = − 2840; y = 840; z = 11.
A. 2011.
B. 3691.
C. –2011.
D. –3691.
Đáp án
Tính:
–2840 + 840 – 11 = (–2000) – 11 = –2011
✅ Đáp án đúng: C. –2011
14.8. Cho A = x + 12 + (−34) + (−32) + 20 + (−26), biết biểu thức A có giá trị là số nguyên âm nhỏ nhất có hai chữ số. Số x có giá trị bằng:
A. 50.
B. 39.
C. –50.
D. –39.
Đáp án
Số nguyên âm nhỏ nhất có hai chữ số là –10.
=> biểu thức là: –10 = x + 12 + (−34) + (−32) + 20 + (−26)
–10 = x + (–60)
x = –10 + 60 = 50.
✅ Đáp án đúng: A. 50
14.9. Biết 4 = 1 + (−2) + 3 + (-4) + 5 + (-6) + … + 39 + (− 40). Giá trị của biểu thức A bằng:
A. 20.
B. –20.
C. –40.
D. 40
Đáp án
Ta nhóm từng cặp:
(1 + –2) = –1
(3 + –4) = –1
…
(39 + –40) = –1
Tổng số cặp là: từ 1 đến 40 → có 20 cặp
→ Tổng = 20 × (–1) = –20
✅ Đáp án đúng: B. –20
14.10. Thay * bằng chữ số thích hợp 38 + (−2*) = 15.
A. -3.
B. 3.
C. 7.
D. -7.
Đáp án
38 + (−2*) = 15 → (−2*) = 15 – 38 = −23
Vậy chữ số trong dấu * là 3.
✅ Đáp án đúng: B. 3.
Bài tập tự luận
14.11. Tính
a) 2763 + 152
b) (−35) + (−9)
c) (−23) + 105
d) (−7) + (−14)
e) (−5) + (−248)
f) 78 + (−123)
g) (−2) + 7 + (−12) + 17 + (−22) + 27
h) 1 + (−6) + 11 + (−16) + 21 + (−26)
Đáp án
a) 2763 + 152 = 2915
b) (−35) + (−9) = −(35 + 9) = −44
c) (−23) + 105 = 105 − 23 = 82
d) (−7) + (−14) = −(7 + 14) = −21
e) (−5) + (−248) = −(5 + 248) = −253
f) 78 + (−123) = 78 − 123 = −45
g) (−2) + 7 + (−12) + 17 + (−22) + 27
→ Tính theo nhóm:
(−2 + 7) = 5
(−12 + 17) = 5
(−22 + 27) = 5
Tổng = 5 + 5 + 5 = 15
h) 1 + (−6) + 11 + (−16) + 21 + (−26)
→ (1 + (−6)) = −5
(11 + (−16)) = −5
(21 + (−26)) = −5
Tổng = −5 × 3 = −15
14.12. Tính
a) 231 − 452
b) (−415) − 137
c) 288 − (−112)
d) (−734) − (−366)
Đáp án
a) 231 − 452 = −221
b) (−415) − 137 = −415 + (−137) = −552
c) 288 − (−112) = 288 + 112 = 400
d) (−734) − (−366) = −734 + 366 = −368
14.13. Tính hiệu của số nguyên âm nhỏ nhất có hai chữ số và số nguyên âm lớn nhất.
Đáp án
Số nguyên âm nhỏ nhất có hai chữ số: −99
Số nguyên âm lớn nhất: −1
Hiệu: (−99) − (−1) = −99 + 1 = −98
14.14. Tính
a) 367 + (−30) + 1672 + (−337)
b) (−299) + (−300) + (−201)
Đáp án
a) 367 + (−30) + 1672 + (−337)
= (367 − 30) + (1672 − 337) = 337 + 1335 = 1672
b) (−299) + (−300) + (−201)
= −(299 + 300 + 201) = −800
→ Đáp án: −800
14.15. Tính tổng các số nguyên x, biết:
a) x là số nguyên âm lớn hơn −5 → {−4, −3, −2, −1}
b) −13 ≤ x < 15.
Đáp án
a) x là số nguyên âm lớn hơn −5
→ x ∈ {−4, −3, −2, −1}
Tổng = (−4) + (−3) + (−2) + (−1) = −10
b) −13 ≤ x < 15
→ x ∈ {−13, −12, …, 14}
Đây là dãy số nguyên liên tiếp từ −13 đến 14.
Tổng = [(số đầu + số cuối) × số phần tử] ÷ 2
Số phần tử = 14 − (−13) + 1 = 28
Tổng = (−13 + 14) × 28 ÷ 2 = 1 × 14 = 14
14.16. Tính giá trị biểu thức.
a) (–20) − x với x = 36
b) a − b với a = 24, b = −54.
Đáp án
a) (−20) − x với x = 36
→ −20 − 36 = −56
b) a − b với a = 24, b = −54
→ 24 − (−54) = 24 + 54 = 78
14.17. Tính tổng S = 1 + (−2) + 3 + (−4) + … + 99 + (−100).
Đáp án
Chuỗi xen kẽ: số lẻ dương + số chẵn âm
→ Cặp: (1 + (−2)), (3 + (−4)), …, (99 + (−100))
→ Có 50 cặp như vậy: mỗi cặp = −1
Vậy tổng S = −1 x 50 = −50.
14.18. Tìm số nguyên x, biết:
Tìm x, biết
a) 17 − (12 + x) = 23
b) (−9) − (25 − x) = 32
c) (28 + x) − (47 − 115) = −236.
Đáp án
a) 17 − (12 + x) = 23
→ 17 − 12 − x = 23
→ 5 − x = 23
→ x = 5 − 23 = −18
b) (−9) − (25 − x) = 32
→ −9 − 25 + x = 32
→ x − 34 = 32
→ x = 66
c) (28 + x) − (47 − 115) = −236
→ (28 + x) − (−68) = −236
→ 28 + x + 68 = −236
→ x + 96 = −236
→ x = −236 − 96 = −332
14.19. Cho 10 ô liên tiếp
| -5 | -9 |
Hãy điền các số vào ô trống sao cho tổng ba số ở ba ô liền nhau bằng 0.
Đáp án
Dãy số hoàn thiện là:
| – 9 | -5 | 14 | – 9 | – 5 | 14 | -9 | – 5 | 14 | – 9 |
14.20. Tìm các số nguyên x, y, z, biết x + y = 11; y + z = 3; z + x = 2.
Đáp án
Cộng (1) và (2):
x + y + y + z = 11 + 3 → x + 2y + z = 14 (4)
Từ (3): z + x = 2
→ Thay vào (4): (z + x) + 2y = 2 + 2y = 14
→ 2 + 2y = 14 ⇒ 2y = 12 ⇒ y = 6
Thay y = 6 vào (1): x + 6 = 11 ⇒ x = 5
Thay y = 6 vào (2): 6 + z = 3 ⇒ z = −3
✅ Đáp án: x = 5, y = 6, z = −3
Những bài tập cộng trừ số nguyên lớp 6 kèm đáp án PDF bạn vừa xem được trích từ cuốn “Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 6 – Tập 1” – một tài liệu học tập được thiết kế sinh động, hệ thống kiến thức bằng sơ đồ tư duy trực quan, giúp học sinh tiếp thu nhanh, ghi nhớ sâu và vận dụng linh hoạt trong mọi dạng bài.
📥 Đọc thử và đặt mua cuốn sách này ngay hôm nay để học tập hiệu quả và tiết kiệm thời gian ôn luyện các em nhé!
Link đọc thử và đặt mua sách để nhận ưu đãi: https://lamchu.tkbooks.vn/lop6



Pingback: Bài tập số nguyên lớp 6 PDF – Bộ đề ôn tập chất lượng cao