Nguyên hàm là gì và ứng dụng của nguyên hàm trong thực tế

Nguyên hàm và ứng dụng của nguyên hàm là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.

Dưới đây là toàn bộ kiến thức về Nguyên hàm và ứng dụng của nguyên hàm. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!

I. NGUYÊN HÀM LÀ GÌ VÀ TÍNH CHẤT CỦA NGUYÊN HÀM

1. Nguyên hàm là gì

Hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của f(x) trên K nếu:

F(x) = f(x) + C, ∀x ∈ K.

Hàm số F(x) xác định trên K . Hàm số f(x) được gọi là họ nguyên hàm của F(x) trên K nếu:

∫f(x)dx = F(x) + C, const = C ∈ R

Nếu mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

Ví dụ:

• Hàm số f(x) = 2x có nguyên hàm là F(x) = (x² + C) vì  (x² + C)’ = 2x.
• Hàm số f(x) = sinx có nguyên hàm là F(x) = -cosx + C vì (−cosx + C)’ =sinx.

2. Tính chất của nguyên hàm

[∫f(x)dx]’ = ∫f’(x)dx = f(x) + C ∫k.f(x)dx = k.∫f(x)dx với k ≠0 ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx + C ∫f(x)dx = F(x) + C ⇒ ∫f(u(x)).u’(x)dx = F(u(x)) + C

II. BẢNG NGUYÊN HÀM CÁC HÀM SỐ CƠ BẢN

III. MỘT SỐ PHƯƠNG PHÁP TÌM NGUYÊN HÀM

1. Phương pháp đổi biến số

Giả sử ta cần tìm họ nguyên hàm I = ∫f(x)dx, trong đó ta có thể phân tích f(x) = g[u(x)].u'(x) thì ta thực hiện phép đổi biến số t = u(x), suy ra dt =u'(x).dx .

Khi đó ta được nguyên hàm:

∫[g(t)dt = G(t) + C = G[u(t)] + C.

Chú ý. Sau khi tìm được họ nguyên hàm theo t thì ta phải thay t = u(x).

2. Phương pháp tính nguyên hàm của hàm số hữu tỷ I = ∫[P(x)/Q(x)]dx

• Nếu bậc của tử số P(x) ≥ bậc của mẫu số Q(x) thì ta sử dụng phương pháp Chia đa thức.
• Nếu bậc của tử số P(x) ≤ bậc của mẫu số Q(x) thì ta phân tích mẫu Q(x) thành tích số, rồi sử dụng phương pháp chia để đưa về công thức nguyên hàm số.
• Nếu mẫu không phân tích được thành tích số thì ta thêm bớt để đổi biến hoặc lượng giác hóa bằng cách đặt X = a.tan t, nếu mẫu đưa được về dạng X² + a².

3. Phương pháp lấy nguyên hàm từng phần

Cho hai hàm số u và v liên tục trên đoạn [a;b] và có đạo hàm liên tục trên đoạn [a;b].

Khi đó:

∫udv = uv – ∫vdu (*).

Để tính nguyên hàm ∫f(x)dx bằng từng phần ta làm như sau:

• B1: Chọn u, v sao cho f(x)dx = udv (chú ý dv = v'(x).dx).

Sau đó tính: v = ∫dv và du = u’.dx

Chú ý: Đặt u theo thứ tự ưu tiên: “Nhất LOG – Nhì ĐA – Tam LƯỢNG – Tứ MŨ”

• B2: Thay vào công thức (*) và tính ∫vdu

Chú ý: Cần phải lựa chọn u và dv hợp lí sao cho ta dễ dàng tìm được v và tích phân ∫udv dễ tính hơn ∫udv.

Ta thường gặp các dạng sau:

IV. ỨNG DỤNG THỰC TIỄN CỦA NGUYÊN HÀM

Giả sử v(t), a(t) là vận tốc, gia tốc của vật M tại thời điểm t và s(t) là quãng đường vật đi được sau khoảng thời gian t tính từ lúc bắt đầu chuyển động. Ta có các mối liên hệ giữa s(t), v(t) và a(t) như sau:

• s'(t) = v(t);
• v'(t) = a(t).

Nguyên hàm của gia tốc là vận tốc: v(t) = ∫a(t)dt .

Nguyên hàm của vận tốc là quãng đường s(t) = ∫v(t)dt .

Từ đây ta cũng có quãng đường vật đi được trong khoảng thời gian t = [a; b] là:

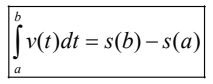
V. Bài tập

Dưới đây là một số dạng toán cơ bản về Nguyên hàm và ứng dụng của nguyên hàm để các em luyện tập:

Các dạng toán khác về Nguyên hàm và ứng dụng của nguyên hàm được ghi chú và diễn giải rất đầy đủ trong cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!

Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.

Tkbooks.vn