Hệ thức Vi ét và ứng dụng – Lý thuyết và 7 dạng bài tập liên quan
Hệ thức Vi ét và ứng dụng là một công cụ không thể thiếu giúp giải quyết nhiều bài toán đại số phức tạp một cách hiệu quả.
Qua bài viết “Hệ thức Vi ét và ứng dụng – Lý thuyết và 7 dạng bài tập liên quan” dưới đây, Tkbooks sẽ mang đến cho các em một nguồn tài liệu tham khảo giá trị, giúp các em hiểu sâu sắc hơn về cách thức và phương pháp áp dụng hệ thức Vi ét vào giải các dạng bài tập.
Bài viết không chỉ đi sâu vào lý thuyết mà còn hướng dẫn chi tiết cách giải 7 dạng bài tập thường gặp, từ đơn giản đến nâng cao, qua đó giúp bạn củng cố và nâng cao kỹ năng giải toán.
Hãy cùng khám phá và làm chủ những bài toán này để tự tin hơn trong học tập và chuẩn bị tốt cho những kỳ thi sắp tới.
I. Lý thuyết về hệ thức Vi ét và ứng dụng
- Nếu x1, x2 là hai nghiệm của phương trình ax2 + bx + c = 0 (a ≠ 0) thì:
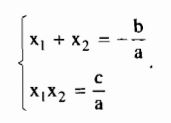
- Muốn tìm hai số u và v, biết u + v = S, uv = P, ta giải phương trình x2 – Sx + P = 0. (Điều kiện để có u và v là S2 – 4P ≥ 0).
- Nếu a + b + c = 0 thì phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1 = 1, x2 = c/a.
- Nếu a – b + c = 0 thì phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1 = – 1, x2 = -c/a.
II. Các dạng toán về hệ thức Vi ét và ứng dụng
Dạng 1: Giải phương trình bậc hai bằng cách nhẩm nghiệm
+ Phương pháp
Phương trình bậc hai ax2 + bx + c = 0 (a≠0):
- Nếu a + b + c = 0 thì phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1 = 1, x2 = c/a.
- Nếu a – b + c = 0 thì phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1 = – 1, x2 = – c/a.
Nếu x1, x2 là hai nghiệm của phương trình thì:
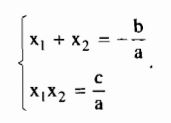
Nhận xét: Để tính tổng và tích hai nghiệm của phương trình theo hệ thức Vi-ét, ta cần tìm điều kiện để phương trình bậc hai có nghiệm.
+ Các ví dụ
Ví dụ 1: Nhẩm nghiệm của các phương trình sau:
a) -3x2 + 8x – 5 = 0;
b) x2 + (1 – √5)x – √5 = 0.
Lời giải:
a) Vì −3 + 8 + (−5) = 0 nên phương trình có hai nghiệm x1 = 1; x2 = 5/3.
b) Vì 1 – (1 – √5 ) – √5 = 0 nên phương trình có hai nghiệm x = −1; x2 = √5.
Ví dụ 2: Cho phương trình (2m + 1)x2 – (m + 4)x + 3 – m = 0 với m là tham số. Chứng minh phương trình luôn có một nghiệm không phụ thuộc vào tham số m.
Lời giải:
Với m = -1/2 phương trình có dạng:
(-7/2)x + 7/2 = 0 ⇒ x = 1.
Với m ≠ -1/2. Ta có: 2m + 1 − (m + 4) + 3 – m = 0 => phương trình có hai nghiệm:
x1 = 1; x2 = (3 – m)/(2m + 1).
Vậy phương trình luôn có nghiệm x = 1 với mọi giá trị của m.
Dạng 2: Tìm hai số khi biết tổng và tích
+ Phương pháp
Nếu hai số u, v có tổng S = u + v và tích P = uv thì u, v là hai nghiệm của phương trình x2 + Sx + P = 0 (điều kiện có nghiệm là S2 − 4P > 0).
+ Các ví dụ
Ví dụ 3: Tìm hai số u, v biết:
a) u + v = 12 và uv = 32;
b) u + v = – 8 và uv = – 33;
Lời giải:
a) Hai số u,v là hai nghiệm của phương trình x2 − 12x + 32 = 0. Ta có: Δ’ = 4 => phương trình có hai nghiệm phân biệt là x1 = 8; x2 = 4.
Vậy (u;v) € {(8;4);(4;8)}.
b) (u; v) = {(3;-11); (−11;3)}.
Ví dụ 4: Lập phương trình bậc hai có hai nghiệm là:
a) 1 – 2√3 và 1 + 2√3;
b) (1 + √3)/2 và (1 – √3)/2.
Lời giải:
a) Ta có:
S = 1 – 2√3 + 1 + 2√3 = 2
P = (1 – 2√3)(1 + 2√3) = – 11.
→ phương trình bậc hai là: x2 − 2x – 11 = 0.
b) Ta có:
S = (1 + √3)/2 + (1 – √3)/2 = 1
P = [(1 + √3)/2].[(1 – √3)/2] = – 1/2
→ phương trình bậc hai là: x2 – x – ½ = 0.
Dạng 3: Lập phương trình bậc hai biết điều kiện của hai nghiệm
+ Phương pháp
Nếu S = x1 + x2 và P = x1x2 thì x1, x2 là hai nghiệm của phương trình X2 – SX + P = 0.
+ Các ví dụ
Ví dụ 5: Cho phương trình x2 + 5x – 1 = 0. Gọi x1, x2 là hai nghiệm của phương trình.
Không giải phương trình, hãy lập phương trình bậc hai có hai nghiệm là 1/x1 và 1/x2.
Lời giải:
Phương trình x2 + 5x – 1 = 0 có ac = -1 < 0 => phương trình có hai nghiệm phân biệt x1,x2.
Theo hệ thức Vi-ét, ta có:
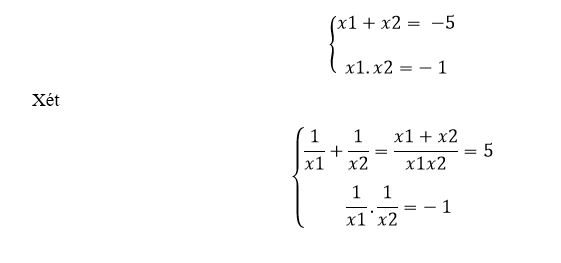
Ví dụ 6: Lập phương trình bậc hai có hai nghiệm 1/x1 và 1/x2, biết x1, x2 là hai nghiệm của phương trình x2 – 2mx + m2 – 1 = 0.
Lời giải:
Có x1, x2 là hai nghiệm của phương trình x2 – 2mx + m2 – 1 = 0, theo hệ thức Vi-ét, ta có:
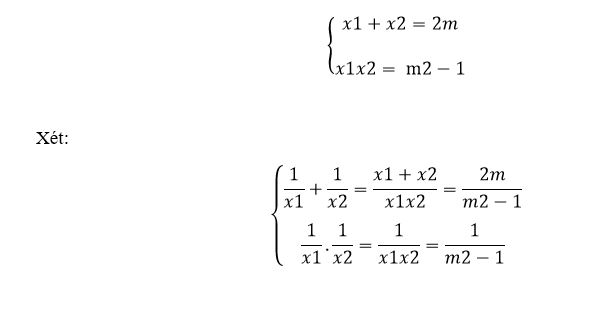
⇒ phương trình bậc hai có hai nghiệm 1/x1 và 1/x2 là X2 – [2m/(m2 – 1)]X + 1/(m2 – 1) = 0.
Dạng 4: Tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào tham số
+ Phương pháp
Phương trình bậc hai ax + bx + c = 0 (a ≠ 0):
- Bước 1: Xét điều kiện để phương trình có nghiệm: Δ ≥ 0.
- Bước 2: Sử dụng hệ thức Vi-ét để tính tổng và tích của hai nghiệm.
- Bước 3: Khử tham số.
+ Các ví dụ
Ví dụ 7: Cho phương trình x2 + 2mx – m – 2 = 0 có hai nghiệm x1, x2. Tìm hệ thức liên hệ giữa x1, x2 không phụ thuộc vào tham số m.
Lời giải:
Ta có: Δ’ = m2 + m + 2 = (m + ½)2 + 7/4 > 0 với mọi m => phương trình luôn có hai nghiệm phân biệt x1, x2.
Theo hệ thức Vi-ét:
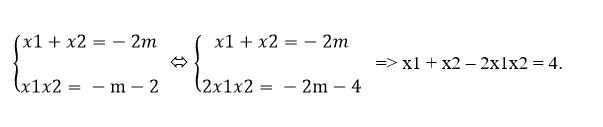
Ví dụ 8: Cho phương trình (m + 1)x2 – 2mx + m – 1 = 0 với m là tham số.
a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với m khác −1.
b) Tìm hệ thức liên hệ giữa hai nghiệm phân biệt x, X, của phương trình không phụ thuộc vào tham số m.
Lời giải:
a) Với m ≠ -1 => m + 1 ≠ 0, ta có: Δ’ = m2 – (m + 1)(m − 1) = 1 > 0.
=> phương trình luôn có hai nghiệm phân biệt với m ≠ -1.
b) Theo hệ thức Vi-ét, ta có:
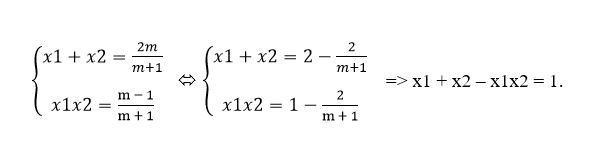
Dạng 5: Tính giá trị biểu thức đối xứng giữa các nghiệm của phương trình bậc hai
+ Phương pháp
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0):
- Bước 1: Tìm điều kiện để phương trình có nghiệm
- Bước 2: Áp dụng hệ thức Vi-ét, ta có:
- Bước 3: Biến đổi biểu thức đối xứng giữa các nghiệm theo tổng x1 + x2 và tích x1x2. Sau đó áp dụng bước 2.
Một số biểu thức đối xứng giữa x1, x2 thường gặp là:
A = x12 + x22 = (x1 + x2)2 − 2x1x2;
B = x13 + x23 = (x1 + x2)3 − 3x1x2 (x1 + x2);
C = x14 + x24 = (x12 + x22)2 − 2×12x22 = [(x1 + x2)2 − 2x1x2]2 − 2×12x22;
D = |x1 − x2| = √(x1 − x2)2 = √[(x1 + x2)2 − 4x1x2] ⋅
+ Các ví dụ
Ví dụ 9: Gọi x1, x2 là hai nghiệm của phương trình x2 − 5x – 8 = 0. Không giải phương trình, hãy tính giá trị của các biểu thức sau:
a) A = x12 + x2;
b) B = 1/x1 |+ 1/x2
c) C = 1/x12 + 1/x22
d) D = x13 + x23
Lời giải:
Ta có: Δ = 57 > 0 nên phương trình có hai nghiệm phân biệt x1, x2.
Theo hệ thức Vi-ét, ta có:
a) A = (x1 + x2)2 – 2x1x2 = 41.
b) B = (x1 + x2)/x1x2 = – 5/8
c) C = [(x1 + x2)2 – 2x1x2]/x12x22 = 41/64
d) D = (x1 + x2)3 – 3x1x2(x1 + x2) = 245.
Ví dụ 10: Gọi x1, x2 là hai nghiệm của phương trình –x2 + 7x – 1 = 0. Không giải phương trình, hãy tính giá trị của các biểu thức sau:
a) A = x1 + 1/x1 + x2 + 1/x2
b) 1/(2×1 – 7) + 1/(2×2 – 7)
Lời giải:
Ta có: Δ = 45 > 0 => phương trình có hai nghiệm phân biệt x1, x2.
Theo hệ thức Vi-ét, ta có:
a) A= (x1 + x2) + (x1 + x2)/x1x2 = 14.S
b) B = [2(x1 + x2) -14]/[4x1x2 -14(x1 + x2) + 49] = 0.
Dạng 6: Xét dấu các nghiệm của phương trình bậc hai
+ Phương pháp
Xét phương trình ax2 + bx + c = 0 (a ≠ 0). Khi đó:

+ Các ví dụ
Ví dụ 11: Cho phương trình x2 – 2(m−3)x + 4m – 1 = 0. Xác định m để phương trình có hai nghiệm trái dấu.
Lời giải:
Phương trình có hai nghiệm trái dấu ↔ ac = 4m – 1 < 0 ↔ m < ¼.
Ví dụ 12: Cho phương trình x2 – 2(m + 1) + m – 4 = 0. Xác định m để phương trình có hai nghiệm cùng dương.
Lời giải:
Ta có: Δ’ = m2 + m + 5 = (m -1/2)2 + 19/4 > 0 với mọi m.
⇒ phương trình luôn có hai nghiệm phân biệt.
Để phương trình có hai nghiệm cùng dương thì:
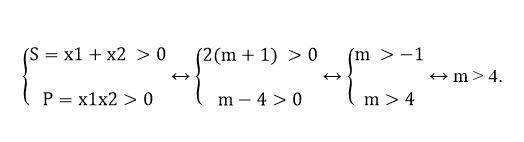
Dạng 7: Giải hệ phương trình đối xứng hai ẩn
+ Phương pháp
Hệ phương trình đối xứng hai ẩn là hệ phương trình có hai ẩn x và y mà nếu đổi x và y cho nhau thì hệ không thay đổi.
- Bước 1: Đặt ẩn phụ
- Biến đổi đưa về hệ hai ẩn S, P.
- Bước 2: Giải hệ để tìm S, P.
Bước 3: Do đó, x, y là nghiệm của phương trình X2 – SX + P = 0 (điều kiện để phương trình có nghiệm là S2 ≥ 4P).
+ Các ví dụ

Hy vọng rằng, bài viết “Hệ thức Vi ét và ứng dụng – Lý thuyết và 7 dạng bài tập liên quan” ở trên đã cung cấp cho các em những kiến thức bổ ích và các phương pháp giải toán hiệu quả.
Để tìm hiểu thêm về kiến thức Toán lớp 9 trong học kỳ 2, các em nên mua cuốn sách Làm chủ kiến thức Toán 9 ôn thi vào 10 phần Đại số của Tkbooks nhé!
Link đọc thử sách:https://drive.google.com/file/d/1uaOJCek1Mpmm-UbFU3hEIVzQ0P6PPaoC/view
TKbooks tự hào là nhà xuất bản sách tham khảo cho học sinh THCS hàng đầu tại Việt Nam.

