Chưa có sản phẩm trong giỏ hàng.
Hệ thức lượng trong tam giác vuông lớp 9 đầy đủ nhất
Hệ thức lượng trong tam giác vuông là một trong những kiến thức cốt lõi và quan trọng của chương trình Toán lớp 9. Được xem là nền tảng để học sinh hiểu sâu hơn về hình học và đại số, các hệ thức này không chỉ giúp giải quyết các bài toán về tam giác vuông mà còn mở ra nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày.
Bài viết dưới đây của TKbooks sẽ giúp các em học sinh lớp 9 nắm vững các công thức, định lý quan trọng và cách áp dụng chúng vào các bài toán cụ thể. Hãy cùng TKBooks khám phá và làm chủ hệ thức lượng trong tam giác vuông, từ đó nâng cao kết quả học tập và chuẩn bị tốt nhất cho các kỳ thi sắp tới.
Mời các em tham khảo!
I. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
1. Lý thuyết về cạnh và đường cao trong tam giác vuông

2. Bài tập vận dụng về cạnh và đường cao trong tam giác vuông
Bài 1. Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
Bài 2. Cho tam giác ABC vuông tại A có AC = 10cm, AB = 8cm. AH là đường cao. Tính BC, BH, CH, AH.
Bài 3. Cho tam giác ABC vuông tại A có BC = 12cm. Tính chiều dài hai cạnh góc vuông biết AB = 2/3 AC .
Bài 4. Cho tam giác ABC vuông tại A có đường cao AH. Biết BH = 10cm, CH = 42 cm. Tính BC, AH, AB và AC.
Bài 5. Hình thang cân ABCD có đáy lớn AB = 30cm, đáy nhỏ CD = 10cm và góc A là 60°.
a) Tính cạnh BC.
b) Gọi M, N lần lượt là trung điểm AB và CD. Tính MN.
Bài 6. Cho tứ giác lồi ABCD có AB = AC = AD = 10cm, góc B bằng 60° và góc A là 90°.
a) Tính đường chéo BD.
b) Tính các khoảng cách BH và DK từ B và D đến AC.
c) Tính HK.
d) Vẽ BE ⊥ DC kéo dài. Tính BE, CE và DC.
Bài 7. Cho đoạn thẳng AB = 2a. Từ trung điểm O của AB vẽ tia Ox ⊥ AB. Trên Ox, lấy điểm D sao cho OD = a/2. Từ B kẻ BC vuông góc với đường thẳng AD.
a) Tính AD, AC và BC theo a.
b) Kéo dài DO một đoạn OE = a. Chứng minh bốn điểm A, B, C và E cùng nằm trên một đường tròn.
Bài 8. Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H. Trên HB và HC lần lượt lấy các điểm M, N sao cho góc AMC = góc ANB = 90°. Chứng minh: AM = AN.
Bài 9. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB/AC = 20/21 và AH = 420. Tính chu vi tam giác ABC.
Bài 10. Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB = 2√13, OA = 6, tính diện tích hình thang ABCD.
II. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
1. Lý thuyết về tỉ số lượng giác của góc nhọn

2. Bài tập vận dụng về tỉ số lượng giác của góc nhọn
Bài 11. Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 64cm và CH = 81cm. Tính các cạnh và góc tam giác ABC.
Bài 12. Cho tam giác ABC vuông tại A. Tìm các tỉ số lượng giác của góc B khi:
a) BC = 5cm, AB = 3cm.
b) BC = 13 cm, AC = 12 cm.
c) AC = 4cm, AB = 3cm.
Bài 13. Cho tam giác ABC vuông tại A, có AB = 10cm và AC = 15cm.
a) Tính góc B.
b) Phân giác trong góc B cắt AC tại I. Tính AI.
c) Vẽ AH ⊥ BI tại H. Tính AH.
Bài 14. Tính giá trị các biểu thức sau:
a) cos2 15° + cos2 25° + cos2 35° + cos2 45° + cos2 55° + cos2 65° + cos2 75°.
b) sin2 10°- sin2 20° + sin2 30°- sin2 40°- sin2 50° – sin2 70° + sin2 80°.
c) sin 15° + sin 75° – cos 15° – cos 75° + sin 30°
d) sin 35° + sin 67° – cos 23° – cos 55°
e) cos2 20° + cos2 40° + cos2 50° + cos2 70°
f) sin 20°- tan 40° + cot 50° – cos 70°
Bài 15. Cho biết một tỉ số lượng giác của góc nhọn a, tính các tỉ số lượng giác còn lại của a:
sin α = 0,8
cos α = 0,6
c) tan α = 3
d) cot α = 2
Bài 16. Cho góc nhọn α. Biết cos α – sin α = 1/5. Tính cot α.
Bài 17. Cho tam giác ABC vuông tại C. Biết cos A = 5/13. Tính tan B.
Bài 18. Rút gọn các biểu thức sau:
a) (1- cos α)(1 + cos α)
b) 1 + sin2 α cos2 α
c) sin α – sin α cos2 α
d) sin4 α + cos4 α + 2 sin2 α cos2 α
e) tan2 α – sin2 α tan2 α
f) cos2 α + tan2 α cos2 α
Bài 19. Chứng minh các hệ thức sau:
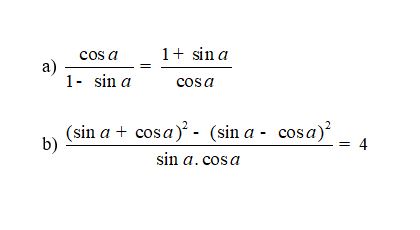
Bài 20. Cho tam giác nhọn ABC. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C.
a) Chứng minh: a/sin A = b/sin B = c/sin C.
b) Có thể xảy ra đẳng thức sin A = sin B + sin C không?
III. HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
1. Lý thuyết về cạnh và góc trong tam giác vuông

2. Bài tập vận dụng về cạnh và góc trong tam giác vuông
Bài 21. Giải tam giác vuông ABC, biết A = 90° và:
a) a = 15cm; b = 10cm
b) b = 12cm; b = 7cm
Bài 22. Cho tam giác ABC có B = 60°, C = 50°, AC = 35cm. Tính diện tích tam giác ABC.
Bài 23. Cho tứ giác ABCD có A = D = 90°, C = 40°, AB = 4cm, AD = 3cm. Tính diện tích tứ giác ABCD.
Bài 24. Cho tứ giác ABCD có các đường chéo cắt nhau tại O. Cho biết AC = 4cm, BD = 5cm, AOB = 50°. Tính diện tích tứ giác ABCD.
Bài 25. Chứng minh rằng:
a) Diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy.
b) Diện tích của một hình bình hành bằng tích của hai cạnh kề nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy.
IV. BÀI ÔN TẬP VỀ HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 26. Cho tam giác ABC có AB = 21m, AC = 28m, BC = 35m.
a) Chứng minh tam giác ABC vuông.
b) Tính sin B, sin C.
Bài 27. Cho tam giác ABC vuông tại A, đường cao AH, đường phân giác AD. Cho biết HB = 112, HC = 63.
a) Tính độ dài AH. b) Tính độ dài AD.
Bài 28. Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 5, CH = 6.
a) Tính AB, AC, BC, B b) Tính diện tích tam giác ABC.
Bài 29. Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 16, BH = 25.
a) Tính AB, AC, BC, CH. b) Tính diện tích tam giác ABC.
Bài 30. Cho hình thang ABCD có và hai đường chéo vuông góc với nhau tại O.
a) Chứng minh hình thang này có chiều cao bằng trung bình nhân của hai đáy.
b) Cho AB = 9, CD = 16. Tính diện tích hình thang ABCD.
c) Tính độ dài các đoạn thẳng OA, OB, OC, OD.
Bài 31. Tính diện tích hình thang ABCD (AB // CD), biết AB = 10, CD = 27, AC = 12, BD = 35.
Bài 32. Cho biết chu vi của một tam giác bằng 120cm. Độ dài các cạnh tỉ lệ với 8, 15, 17.
a) Chứng minh rằng tam giác đó là một tam giác vuông.
b) Tính khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh.
HD: Gọi O là giao điểm ba đường phân giác. Diện tích tam giác ABC = Diện tích tam giác OBC + Diện tích tam giác OCA + Diện tích tam giác OAB.
Bài 33. Cho tam giác ABC cân tại A, đường cao AH. Biết A = 48°, AH = 13cm. Tính chu vi tam giác ABC.
Bài 34. Cho tam giác ABC vuông tại A, AB = a, AC = 3a. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.
a) Chứng minh DE/DB = DB/DC.
b) Chứng minh tam giác BDE đồng dạng với tam giác CDB.
c) Tính tổng AFB + BCD.
Hy vọng rằng bài viết về Hệ thức lượng trong tam giác vuông lớp 9 ở trên sẽ giúp các em nắm chắc lý thuyết, cách làm bài tập về hệ thức lượng trong tam giác vuông cũng như đạt điểm cao hơn trong các bài thi, bài kiểm tra môn Toán.
Đừng quên tham khảo thêm 2 cuốn Làm chủ kiến thức Toán 9 ôn thi vào 10 phần Đại số và Hình học để biết cách giải tất cả các bài toán trong chương trình lớp 9 nhé!
Link đọc thử phần Đại số: https://drive.google.com/file/d/1uaOJCek1Mpmm-UbFU3hEIVzQ0P6PPaoC/view
Link đọc thử phần Hình học: https://drive.google.com/file/d/162Yv0A_lC8XmgSN_AjwxVuKPWpbVVkJj/view
Nếu các em có bất kỳ thắc mắc nào, hãy để lại bình luận dưới bài viết để được giải đáp nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 9 hàng đầu tại Việt Nam!


