Chưa có sản phẩm trong giỏ hàng.
Hàm số bậc 1 – Lý thuyết, các dạng toán và cách giải cực chi tiết
Hàm số bậc 1 là kiến thức quan trọng trong chương trình lớp 9. Dưới đây là tất cả những kiến thức cần nhớ về hàm số bậc 1 bao gồm lý thuyết, các dạng toán và cách giải.
Mời các bạn tham khảo!
I. Hàm số bậc 1 là gì?
| – Hàm số bậc 1 (bậc nhất) là hàm số có dạng y = ax + b với a ≠ 0. – Hàm số bậc nhất y = ax + b (a ≠ 0) xác định với ∀x ∈ R. Trên lập số thực R, hàm số đồng biến khi a = 0, hàm số nghịch biến khi a < 0. – Đồ thị hàm số y = ax + b (a ≠ 0) là đường thẳng song song với đường thẳng y = ax và cắt trục tung tại điểm có tung độ bằng b. – Khi a = 0, góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn. Khi a < 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù. – Xét hai đường thẳng (d): y = ax + b (a ≠ 0) và (d’): y=a’x + b; (a’ ≠ 0) Ta có:
– Hàm số y = ax 2 (a ≠0) xác định với ∀x ∈ R. Nếu a = 0 thì hàm số đồng biến khi x ≥ 0; nghịch biến khi x < 0; bằng 0 khi x = 0. Nếu a < 0, hàm số đồng biến khi x < 0; nghịch biến khi x > 0 ; bằng 0 khi x = 0. – Đồ thị hàm số y = ax 2 (a ≠ 0) là một parabol đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. – Cho đường thẳng (d) y = mx + n và parabol (P) y = ax 2 (a ≠ 0). – Xét phương trình ax 2 = mx + n ⇔ ax 2 – mx – n = 0 (1)
|
II. Các dạng toán cơ bản về hàm số bậc 1 và cách giải
1. Dạng 1: Nhận dạng hàm số bậc 1
+ Phương pháp
Hàm số bậc nhất là hàm số có dạng y = ax + b với a ≠ 0.
– Để tìm hàm số bậc nhất, ta xác định đó là hàm số một biến (có bậc là 1) và đưa về dạng y = ax + b với hệ số a ≠ 0.

+ Các ví dụ
- Ví dụ 1:
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Xác định các hệ số a,b của hàm số bậc nhất.
a) y = 5 – 3x;
b) y = 10x² – 9;
c) y = 3(x-1) – x;
d) y = x³ + 1;
e) y = (x + 1)/√3
f) y = 1 – (4x + 1)/3;
g) y = 1/x + x
h) y = 2(x – 1) + √3
- Lời giải:
Các hàm số bậc nhất là a, c, e, f, h.
a) Hàm số y = − 3x + 5 là hàm số bậc nhất, có hệ số a = – 3, b = 5.
c) y = 2x – 3;
e) y = (1/√3)x + 1/√3
f) y = (-4/3)x + 2/3
h) y = √2x + √3 – √2
2. Dạng 2: Tìm tham số m để hàm số là hàm số bậc 1
+ Phương pháp
Để hàm số là hàm số bậc nhất, ta làm như sau:
Bước 1: Đưa hàm số đã cho về dạng y = ax + b và tìm hệ số a của hàm số đó.
Bước 2: Cho a = 0, ta tìm được điều kiện của tham số m.
Nhận xét: Nếu hàm số có dạng y = ax + bx + c thì để hàm số là hàm số bậc nhất, ta xét a = 0 và b = 0.
+ Các ví dụ
- Ví dụ 2:
Tìm tất cả các giá trị của tham số m để các hàm số sau là hàm số bậc nhất.
a) y = (2m – 3)x – 1;
b) y = √(m – 2) (x – 1);
c) y = [(√m +1)/(√m – 1)] x + 1;
d) y = m(1 – x) + m – x;
- Lời giải:
a) y = (2m – 3)x−1 là hàm số bậc nhất khi 2m – 3 ≠ 0 ⇔ m ≠ (3/2)
b) y = √(m – 2)x – √(m – 2) là hàm số bậc nhất khi √(m – 2) ≠0 ⇔ m > 2.
c) y = [(√m +1)/(√m – 1)] x + 1 là hàm số bậc nhất khi m ≥ 0 và m ≠ 1.
d) y = –(m+1)x + 2m là hàm số bậc nhất khi m ≠ −1.
3. Dạng 3: Xét tính đồng biến, nghịch biến của hàm số bậc 1
+ Phương pháp
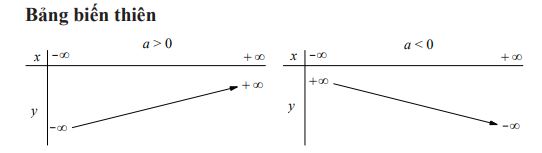
Hàm số bậc nhất y = ax + b (a ≠ 0) xác định với mọi x ∈ R, ta có:
- Đồng biến trên R nếu a > 0.
- Nghịch biến trên R nếu a < 0.
+ Các ví dụ
- Ví dụ 4:
Trong hai hàm số y = 2x – 4 và y = −3x + 5. Hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
- Lời giải:
Hàm số y = 2x – 4 đồng biến vì a = 2 > 0.
Hàm số y = –3x + 5 nghịch biến vì a = −3 < 0.
- Ví dụ 5: Tìm m để các hàm số sau đồng biến trên R:
a) y = (m-1)x + m;
b) y = (4m² -1)x – 2;
- Lời giải:
a) Hàm số y = (m−1)x + m đồng biến trên R khi m – 1 > 0 ⇔ m > 1.
b) Hàm số y = (4m² -1)x – 2 đồng biến trên R khi m > ½ hoặc m < -½ .
4. Dạng 4: Vẽ đồ thị của hàm số bậc 1
+ Phương pháp
Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng:
- Cắt trục tung tại điểm có tung độ bằng b.
- Cắt trục hoành tại điểm có hoành bằng -b/a
Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0):
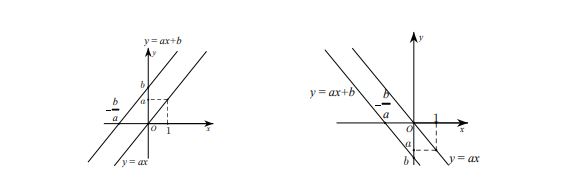
- Nếu b = 0 thì y = ax. Đồ thị của hàm số y = ax là đường thẳng đi qua gốc toạ độ O(0;0) và điểm A(1;a).
- Nếu b = 0 thì đồ thị y = ax + b là đường thẳng đi qua các điểm A(0;b) và B(- ;0).
+ Các bước thực hiện:
- Bước 1:
Cho x = 0 => y = b, ta được điểm A(0;b).
Cho y = 0 => x = -b/a ta được điểm B (-b/a;0).
- Bước 2:
Vẽ đường thẳng đi qua hai điểm A và B ta được đồ thị của hàm số y = ax + b.
+ Tìm tọa độ giao điểm của hai đường thẳng (phương pháp đại số):
Cho hai đường thẳng (d): y = ax + b và (d): y = a’x + b’.
- Bước 1: Xét phương trình hoành độ giao điểm của (d) và (d): ax + b = a’x + b’.
- Bước 2: Tìm x từ phương trình hoành độ giao điểm trên và thay vào phương trình của (d) hoặc (d’) để tìm y.
- Bước 3: Kết luận tọa độ giao điểm của (d) và (d’) là (x;y) vừa tìm được.
+ Ví dụ 1: Vẽ đồ thị hàm số y = x – 3.
- Lời giải:
Cho x = 0 => y = – 3, ta được điểm A(0;-3) thuộc đồ thị hàm số số y = x – 3.
Cho y = 0 => x = 3, ta được điểm B(3;0) thuộc đồ thị hàm số y = x – 3.
Vậy đồ thị hàm số y = x − 3 là đường thẳng đi qua hai điểm A và B.
+ Ví dụ 2: Cho hai đường thẳng (d1): y = 2x và (d2): y = -x + 3
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ.
b) Điểm A(1;2) có thuộc (d1) và (d2) không? Vì sao?
- Lời giải:
- a) Đồ thị hàm số (d1): y = 2x là đường thẳng đi qua hai điểm 0(0;0) và A(1;2). Đồ thị hàm số y = -x + 3 là đường thăng đi qua hai điểm B(0;3) và C(3;0).
- b) Tọa độ M(1;2) thỏa mãn (d1) và (d2) => A € (d1) và A € (d2).
Các dạng toán khác về hàm số bậc nhất được ghi chú và diễn giải rất đầy đủ trong cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.


