Chưa có sản phẩm trong giỏ hàng.
Giới hạn của dãy số – Lý thuyết, bài tập và cách giải cực chi tiết
Giới hạn của dãy số là kiến thức quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 5% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.
Dưới đây là toàn bộ kiến thức về giới hạn của dãy số. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
1. Giới hạn hữu hạn của dãy số
a. Định nghĩa
Định nghĩa 1
Ta nói dãy số (un) có giới hạn là 0 khi n dần tới dương vô cực, nếu |un| có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
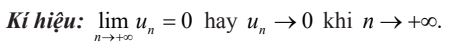

Định nghĩa 2
Ta nói dãy số (vn) có giới hạn là a (hay vn dần tới a) khi:
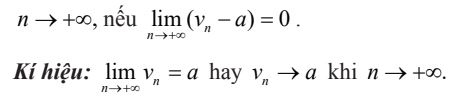

b. Một vài giới hạn đặc biệt
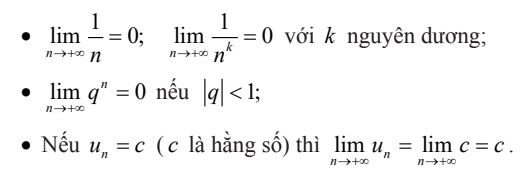
Chú ý: Từ nay về sau ta viết tắt giới hạn của dãy số là lim un = a.

2. Định lí về giới hạn hữu hạn
Định lí 1
a. Nếu lim un = a và lim vn = b thì:
- lim (un + vn) = a + b.
- lim(un.vn) = a.b.
- lim (un + vn) = a – b.
- lim (un/vn) = a/b (nếu b ≠ 0).
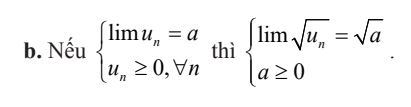
3. Tổng của cấp số nhân lùi vô hạn
Cấp số nhân vô hạn (un) có công bội q, với |q| < 1 được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn:
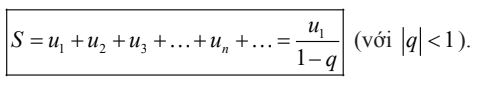

4. Giới hạn vô cực
a. Định nghĩa
Ta nói dãy số (un) có giới hạn là +∞ khi n → +∞, nếu un có thể lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi.
Kí hiệu: lim un = +∞ hay un → +∞ khi n→ +∞.
Dãy số (un) có giới hạn là -∞ khi n → +∞, nếu lim(-un) = +∞.
Kí hiệu: limun = -∞ hay un →-∞ khi n→ +∞.
- Nhận xét: un = +∞ ⟺ lim(-un) = -∞.

b. Một vài giới hạn đặc biệt
Ta thừa nhận các kết quả sau:
lim nk = +∞ với k nguyên dương,
limqn = +∞ nếu q>1.
c. Định lí 2
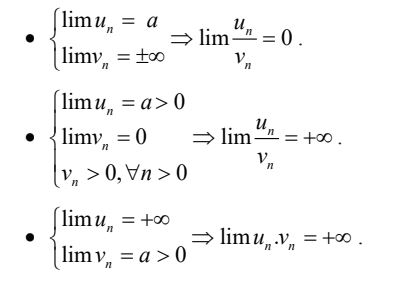
5. Bài tập về giới hạn của dãy số
Dưới đây là một số dạng toán cơ bản về Giới hạn của dãy số để các em luyện tập:

Các dạng toán khác về Giới hạn của dãy số được ghi chú và diễn giải rất đầy đủ trong cuốn cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.


