Chưa có sản phẩm trong giỏ hàng.
Đường thẳng và mặt phẳng trong không gian – Lý thuyết, bài tập và cách giải
Đường thẳng và mặt phẳng trong không gian là kiến thức quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.
Dưới đây là toàn bộ kiến thức về Đường thẳng và mặt phẳng trong không gian. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
I. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
1. Mở đầu về hình học không gian
Hình học không gian có các đối tượng cơ bản là điểm, đường thẳng và mặt phẳng.
Quan hệ thuộc: Trong không gian:
a) Với một điểm A và một đường thẳng d có thể хảy га hai trường hợp:
- Điểm A thuộc đường thẳng d, kí hiệu A∈d.
- Điểm A không thuộc đường thẳng, kí hiệu A ∉ d.
b) Với một điểm A và một mặt phẳng (P) có thể xảy ra hai trường hợp:
- Điểm A thuộc mặt phẳng (P), kí hiệu A∈(P)
- Điểm A không thuộc mặt phẳng (P), kí hiệu A∉ (P)
2. Các tính chất thừa nhận của hình học không gian
- Tính chất thừa nhận 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
- Tính chất thừa nhận 2: Có một và chỉ một mặt phăng đi qua ba điểm không thẳng hàng cho trước.
- Tính chất thừa nhận 3: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.
- Tính chất thừa nhận 4: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
- Tính chất thừa nhận 5: Trong mỗi mặt phẳng, các kết luận đã biết của hình học phẳng đều đúng.
Định lí: Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

3. Điều kiện xác định một phẳng
- Có bốn cách xác định trong một mặt phẳng:
- Cách 1: Một mặt phẳng được xác định nếu biết nó đi qua ba điểm A, B, C không thẳng hàng của mặt phẳng, kí hiệu (ABC)
- Cách 2: Một mặt phẳng được xác định nếu biết nó đi qua một đường thẳng d và một điểm A không thuộc d, kí hiệu (A,d) .
- Cách 3: Một mặt phẳng được xác định nếu biết nó đi qua hai đường thẳng a, b cắt nhau, kí hiệu (a,b).
- Cách 4: Một mặt phẳng được xác định nếu biết nó đi qua hai đường thẳng a, b song song, kí hiệu (a,b).

4. Hình chóp và tứ diện
Định nghĩa:: Cho đa giác A1A2,…An và cho điểm S nằm ngoài mặt phẳng chứa đa giác đó. Nối S với các đỉnh A1A2,…An ta được n miền đa giác SA1A2, SA2A3 … SAn-1An.
Hình gồm n tam giác đó và đa giác A1A2A3…An được gọi là hình chóp S.A1A2A3…An.\
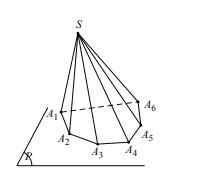
Trong đó:
- Điểm S gọi là đỉnh của hình chóp.
- Đa giác A1A2A3…An gọi là mặt đáy của hình chóp.
- Các đoạn thẳng A1A2, A2A3, …, An-1An gọi là các cạnh đáy của hình chóp.
- Các đoạn thẳng SA1, SA2, …, SAn gọi là các cạnh bên của hình chóp.
- Các miền tam giác SA1A2, SA2A3, …, SAn-1An gọi là các mặt bên của hình chóp.
Nếu đáy của hình chóp là một miền tam giác, tứ giác, ngũ giác thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,..
Chú ý:
- Hình chóp tam giác còn được gọi là hình tứ diện.
- Hình tứ diện có bốn mặt là những tam giác đều hay có tất cả các cạnh bằng nhau được gọi là hình tứ diện đều.

II. HAI ĐƯỜNG THẲNG CHÉO NHAU VÀ HAI ĐƯỜNG THẲNG SONG SONG
1. Vị trí tương đối của hai đường thẳng phân biệt
Cho hai đường thẳng a và b. Căn cứ vào sự đồng phẳng và số điểm chung của hai đường thẳng ta có bốn trường hợp sau:
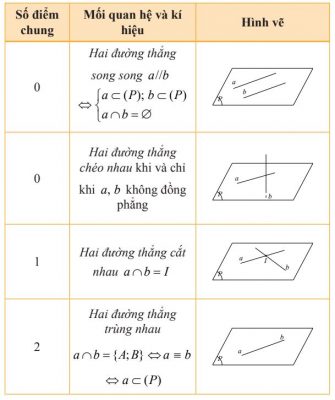
2. Hai đường thẳng song song
- Tính chất 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó.
- Tính chất 2: Hai đường thăng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Định lí (về giao tuyến của hai mặt phẳng): Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.
Hệ quả: Nếu hai mặt phẳng lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó (hoặc trùng với một trong hai đường thẳng đó).

III. ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG
1. Vị trí tương đối của đường thẳng và mặt phẳng
Cho đường thẳng a và mặt phẳng (P). Căn cứ vào số điểm chung của đường thẳng và mặt phẳng ta có ba trường hợp sau:
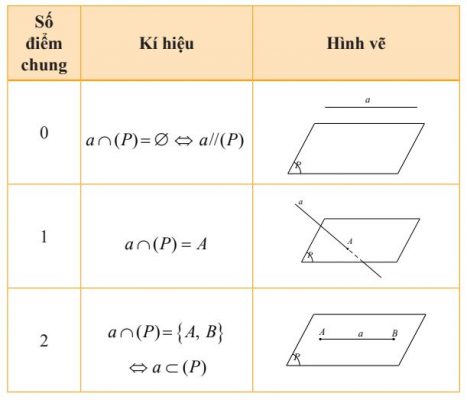

2. Điều kiện để một đường thẳng song song với một mặt phẳng
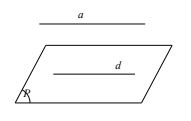
Định lí 1: Nếu đường thẳng a không nằm trong mặt phăng (P) và song song với một đường thẳng nào đó trong (P) thì a song song với (P).
Tức là, a ⊄ (P) thì nếu: a // d ⊂ (P) ⇒ a // (P).
3. Tính chất
Định lí 2: Nếu đường thẳng a song song với mặt phẳng (P) thì mọi mặt phẳng (Q) chứa a mà cắt (P) thì sẽ cắt theo một giao tuyến song song với a.
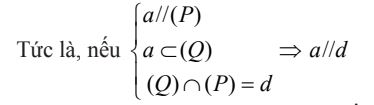
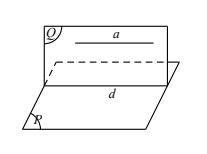
Hệ quả 1: Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thăng nào đó trong mặt phẳng.
Hệ quả 2: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến (nếu có) của chúng song song với đường thẳng đó.
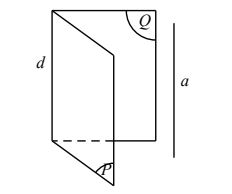
Hệ quả 3: Nếu a và b là hai đường thẳng chéo nhau thì qua a có một và chỉ một mặt phẳng song song với b.
IV. HAI MẶT PHẲNG SONG SONG
1. Vị trí tương đối của hai mặt phẳng phân biệt
Cho 2 mặt phẳng (P) và (Q). Căn cứ vào số đường thẳng chung của 2 mặt phẳng ta có ba trường hợp sau:
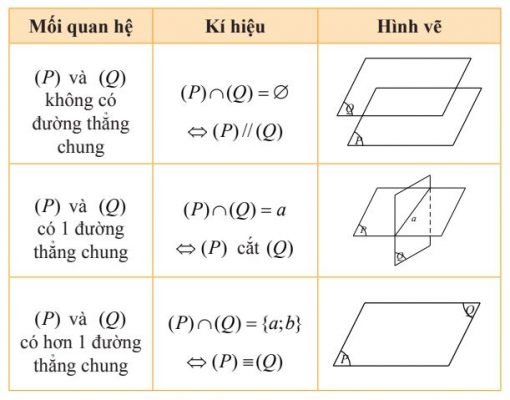
2. Điều kiện để hai mặt phẳng song song
Định lí 1: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
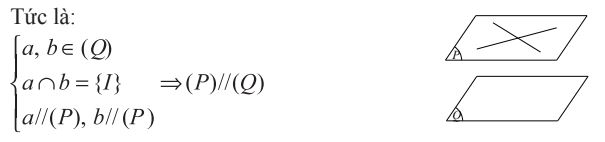
3. Tính chất
Tính chất 1: Qua một điểm nằm ngoài một mặt phẳng, có một và chỉ một mặt phẳng song song với mặt phẳng đó.
Tức là: O ∉ (P) ⇒ ∃ 1 (Q):
Cách dựng:
- B1: Trong (P) dựng a, b cắt nhau.
- B2: Qua O dựng
- B3: Mặt phẳng (a1,b1) là mặt phẳng qua O và song song với (P).
Hệ quả 1: Nếu đường thẳng a song song với mặt phẳng (Q) thì qua a có một và chỉ một mặt phẳng (P) song song với (Q) .
Hệ quả 2:: Hai mặt phăng phân biệt cùng song song với một mặt phẳng thứ ba thì song song với nhau.
Tính chất 2: Nếu hai mặt phẳng (P) và (Q) song song thì mặt phẳng (R) đã cắt (P) thì phải cắt (Q) và các giao tuyến của chúng song song.
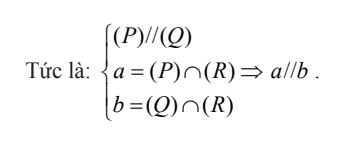
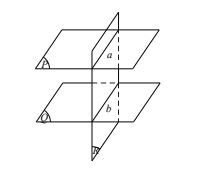
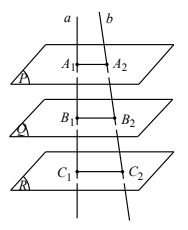
Định lí Ta – lét trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỷ lệ.
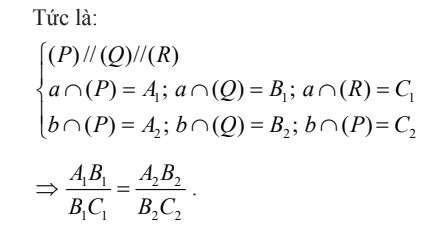
4. Hình lăng trụ và hình hộp
Định nghĩa hình lăng trụ: Hình lăng trụ là một hình đa diện có hai mặt nằm trong hai mặt phẳng song song gọi là hai đáy và tất cả các cạnh không thuộc hai cạnh đáy đều song song với nhau.
Trong đó:
- Các mặt khác với hai đáy gọi là các mặt bên của hình lăng trụ.
- Cạnh chung của hai mặt bên gọi là cạnh bên của hình lăng trụ.
Tùy theo đa giác đáy, ta có hình lăng trụ tam giác, lăng trụ tứ giác
Từ định nghĩa của hình lăng trụ, ta lân lượt suy ra các tính chất sau:
+ Các cạnh bên song song và bằng nhau.
+ Các mặt bên và các mặt chéo là những hình bình hành.
+ Hai đáy là hai đa giác có các cạnh tương ứng song song và bằng nhau.
Định nghĩa hình hộp: Hình lăng trụ có đáy là hình bình hành gọi là hình hộp.
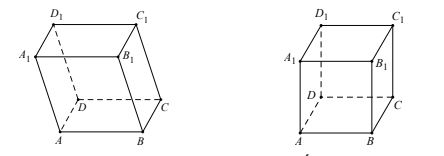
+ Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình chữ nhật gọi là hình hộp chữ nhật.
+ Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình vuông gọi là hình lập phương.
Chú ý: Các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường.
5. Hình chóp cụt
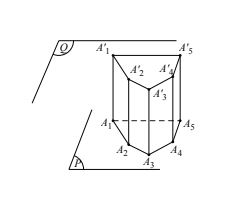
Định nghĩa: Cho hình chóp S.A1A2 …An. Một mặt phẳng (P) song song với mặt phẳng chứa đa giác đáy cắt các cạnh SA1, SA2, …, SAn theo thứ tự tại A1’, A2’, …, An’.
Hình tạo bởi thiết diện A1’A2’…An’ và đáy A1A2 …An của hình chóp cùng với các mặt bên A1A2 A1’A2’, A2A3 A3’A2’, An’A1’A1’An’ gọi là một hình chóp cụt.
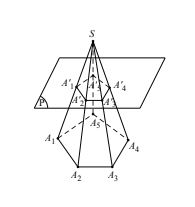
Trong đó:
- Đáy của hình chóp gọi là đáy lớn của hình chóp cụt, còn thiết diện gọi là đáy nhỏ của hình chóp cụt.
- Các mặt còn lại gọi là các mặt bên của hình chóp cụt.
- Cạnh chung của hai mặt bên kề nhau như AA1’, AA2’ …. AAn’ gọi là cạnh bên của hình chóp cụt.
Tùy theo đáy là tam giác, tứ giác, ngũ giác,… ta có hình chóp cụt tam giác, hình chóp cụt tứ giác, hình chụp cụt ngũ giác, …
Tính chất: Với hình chóp cụt, ta có các tính chất sau:
+ Hai đáy của hình chóp cụt là hai đa giác đồng dạng.
+ Các mặt bên của hình chóp cụt là các hình thang
+ Các cạnh bên của hình chóp cụt đồng quy tại một điểm.
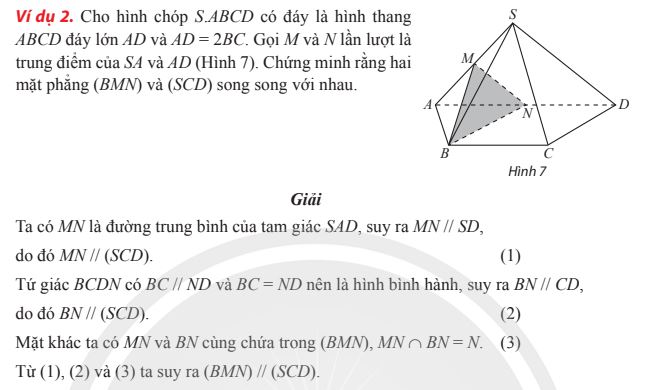
V. Bài tập về đường thẳng và mặt phẳng trong không gian
Dưới đây là một số dạng toán cơ bản về Đường thẳng và mặt phẳng trong không gian để các em luyện tập:

Các dạng toán khác về Đường thẳng và mặt phẳng trong không gian được ghi chú và diễn giải rất đầy đủ trong cuốn cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.