Chưa có sản phẩm trong giỏ hàng.
Cung và góc lượng giác – Lý thuyết, bài tập và cách giải cực chi tiết
Cung và góc lượng giác là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.
Dưới đây là toàn bộ kiến thức về cung và góc lượng giác. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
I. KHÁI NIỆM CUNG VÀ GÓC LƯỢNG GIÁC
1. Đường tròn định hướng và cung lượng giác
Đường tròn định hướng là một đường tròn trên đó ta chọn một chiều chuyển động gọi là chiều dương, chiều ngược lại là chiều âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ làm chiều dương.
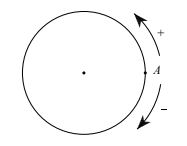
Trên đường tròn định hướng cho hai điểm A và B . Một điểm M di động trên đường tròn luôn theo một chiều (âm hoặc dương) từ A đến B tạo nên một cung lượng giác có điểm đầu A điểm cuối B.
Với hai điểm A, B đã cho trên đường tròn định hướng ta có vô số cung lượng giác điểm đầu A, điểm cuối B . Mỗi số cung như vậy đều được kí hiệu là ↷AB.
2. Góc lượng giác
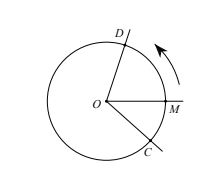
Trên đường tròn định hướng cho một cung lượng giác ↷CD . Một điểm M chuyển động trên đường tròn từ C tới D tạo nên cung lượng giác ↷CD nói trên.
Khi đó tia OM quay xung quanh gốc 0 từ vị trí OC tới vị trí OD . Ta nói tia OM tạo ra một góc lượng giác, có tia đầu là OC, tia cuối là OD.
Kí hiệu góc lượng giác đó là (OC,OD).
3. Đường tròn lượng giác
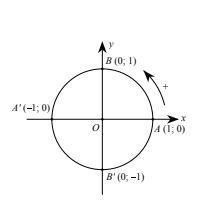
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn định hướng tâm O bán kính R=1.
Đường tròn này cắt hai trục tọa độ tại bốn điểm A(1;0), A’(−1;0), B(0;1),B'(0;-1).
Ta lấy A(1;0) làm điểm gốc của đường tròn đó.
Đường tròn xác định như trên được gọi là đường tròn lượng giác (gốc A).
II. SỐ ĐO CỦA CUNG VÀ GÓC LƯỢNG GIÁC
1. Độ và radian
a. Đơn vị radian
Trên đường tròn tùy ý, cung có độ dài bằng bán kính được gọi là cung có số đo 1 rad.
b. Quan hệ giữa độ và radian

c. Độ dài của một cung tròn
Trên đường tròn bán kính R, cung nửa đường tròn có số đo là π rad và có độ dài là π R . Vậy cung có số đo α rad của đường tròn bán kính R có độ dài:
ℓ = Rα
2. Số đo của một cung lượng giác
Số đo của một cung lượng giác ↷AM ( A ≠ M ) là một số thực âm hay dương.
Kí hiệu số đo của cung ↷AM là Sđ ↷AM
Ghi nhớ: Số đo của các cung lượng giác có cùng điểm đầu và điểm cuối sai khác nhau một bội của 2π .
Ta viết:
Sđ ↷AM = α + k2π, k ∈ Z
trong đó α là số đo của một cung lượng giác tùy ý có điểm đầu là A, điểm cuối là M.
3. Số đo của một góc lượng giác
Số đo của góc lượng giác (OA,OC) là số đo của cung lượng giác ↷AC tương ứng.
Chú ý:
Vì mỗi cung lượng giác ứng với một góc lượng giác và ngược lại, đồng thời số đo của các cung và góc lượng giác tương ứng là trùng nhau, nên từ nay về sau khi ta nói về cung thì điều đó cũng đúng cho góc và ngược lại.
4. Biểu diễn cung lượng giác trên đường tròn lượng giác
Chọn điểm gốc A(1;0) làm điểm đầu của tất cả các cung lượng giác trên đường tròn lượng giác. Để biểu diễn cung lượng giác có số đo a trên đường tròn lượng giác ta cần chọn điểm cuối M của cung này. Điểm cuối M được xác định bởi hệ thức
Sđ ↷AM = α
III. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT CUNG
1. Giá trị lượng giác của cung α
a. Định nghĩa
Trên đường tròn lượng giác cho cung ↷AM có Sđ AM = α (còn viết ↷AM = α )

Các giá trị sin α, cos α, tan α, cot α được gọi là các giá trị lượng giác của cung α.
Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin.
b. Hệ quả
sin α và cos α xác định với mọi a ∈ R . Hơn nữa, ta có:
sin(α + k2π) = sin α, ∀k ∈ Z
cos(α + k2π) = cos α, ∀k ∈ Z
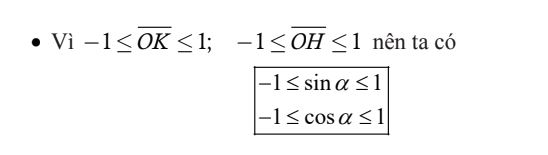
Với mọi m ∈ R mà -1 ≤ m ≤ 1 đều tồn tại α và β sao cho sin α = m và cos β = m
tan α xác định với mọi α ≠π/2 + kπ, k∈Z
cot α xác định với mọi α ≠kπ, k∈Z
Dấu của các giá trị lượng giác của góc α phụ thuộc vào vị trí điểm cuối của cung AM = α trên đường tròn lượng giác.
Bảng xác định dấu của các giá trị lượng giác:
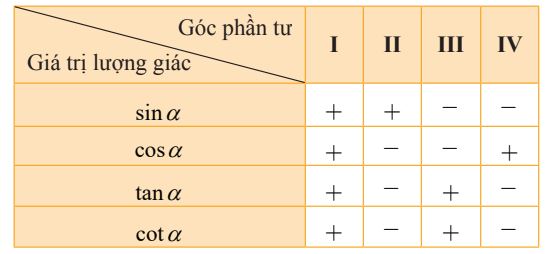
c. Giá trị lượng giác của các cung đặc biệt
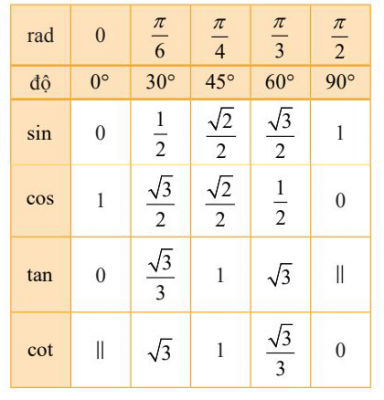
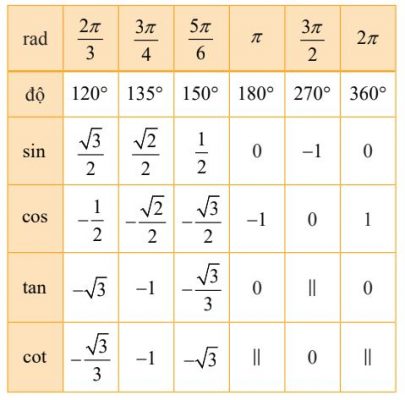
Chú thích: Kí hiệu “||” tức là không xác định.
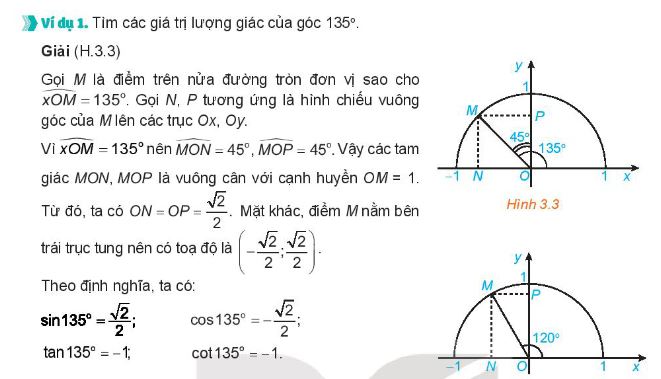
2. Ý nghĩa hình học của tang, cotang
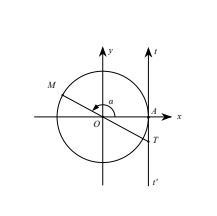
a. Ý nghĩa hình học của tan α
Từ A vẽ tiếp tuyến tA’t với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại A.
Gọi T là giao điểm của OM với trục t’At. tan α được biểu diễn bởi độ dài đại số của vectơ AT trên trục t’At . Trục t’At được gọi là trục tang.
b. Ý nghĩa hình học của cot α
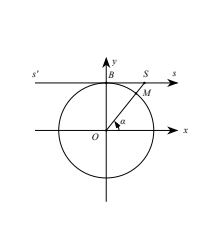
Từ B vẽ tiếp tuyến s’Bs với đường tròn lượng giác.
Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại B
Gọi S là giao điểm của OM với trục s’Bs
cot α được biểu diễn bởi độ dài đại số của vectơ BS trên trục s’Bs . Trục s’Bs được gọi là trục côtang.
3. Quan hệ giữa các giá trị lượng giác
a. Công thức lượng giác cơ bản
Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau:
sin2 α + cos2 α = 1
1 + tan2 α = 1/( cos2 α), α ≠π/2 + kπ, k∈Z
1 + cot2 α = 1/( sin2 α), α ≠π/2 + kπ, k∈Z
tan α.cot α = 1, α ≠π/2 + kπ, k∈Z
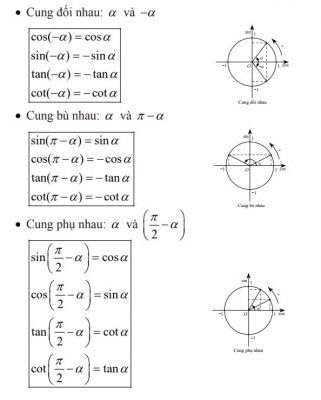
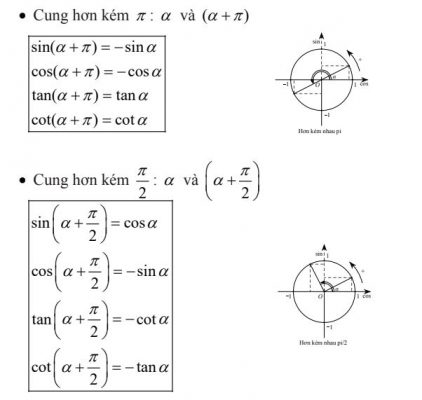
b. Giá trị lượng giác của các cung có liên quan đặc biệt “COS ĐỐI – SIN BÙ – PHỤ CHÉO, TAN – COT HƠN KÉM π
IV. CÔNG THỨC LƯỢNG GIÁC
1. Công thức cộng
cos(a – b) = cos a.cosb + sin a.sin b
cos(a + b) = cos a.cos b – sin a.sin b
sin(a – b) = sin a.cos b – cos a.sin b
sin(a+b) = sin a.cos b + cos a.sin b

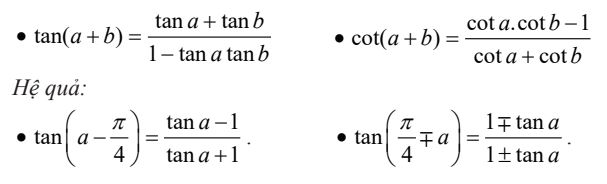
2. Công thức nhân đôi
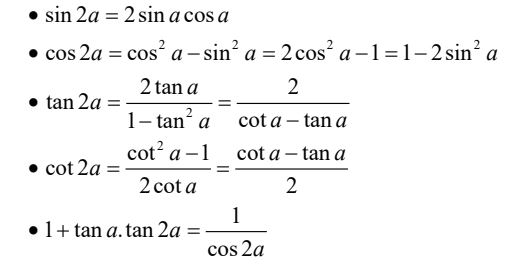
3. Công thức nhân ba
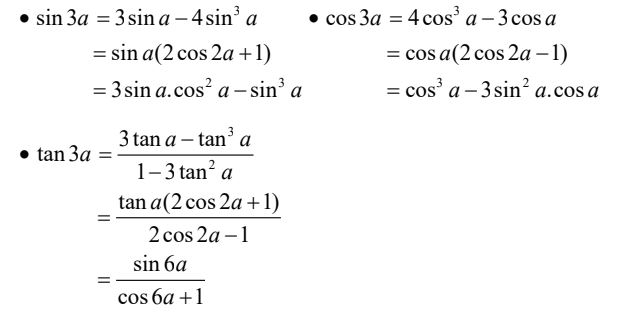
4. Công thức biến đổi tích thành tổng
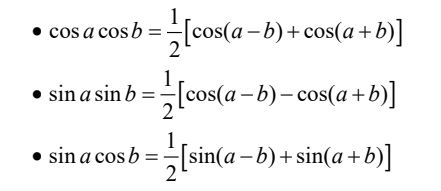
5. Công thức biến đổi tổng thành tích
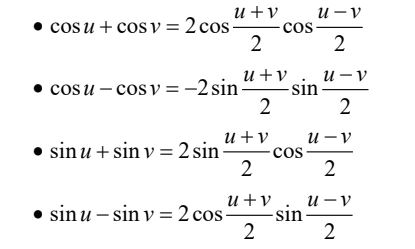
6. Một số công thức nâng cao khác
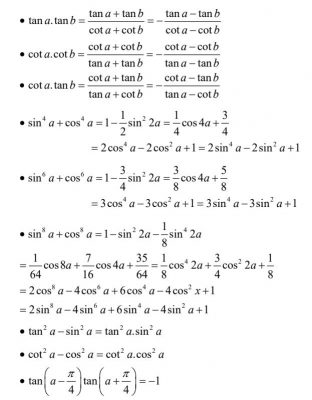
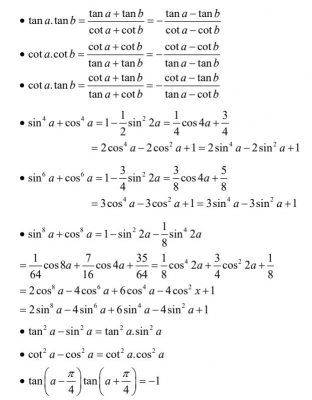
V. Một số bài tập về bất đẳng thức và bất phương trình
Dưới đây là một số dạng toán cơ bản về Cung và góc lượng giác để các em luyện tập và ôn luyện kiến thức:


VI. Cách tính giá trị lượng giác bằng máy tính
Các em có thể sử dụng máy tính cầm tay để tính đúng hoặc gần đúng các giá trị lượng giác theo hướng dẫn sau:

Các dạng toán khác về Cung và góc lượng giác được ghi chú và diễn giải rất đầy đủ trong cuốn cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.

