Chưa có sản phẩm trong giỏ hàng.
Công thức tổ hợp chỉnh hợp – Lý thuyết, bài tập và cách giải cực chi tiết
Công thức tổ hợp, chỉnh hợp là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.
Dưới đây là toàn bộ kiến thức về Công thức tổ hợp và chỉnh hợp. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
I. QUY TẮC ĐẾM
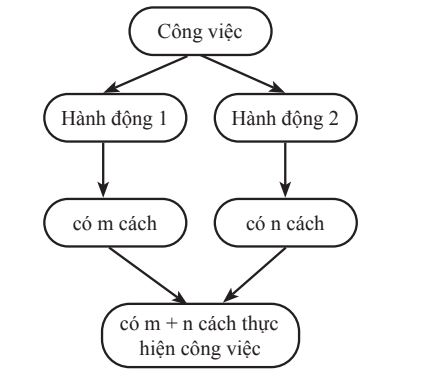
1. Quy tắc cộng
Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kỳ cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện.

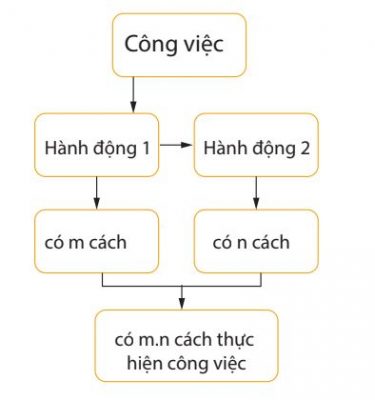
2. Quy tắc nhân
Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m × n cách hoàn thành công việc.
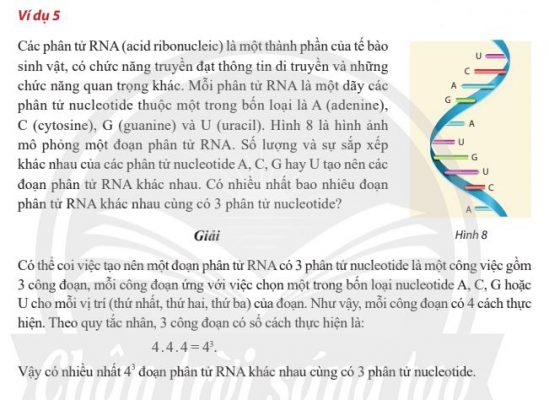
II. HOÁN VỊ – CHỈNH HỢP – TỔ HỢP
1. Hoán vị
a) Định nghĩa
Cho tập A gồm n phần tử (n ≥ 1).
Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.
b) Định lí
Số các hoán vị của n phần tử, kí hiệu là:
| P = n! = n(n-1).(n-2)…3.2.1 |
2. Chỉnh hợp
a) Định nghĩa
Cho tập hợp A gồm n phần tử (n ≥ 1).
Kết quả của việc lấy k (với 1 < k < n ) phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
b) Định lí
Số các chỉnh hợp chập k của một tập hợp có n phần tử là:
| Akn = n!/(n – k)! |
c) Một số qui ước
| 0! = 1; A0n = 1; Ann = n! = Pn |
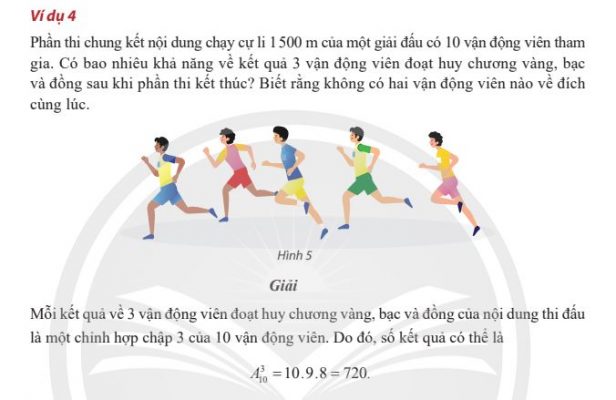
3. Tổ hợp
a) Định nghĩa
Giả sử tập hợp A có n phần tử (n ≥ 1).
Mỗi tập con gồm k (với 1 ≤ k ≤ n ) phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.
b) Định lí
Số các tổ hợp chập k của một tập có n phần tử là:
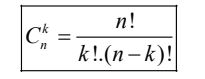
c) Một số qui ước
| C0n = 1; Cnn = 1 |
Với qui ước này ta có:
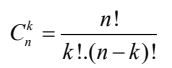
đúng với số nguyên dương k thỏa mãn 1 ≤ k ≤ n.
d) Tính chất
- Tính chất 1: Ckn = Cn-kn (với 0 ≤ k ≤ n).
- Tính chất 2: Ck – 1n – 1 = Ckn (với 1 ≤ k ≤ n).
- Tính chất 3: k.Ckn = n. Ck – 1n – 1
- Tính chất 4: (n+1).Ckn = (k + 1).Ck + 1n + 1

III. NHỊ THỨC NEW TON
1. Nhị thức Niu-tơn
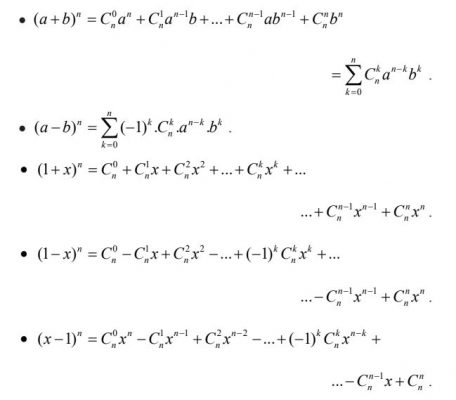
2. Hệ quả
- Với a = b =1.
Ta có 2n = C0n + C1n + … + Cn-1n + C”n.
- Với a = 1; b = -1.
Ta có 0n = C0n – C1n + … + (-1)kCkn + … + (-1)nC”n.
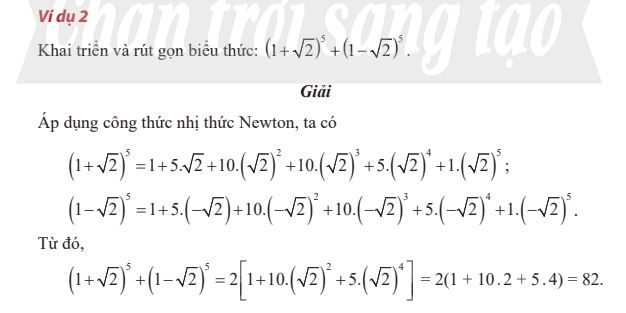
3. Chú ý
Trong biểu thức ở vế phải của khai triển (a + b)n:
- Số hạng tử là: n + 1;
- Các hạng tử có số mũ của a giảm dần từ n đến 0.
- Các hạng tử có số mũ của b tăng dần từ 0 đến n .
Tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước a0 = b0 =1);
- Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối đều bằng nhau.
- Số hạng thứ k +1 trong khai triển là Tk+1 = Ckn.an-k.bk
4. Khai triển tam thức
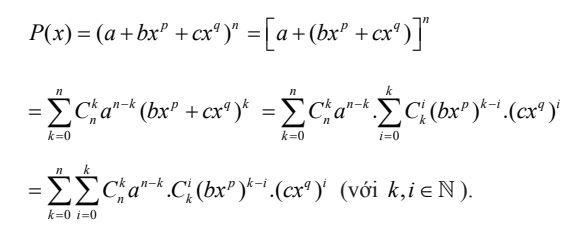
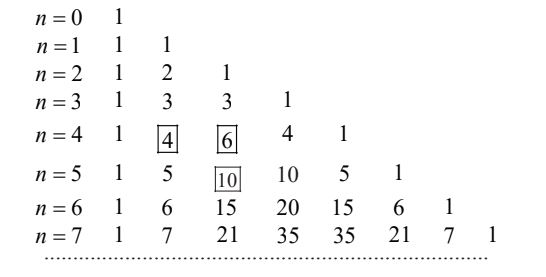
4. Tam giác Pasacal
Các hệ số của khai triển: (a + b)0, (a + b)1, (a + b)2, …, (a + b)n có thể xếp thành một tam giác gọi là tam giác PASCAL.
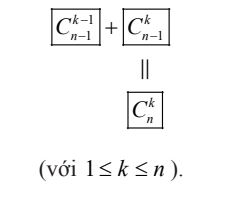
Hằng đẳng thức Pascal:
IV. MỘT SỐ DẠNG TOÁN KHÓ
Dạng 1: Tìm hệ số lớn nhất trong khai triển (a + bx)n
Phương pháp: Xét khai triển nhị thức Newton có số hạng tổng quát: Tk+1 = Ckn. an-k.bk.xk
Đặt ak = Ckn. an-k.bk (với 0 ≤ k ≤ n) thì dãy hệ số là {ak}.
Khi đó hệ số lớn nhất trong khai triển này thỏa mãn hệ phương trình:
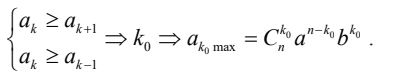
Dạng 2: Tìm số hạng hữu tỉ (hoặc số hạng là số nguyên) trong khai triển (a + b)n.
Phương pháp: Xét khai triển (a + b)n có số hạng tổng quát:
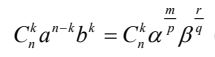
(với α, β là các số hữu tỉ).
Số hạng hữu tỉ cần tìm thỏa mãn hệ phương trình:
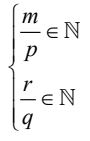
(với k∈N, 0 ≤ k ≤ n) => k0 => Ck0n.an-k0.bk0 là số hạng cần tìm.
V. Cách tính tổ hợp bằng máy tính cầm tay

VI. Bài tập luyện tập
Dưới đây là một số dạng toán cơ bản về Tổ hợp, chỉnh hợp và nhị thức Niu – tơn để các em luyện tập:
1. Bài tập tổ hợp, chỉnh hợp

2. Bài tập nhị thức Niu – tơn

Các dạng toán khác về Công thức tổ hợp chỉnh hợp được ghi chú và diễn giải rất đầy đủ trong cuốn cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.


