Chưa có sản phẩm trong giỏ hàng.
Cách chứng minh tứ giác nội tiếp trong đường tròn mới nhất
Cách chứng minh tứ giác nội tiếp trong đường tròn mới nhất dưới đây sẽ giúp các em nắm vững những quy tắc, định lý cơ bản và áp dụng chúng vào các bài tập chứng minh tứ giác nội tiếp thực tiễn.
Mời quý phụ huynh và các em tham khảo!
I. Phần lý thuyết
1. Định nghĩa tứ giác nội tiếp đường tròn:
Tứ giác có bốn định nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (hoặc đơn giản là tứ giác nội tiếp) và đường tròn được gọi là đường tròn ngoại tiếp tứ giác.
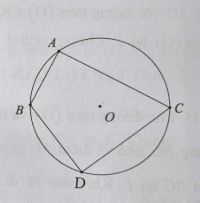
2. Định lí:
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180°.
3. Trường hợp đặc biệt:
Hình chữ nhật và hình vuông là các tứ giác nội tiếp. Đường tròn ngoại tiếp của chúng có tâm là giao điểm của hai đường chéo và bán kính bằng một nửa độ dài đường chéo.
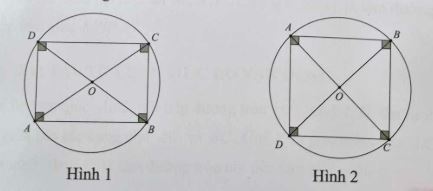
II. Cách chứng minh tứ giác nội tiếp trong đường tròn
1. Kiến thức cần sử dụng
+ Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn.
+ Hình chữ nhật và hình vuông là các tứ giác nội tiếp. Đường tròn ngoại tiếp của chúng có tâm là giao điểm của hai đường chéo và bán kính băng một nửa độ dài đường chéo.
+ Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền.
2. Cách chứng minh
Để chứng minh một tứ giác nội tiếp trong đường tròn, ta có thể sử dụng một số cách chứng minh cơ bản sau đây:
👉 Chứng minh hai góc đối diện bằng nhau:
Nếu một tứ giác nội tiếp trong đường tròn, thì tổng của hai góc đối diện luôn bằng 180°. Cách này sử dụng định lý “góc nội tiếp” của đường tròn.
Cụ thể, nếu tứ giác ABCD là tứ giác nội tiếp, ta chứng minh rằng:
- ∠ ABC +∠ ADC = 180°
- ∠ DAB +∠ BCD = 180°
Điều này chứng minh rằng tứ giác này là tứ giác nội tiếp, vì các cặp góc đối diện bằng nhau.
👉 Dùng định lý về đường tròn ngoại tiếp:
Một tứ giác có thể được chứng minh là tứ giác nội tiếp nếu như nó có một đường tròn ngoại tiếp. Điều này có thể thực hiện bằng cách chứng minh rằng ba điểm bất kỳ trong tứ giác nằm trên một đường tròn.
👉 Sử dụng định lý Ptolemy:
Định lý Ptolemy phát biểu rằng trong một tứ giác nội tiếp, tích của hai đường chéo phải bằng tổng tích của các cặp cạnh đối diện. Tức là nếu tứ giác ABCD nội tiếp trong đường tròn, ta có:
AC × BD = AB × CD + AD × BC
Chứng minh này có thể áp dụng khi ta biết rằng tứ giác là nội tiếp trong một đường tròn.
👉 Chứng minh qua các góc ở tâm:
Từ định lý về góc nội tiếp, ta có thể chứng minh rằng nếu các góc nội tiếp có mối quan hệ nhất định với nhau (như tổng góc đối diện bằng 180°), thì tứ giác đó là tứ giác nội tiếp.
Tùy theo bài toán cụ thể và những dữ liệu có sẵn, ta có thể chọn phương pháp chứng minh phù hợp.
III. Ví dụ
Cho tam giác ABC có đường cao AH và BK cắt nhau tại I . Chứng minh tứ giác ABHK và tứ giác IHCK nội tiếp. Xác định tâm và bán kinh của đường tròn ngoại tiếp các tứ giác trên.
Hướng dẫn giải:
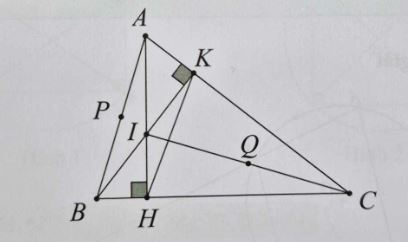
Gọi P là trung điểm của AB.
Xét tam giác ABK vuông tại K nên P là tâm đường tròn ngoại tiếp tam giác ABK do đó 3 điểm A, B, K cùng thuộc đường tròn (P;AB/2).
Tương tự ta có 3 điểm A,B, H cùng thuộc đường tròn (P;AB/2).
Do đó 4 điểm A,B,H,K cùng thuộc đường tròn (P;AB/2) nên tứ giác ABHK nội tiếp đường tròn (P;AB/2).
Gọi O là trung điểm của IC .
Xét tam giác IHC vuông tại H nên Q là tâm đường tròn ngoại tiếp tam giác THC do đó 3 điểm I, H,C cùng thuộc đường tròn (Q;IC/2).
Tương tự ta có 3 điểm I,K,C cùng thuộc đường tròn (Q;IC/2).
Do đó 4 điểm I,H,K,C cùng thuộc đường tròn (Q;IC/2) nên tứ giác IHCK nội tiếp đường tròn (Q;IC/2).
IV. Bài tập tự luyện
1. Bài tập trắc nghiệm
💦 Bài 1. Cho hình vẽ bên. Số đo ∠STU bằng:
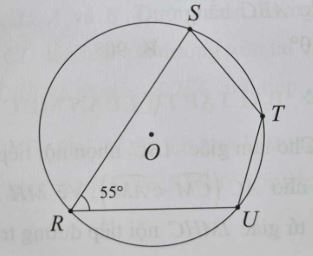
A. 125°.
B. 135°.
C. 145°.
D. 155°.
💦 Bài 2. Cho tứ giác ABCD nội tiếp đường tròn tâm O . Hai cạnh AD và BC cắt nhau tại E biết ∠CDE = 80° . Tính ∠ABC.
A. 100°.
B. 35°.
C. 80°.
D. 90°.
💦 Bài 3. Cho đường tròn tâm O. Từ điểm A bên ngoài đường tròn vẽ hai tiếp tuyến AB và AC (B,C là hai tiếp điểm). Bán kính đường tròn ngoại tiếp tứ giác ABOC là
A. OB.
B. OA.
C. OA/2
D. BC/2
💦 Bài 4. Cho tam giác ABC cân tại A có ∠BAC =120° . Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy D sao cho BCD là tam giác đều. Tâm đường tròn ngoại tiếp tứ giác ABDC là
A. Trung điểm cạnh AB.
B. Trung điểm cạnh AD.
C. Trung điểm cạnh AC.
D. Trung điểm cạnh BC.
💦 Bài 5. Cho hình vẽ dưới đây:
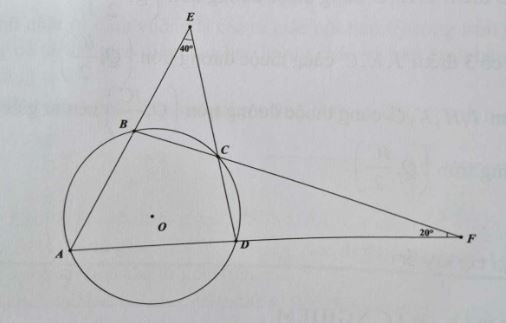
Số đo ∠ABC bằng:
A. 80°.
B. 90°
C. 100°
D. 110°
2. Bài tập tự luận mức độ cơ bản
💦 Bài 6. Cho tam giác ABC nhọn nội tiếp đường tròn (O) . M là điểm thuộc cung nhỏ AC(cung CM < cung AM). Vẽ MH ⊥ BC tại H, vẽ MI ⊥ AC tại I . Chứng minh tứ giác IMHC nội tiếp đường tròn.
💦 Bài 7. Bạn Lan dự định dùng chiếc khăn trải bàn hình tròn đường kính 1,2m cho chiếc bàn hình vuông có cạnh bằng 60cm . Bạn Lan có dùng được chiếc khăn phủ kín được mặt bàn không?
💦 Bài 8. Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Chứng minh tứ giác ABCD nội tiếp.
💦 Bài 9. Cho đường tròn (O) đường kính AB. Gọi I là điểm nằm giữa O và B. Kẻ dây CD ⊥AB tại H . Trên cung nhỏ AC lấy điểm E, kẻ CK ⊥ AE tại K . Xác định tâm và bán kính đường tròn ngoại tiếp tứ giác AHCK.
3. Bài tập tự luận mức độ nâng cao
💦 Bài 10. Cho tam giác ABC vuông tại A. Từ điểm H trên đoạn BC kẻ HM, HN lần lượt vuông góc với AB, AC . Chứng minh tứ giác AMHN nội tiếp đường tròn. Xác định tâm và bán kính đường tròn đó.
💦 Bài 11. Cho tam giác ABC cân tại A nội tiếp đường tròn (O) và ∠A = α (0° < α < 90°). Gọi M là một điểm tùy ý trên cung nhỏ AC, vẽ tia Bx vuông góc với AM cắt tia CM tại D . Tính số đo góc BDM .
💦 Bài 12. Cho đường tròn (O) đường kính AB . Gọi I là trung điểm của OA . Dây CD vuông góc với AB tại I. Lấy K tùy ý trên cung BC nhỏ, AK cắt CD tại H . Chứng minh tứ giác BIHK nội tiếp.
💦 Bài 13. Cho tam giác ABC vuông tại A và D nằm giữa A và B . Đường tròn đường kính BD cắt BC tại E. Các đường thẳng CD lần lượt cắt đường tròn tại các điểm thứ hai là F. Chứng minh tứ giác ACBF và tứ giác ADEC nội tiếp.
💦 Bài 14. Cho hình chữ nhật ABCD có AB = 2AD. Gọi M, N lần lượt là trung điểm của AB và DC. Chứng minh các tứ giác AMND và BMNC nội tiếp.
Phần đáp án của các bài tập trên, các em có thể xem trên App Tkbooks bằng cách quét mã QR đằng sau cuốn Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 9 – Luyện thi vào 10: Phần hình học và xác suất nhé!
Link đọc thử sách: https://drive.google.com/file/d/1UHkC2jakWiCOF0anlUXmljMBAsWgRQEo/view
Hy vọng bài viết trên đã giúp các em nắm bắt được các phương pháp chứng minh tứ giác nội tiếp trong đường tròn một cách rõ ràng và dễ hiểu, từ đó sẽ giải quyết nhanh được các bài tập liên quan và đạt điểm số cao hơn trong các bài thi, bài kiểm tra.


