Chưa có sản phẩm trong giỏ hàng.
Cách chứng minh 3 điểm thẳng hàng lớp 7, 8, 9 PDF
Cách chứng minh 3 điểm thẳng hàng lớp 7, 8, 9 PDF dưới đây sẽ hướng dẫn cho các em các phương pháp chứng minh ba điểm thẳng hàng từ cơ bản đến nâng cao trong chương trình học từ lớp 7 đến lớp 9.
Mời các em tham khảo! Nhớ tải file PDF để dễ dàng tham khảo và sử dụng mọi lúc, mọi nơi nhé!
I. Cách chứng minh ba điểm thẳng hàng lớp 7
1. Sử dụng góc:
🍀 Nguyên lý:
- Nếu ba điểm A,B,C nằm trên một đường thẳng, thì:
- Góc giữa các đoạn thẳng AB và BC bằng 180 độ.
- Tổng các góc trong tam giác ABC bằng 0 độ vì tam giác đó không tồn tại (các đỉnh nằm trên cùng một đường thẳng).
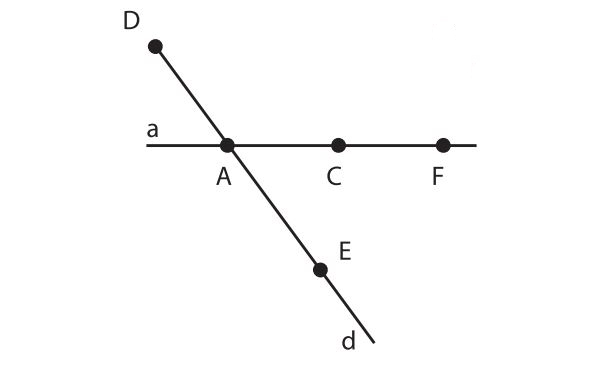
🍀 Phương pháp chứng minh:
♦ Cách 1: Sử dụng góc kề bù
- Bước 1: Xác định ba điểm A, B, C.
- Bước 2: Chứng minh rằng hai góc tạo bởi các đoạn thẳng AB và BC là góc kề bù.
Ví dụ: Nếu ∠ABC + ∠CBA = 180 độ thì ba điểm thẳng hàng.
- Kết luận: Theo định nghĩa góc kề bù, ba điểm nằm trên cùng một đường thẳng.
♦ Cách 2: Sử dụng góc bẹt
- Bước 1: Xác định ba điểm A, B, C.
- Bước 2: Tính góc tạo bởi hai đoạn thẳng AB và BC.
Nếu góc ∠ABC = 180 độ thì ba điểm nằm trên cùng một đường thẳng.
- Kết luận: Ba điểm thẳng hàng vì chúng tạo góc bẹt.
♦ Cách 3: Cộng góc trong tam giác bằng 0 độ
- Bước 1: Giả sử ba điểm A, B, C không thẳng hàng.
- Bước 2: Tính tổng ba góc ∠ABC, ∠BCA, và ∠CAB.
Nếu tổng bằng 0 độ thì tam giác không tồn tại, và ba điểm thẳng hàng.
2. Sử dụng tính đồng quy:
🍀 Nguyên lý:
Ba điểm A, B, C thẳng hàng nếu chúng nằm trên cùng một đường thẳng. Điều này có nghĩa là:
- Chúng đồng quy tại một đường thẳng duy nhất.
- Mọi đoạn thẳng nối giữa hai điểm bất kỳ trong ba điểm đều nằm trên cùng một đường thẳng.
- Các điểm cùng nằm trên một đường thẳng nếu chúng đồng quy tại một đường thẳng.
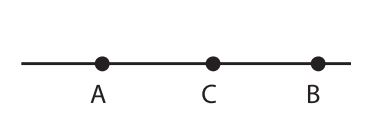
🍀 Phương pháp chứng minh bằng tính đồng quy:
♦ Cách 1: Sử dụng đường thẳng chứa hai điểm
- Bước 1: Chọn hai điểm trong ba điểm A, B, C (ví dụ A và B).
- Bước 2: Xác định đường thẳng d đi qua hai điểm A và B.
- Bước 3: Chứng minh rằng điểm thứ ba (C) cũng nằm trên đường thẳng d.
Nếu C ∈ d thì ba điểm A, B, C đồng quy trên đường thẳng d.
- Kết luận: Ba điểm A, B, C thẳng hàng.
♦ Cách 2: Sử dụng phương pháp hình học cơ bản
- Bước 1: Vẽ hai đoạn thẳng AB và BC.
- Bước 2: Chứng minh rằng hai đoạn thẳng AB và BC nối tiếp nhau trên một đường thẳng duy nhất (bằng các tính chất như góc bẹt, góc kề bù, hoặc các tỷ lệ đồng dạng).
- Kết luận: Hai đoạn thẳng nối liền trên cùng một đường thẳng chứng tỏ ba điểm thẳng hàng.
♦ Cách 3: Sử dụng các đối tượng đồng quy
- Bước 1: Chứng minh rằng các điểm A, B, C là giao điểm của các đường đặc biệt trong hình học (như đường trung trực, đường phân giác, hoặc đường cao).
- Bước 2: Xác định đường thẳng duy nhất chứa cả ba giao điểm này.
Ví dụ: Nếu ba điểm là giao điểm của ba đường trung trực, chúng sẽ nằm trên cùng một đường thẳng.
- Kết luận: Ba điểm thẳng hàng vì chúng đồng quy trên một đường thẳng duy nhất.
3. Sử dụng tiên đề Euclid
♦ Cách 1: Dùng tính chất đường trung trực
- Bước 1: Xác định ba điểm A, B, C.
- Bước 2: Chứng minh rằng cả ba điểm cùng cách đều hai đầu mút của một đoạn thẳng PQ nào đó.
Ví dụ: Nếu d(A,P) = d(A,Q), d(B,P)=d(B,Q) và d(C,P)=d(C,Q) thì cả ba điểm A, B, C cùng nằm trên đường trung trực của đoạn PQ.
- Bước 3: Kết luận rằng ba điểm A, B, C nằm trên đường trung trực, nên chúng thẳng hàng.
♦ Cách 2: Chứng minh bằng quan hệ song song
- Bước 1: Giả sử A, B, C là ba điểm trên một mặt phẳng.
- Bước 2: Chứng minh rằng có hai đường thẳng qua A và B, hoặc qua B và C, cùng song song với một đường thẳng thứ ba d.
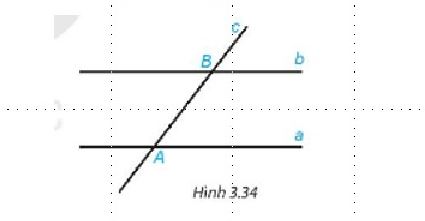
Nếu hai đường thẳng qua A, B và B, C đều song song với d thì A, B, C phải nằm trên cùng một đường thẳng (theo tiên đề Euclid).
II. Cách chứng minh ba điểm thẳng hàng lớp 8
1. Sử dụng định lý Thales:
🍀 Nguyên lý cơ bản của định lý Thales:
Khi xét ba điểm A, B, C, nếu tỷ lệ các đoạn thẳng bằng nhau AB/BC=AD/DC (nếu D là điểm bất kỳ trên một đường song song) thì ba điểm A, B, C thẳng hàng.
🍀 Phương pháp chứng minh ba điểm thẳng hàng bằng định lý Thales:
- Bước 1: Xác định ba điểm cần chứng minh
Xét ba điểm A, B, C trên mặt phẳng.
- Bước 2: Áp dụng định lý Thales
Giả sử có một đường thẳng song song với đoạn thẳng AC, gọi đường đó là d và trên d có điểm D.
Theo định lý Thales, nếu tỷ lệ AB/BC=AD/DC thì ba điểm A, B, C phải thẳng hàng.
- Bước 3: Kết luận
Nếu tỷ lệ trên đúng, ba điểm A, B, C nằm trên cùng một đường thẳng.
2. Phương pháp tọa độ:
🍀 Nguyên lý cơ bản:
Ba điểm A(x1,y1), B(x2,y2), C(x3,y3) thẳng hàng nếu và chỉ nếu:
(y2 – y1)/(x2 – x1) = (y3 – y2)/(x3 – x2)
Hoặc:
(y2 − y1)(x3 − x2) = (y3 − y2)(x2 − x1).
🍀 Phương pháp chứng minh ba điểm thẳng hàng bằng phương pháp tọa độ:
- Bước 1: Đặt tọa độ của ba điểm
Giả sử ba điểm là A(x1,y1), B(x2,y2), C(x3,y3)
- Bước 2: Tính hệ số góc giữa các cặp điểm
Tính hệ số góc của đoạn AB: mAB = (y2 − y1)/(x2 − x1).
Tính hệ số góc của đoạn BC: mBC = (y3 − y2)/(x3 − x2).
- Bước 3: So sánh hệ số góc
Nếu mAB = mBC tức là (y2 – y1)/(x2 – x1) = (y3 – y2)/(x3 – x2) thì ba điểm A, B, C thẳng hàng.
- Bước 4: Kiểm tra điều kiện đặc biệt
Nếu hai trong ba điểm có cùng tọa độ x (tức là đường thẳng song song với trục Oy), kiểm tra xem điểm thứ ba có cùng tọa độ x hay không. Nếu đúng thì ba điểm đó thẳng hàng.
3. Dựa trên tính chất đồng dạng:
🍀 Nguyên lý cơ bản:
- Khi hai tam giác đồng dạng, các cạnh tương ứng tỷ lệ với nhau.
- Sự đồng dạng của hai tam giác có thể dẫn đến các tính chất hình học đặc biệt như song song, góc bù, hoặc điểm đồng quy.
- Ba điểm thẳng hàng nếu một trong các mối quan hệ trên được sử dụng để kết nối các điểm.
Sử dụng tính chất đồng dạng để chứng minh ba điểm thẳng hàng dựa vào việc tận dụng mối quan hệ giữa các tam giác đồng dạng hoặc tỷ lệ các đoạn thẳng liên quan. Đây là một cách tiếp cận gián tiếp nhưng rất hiệu quả trong các bài toán hình học phẳng.
🍀 Phương pháp chứng minh ba điểm thẳng hàng bằng tính chất đồng dạng:
♦ Cách 1: Tận dụng định lý Thales mở rộng qua tam giác đồng dạng
- Bước 1: Xác định hai tam giác đồng dạng trong bài toán (thường có các đường chia đoạn hoặc song song).
- Bước 2: Sử dụng tính chất đồng dạng để chứng minh tỷ lệ các đoạn thẳng liên quan giữa ba điểm.
- Bước 3: Nếu tỷ lệ thoả mãn định lý Thales (hoặc định lý về tỷ lệ đoạn thẳng), ba điểm sẽ thẳng hàng.
♦ Cách 2: Chứng minh các đường song song dẫn đến thẳng hàng
- Bước 1: Sử dụng tính chất đồng dạng của tam giác để chứng minh rằng các đường thẳng qua ba điểm là song song với nhau hoặc tạo góc bù.
- Bước 2: Kết luận rằng ba điểm nằm trên cùng một đường thẳng dựa vào mối quan hệ góc hoặc tỷ lệ.
♦ Cách 3: Chia đoạn theo tỷ lệ đồng dạng
- Bước 1: Xác định tam giác đồng dạng có chứa ba điểm liên quan (ví dụ, ba điểm nằm trên đường chéo của hình thang).
- Bước 2: Sử dụng tính chất đồng dạng để chia các đoạn thẳng theo tỷ lệ.
- Bước 3: Chứng minh rằng các đoạn thẳng này thẳng hàng dựa trên định lý Thales.
III. Cách chứng minh ba điểm thẳng hàng lớp 9
1. Phương pháp vectơ:
🍀 Nguyên lý cơ bản:
Ba điểm A, B, C thẳng hàng khi vectơ AB và AC cùng phương, tức là vectơ AB = k. vectơ AC với k là số thực.
♦ Điều kiện cùng phương của hai vectơ:
- Hai vectơ u và v cùng phương nếu: vectơ u x vectơ v = 0
- Hoặc nếu vectơ này là một bội số của vectơ kia: vectơ u = k.vectơ v
🍀 Các bước chứng minh bằng phương pháp vectơ:
- Bước 1: Biểu diễn các vectơ
Cho ba điểm A(x1,y1), B(x2,y2), C(x3,y3).
Biểu diễn các vectơ AB và AC:
Vectơ AB = (x2−x1, y2−y1)
Vectơ AC =(x3 − x1, y3 − y1)
- Bước 2: Kiểm tra tính cùng phương
Kiểm tra điều kiện: vectơ AB x vectơ AC = 0.
Tích chéo giữa hai vectơ:
Vectơ AB x vectơ AC = (x2 − x1)(y3 − y1) − (y2 − y1)(x3 − x1)
Nếu biểu thức trên bằng 0 thì hai vectơ cùng phương và A,B,C thẳng hàng.
2. Sử dụng phương trình đường thẳng:
🍀 Nguyên lý cơ bản:
Ba điểm A(x1, y1), B(x2, y2), C(x3, y3) thẳng hàng nếu tọa độ của điểm C thỏa mãn phương trình đường thẳng đi qua hai điểm A và B.
Phương trình tổng quát của đường thẳng:
ax + by + c = 0 với a,b,c là các hằng số.
🍀 Các bước chứng minh ba điểm thẳng hàng bằng phương pháp sử dụng phương trình đường thẳng:
- Bước 1: Lập phương trình đường thẳng qua hai điểm A(x1, y1) và B(x2, y2)
Tính hệ số a và b dựa trên tọa độ: a = y2 − y1, b = x1 − x2.
Tìm hệ số c bằng cách thay tọa độ một trong hai điểm (ví dụ A(x1, y1) vào phương trình: c = −(ax1 + by1).
Phương trình đường thẳng trở thành: a(x − x1) + b(y − y1) = 0 hoặc ax + by + c = 0.
- Bước 2: Kiểm tra điểm thứ ba C(x3, y3)
Thay tọa độ C(x3, y3) vào phương trình đường thẳng: ax3 + by3 + c.
Nếu kết quả bằng 0 thì C nằm trên đường thẳng và ba điểm A,B,C thẳng hàng.
3. Dùng các định lý nâng cao (Menelaus hoặc Ceva):
🍀 Sử dụng định lý Menelaus
♦ Định lý Menelaus:
- Phát biểu:
Cho tam giác △ABC, một đường thẳng bất kỳ cắt các cạnh (hoặc phần kéo dài của các cạnh) BC, CA và AB tại các điểm D, E, F tương ứng. Ba điểm D,E,F thẳng hàng nếu và chỉ nếu:
BD/DC x CE/EA x AF/FB=1
- Ý nghĩa:
Nếu D, E, F nằm trên các đường kéo dài của các cạnh tam giác và thoả mãn tỷ lệ trên, thì chúng nằm trên cùng một đường thẳng (thẳng hàng).
♦ Phương pháp chứng minh ba điểm thẳng hàng bằng định lý Menelaus:
- Bước 1: Xác định tam giác và các điểm
Xác định tam giác △ABC.
Xác định ba điểm D, E, F nằm trên các cạnh hoặc đường kéo dài của tam giác.
- Bước 2: Tính các tỷ lệ
Tính các tỷ lệ của đoạn thẳng trên các cạnh: BD/DC, CE/EA, AF/FB.
- Bước 3: Kiểm tra điều kiện của định lý Menelaus
Tính tích: BD/DC x CE/EA x AF/FB
Nếu tích bằng 1 thì ba điểm D, E, F thẳng hàng.
🍀 Sử dụng định lý Ceva
♦ Phát biểu Định lý Ceva:
Cho tam giác △ABC, các đường thẳng qua các đỉnh A,B,C lần lượt cắt các cạnh đối diện BC, CA, AB tại các điểm D, E, F.
Ba đường thẳng AD, BE, CF đồng quy tại một điểm nếu và chỉ nếu:
BD/DC x CE/EA x AF/FB=1.
♦ Ứng dụng Định lý Ceva để chứng minh ba điểm thẳng hàng:
Định lý Ceva có thể được sử dụng gián tiếp để chứng minh ba điểm thẳng hàng bằng cách áp dụng định lý vào các đường thẳng nối ba điểm cần kiểm tra.
Kết nối với sự thẳng hàng:
Ba điểm D, E, F trên các cạnh BC, CA, AB của tam giác thẳng hàng (nằm trên cùng một đường thẳng) nếu ba đường thẳng AD, BE, CF đồng quy.
Điều này được kiểm tra bằng cách sử dụng điều kiện của định lý Ceva:
BD/DC x CE/EA x AF/FB=1.
♦ Các bước chứng minh ba điểm thẳng hàng bằng Định lý Ceva:
- Bước 1: Xác định tam giác và các điểm cần kiểm tra
Chọn tam giác △ABC.
Xác định ba điểm D, E, F trên các cạnh BC, CA, AB.
- Bước 2: Tính các tỷ lệ đoạn thẳng
Tính các tỷ lệ: BD/DC, CE/EA, AF/FB
- Bước 3: Áp dụng định lý Ceva
Tính tích của các tỷ lệ: BD/DC x CE/EA x AF/FB.
Nếu tích bằng 1, thì AD, BE, CF đồng quy và ba điểm D, E, F thẳng hàng.
♦ Lưu ý khi sử dụng Định lý Ceva:
- Chiều của các đoạn thẳng: Tính tỷ lệ các đoạn thẳng theo cùng một hướng để đảm bảo dấu chính xác.
- Sự đồng quy và sự thẳng hàng: Định lý Ceva kiểm tra đồng quy, nhưng trong trường hợp tam giác mở rộng, nó được sử dụng để kiểm tra sự thẳng hàng của các điểm.
Hi vọng các cách chứng minh 3 điểm thẳng hàng lớp 7, 8, 9 kèm file PDF để tải về miễn phí ở trên đã giúp các em thành thạo các cách chứng minh ba điểm thẳng hàng cũng như đạt điểm cao môn Toán trong các bài thi và bài kiểm tra.
Đừng quên tham khảo các đầu sách tham khảo lớp 7, lớp 8 và lớp 9 cực chất lượng của Tkbooks để học tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh THCS hàng đầu tại Việt Nam!


