Cách chứng minh 2 mặt phẳng vuông góc dựa vào định nghĩa, tính chất và góc nhị diện

Cách chứng minh 2 mặt phẳng vuông góc như thế nào? Dựa vào định nghĩa, tính chất, hay góc nhị diện?

Bài viết dưới đây sẽ giúp bạn hệ thống lại toàn bộ lý thuyết nền tảng, các điều kiện xác định mặt phẳng vuông góc, cũng như những phương pháp chứng minh hiệu quả kèm ví dụ minh họa thực tế.

Mời các bạn tham khảo!

I. Góc giữa 2 mặt phẳng và hai mặt phẳng vuông góc

• Cho hai mặt phẳng (P) và (Q). Lấy các đường thẳng a,b tương ứng vuông góc với (P), (Q). Khi đó, góc giữa a và b không phụ thuộc vào vị trí của a, b và được gọi là góc giữa hai mặt phẳng (P) và (Q).
• Hai mặt phẳng (P) và (Q) được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°.

Chú ý. Nếu α là góc giữa hai mặt phẳng (P) và (Q) thì 0°≤α ≤90°.

Nhận xét:

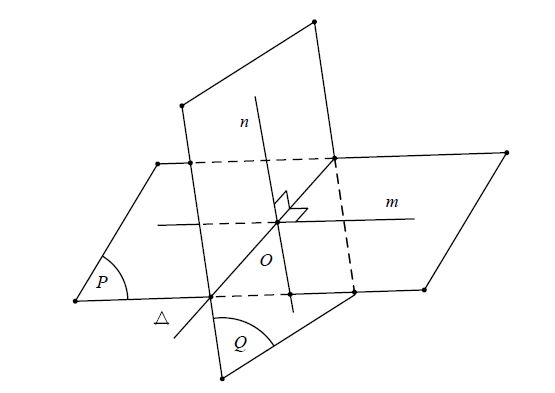
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến Δ. Lấy hai đường thẳng m, n tương ứng thuộc (P), (Q) và cùng vuông góc với Δ tại một điểm O (nói cách khác, lấy một mặt phẳng vuông góc với Δ, cắt (P), (Q) tương ứng theo các giao tuyến m, n). Khi đó, góc giữa (P) và (Q) bằng góc giữa m và n.

Đặc biệt: (P) vuông góc với (Q) khi và chỉ khi m vuông góc với n.

II. Điều kiện để hai mặt phẳng vuông góc

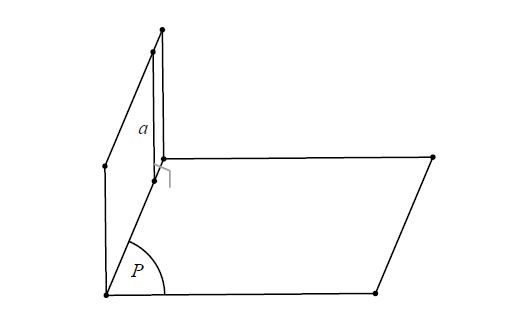
Định lý: Nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia thì hai mặt phẳng đó vuông góc với nhau.

III. Tính chất của 2 mặt phẳng vuông góc

Tính chất 1:

Cho hai mặt phẳng vuông góc, một đường thẳng bất kì nằm trong mặt phẳng này mà vuông góc với giao tuyến, cũng đều vuông góc với mặt phẳng kia.

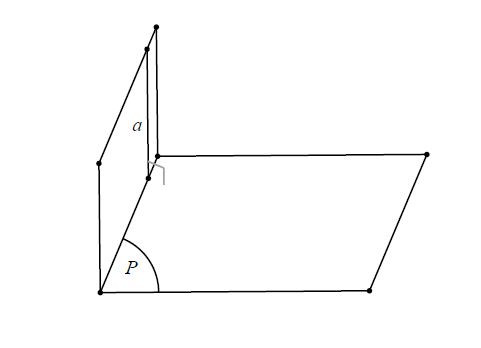
Nhận xét: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Mỗi đường thẳng qua điểm O thuộc (P) và vuông góc với mặt phẳng (Q) thì đường thẳng đó thuộc mặt phẳng (P).

Tính chất 2:

Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba, thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

Ví dụ. Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA⊥(ABCD). Gọi B’, C’, D’ tương ứng là hình chiếu của A trên SB, SC, SD. Chứng minh rằng:

a) (SBC)⊥(SAB), AB′⊥(SBC), AD′⊥(SCD).

b) Các điểm A, B, C, D cùng thuộc một mặt phẳng.

Lời giải:

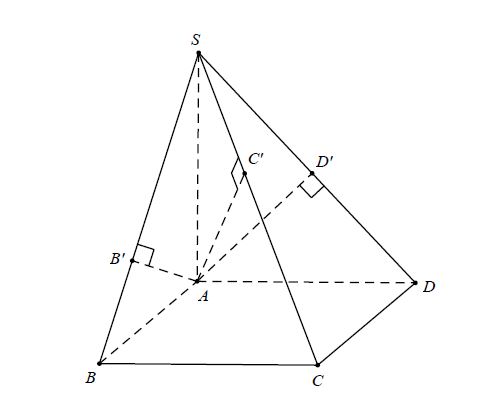
a) Vì BC⊥SA và BC⊥AB nên BC⊥(SAB). Do đó, (SBC)⊥(SAB). Đường thẳng AB’ thuộc (SAB) và vuông góc với SB nên AB⊥(SBC). Tương tự AD’⊥(SCD).

b) Từ câu a ta có AB’⊥SC, AD’⊥ Các đường thẳng AB, AC, AD cùng đi qua A và vuông góc với SC nên cùng thuộc một mặt phẳng. Do đó bốn điểm A, B, C, D cùng thuộc một mặt phẳng.

IV. Góc nhị diện

Hình gồm hai nửa mặt phẳng (P), (Q) có chung bờ a được gọi là một góc nhị diện, kí hiệu là [P, a, Q]. Đường thẳng a và các nữa mặt phẳng (P), (Q) tương ứng được gọi là cạnh và các mặt của góc nhị diện đó.

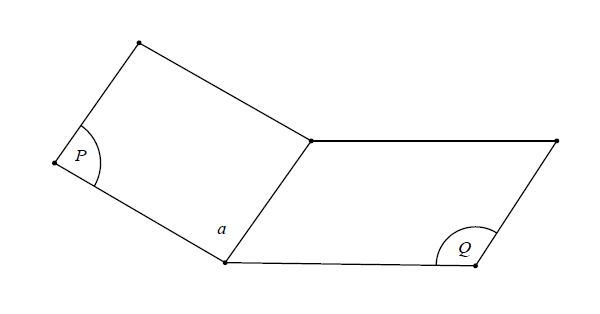
Mỗi đường thẳng a trong một mặt phẳng chia mặt phẳng thành hai phần, mỗi phần cùng với a là một nửa mặt phẳng bờ.

Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P, a, Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P, a, Q] (gọi tắt là góc phẳng nhị diện). Số đo của góc xOy không phụ thuộc vào vị trí của O trên a, được gọi là số đo của góc nhị diện [P, a, Q].

Mặt phẳng chứa góc phẳng nhị diện xOy của [P, a, Q] vuông góc với cạnh a.

Chú ý:

• Số đo của góc nhị diện có thể nhận giá trị từ 0° đến 180°. Góc nhị diện được gọi là vuông, nhọn, tù nếu nó có số đo tương ứng bằng, nhỏ hơn, lớn hơn 90°.
• Đối với hai điểm M,N không thuộc đường thẳng a, ta kí hiệu [M, a, N] là góc nhị diện có cạnh a và các mặt tương ứng chứa M, N.
• Hai mặt phẳng cắt nhau tạo thành bốn góc nhị diện. Nếu một trong bốn góc nhị diện đó là góc nhị diện vuông thì các góc nhị diện còn lại cũng là góc nhị diện vuông.

V. Cách chứng minh 2 mặt phẳng vuông góc

Cách 1: Dựa trên định nghĩa góc giữa hai mặt phẳng

• Nếu hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến Δ, ta thực hiện:
• Dựng mặt phẳng vuông góc với Δ tại điểm O bất kỳ.
• Mặt phẳng này cắt (P) và (Q) lần lượt theo hai đường thẳng m và n.
• Nếu m ⊥ n thì suy ra (P) ⊥ (Q).

▶ Cơ sở lý thuyết: Góc giữa hai mặt phẳng chính là góc giữa hai đường thẳng m, n cùng vuông góc với giao tuyến Δ.

❖ Ví dụ:

Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến Δ.

Dựng mặt phẳng (R) vuông góc với Δ tại điểm O bất kỳ. Mặt phẳng (R) cắt (P) theo đường thẳng m, cắt (Q) theo đường thẳng n, biết rằng m ⊥ n.

❖ Kết luận:

⇒ Góc giữa (P) và (Q) bằng góc giữa m và n ⇒ (P) ⊥ (Q).

🔹 Tình huống thực tế: Trong hình chóp tứ giác đều S.ABCD, mặt phẳng (SAC) và (SBD) cắt nhau theo đường chéo của hình vuông ABCD. Dựng mặt phẳng trung trực của cạnh chéo này → hai mặt phẳng bên tạo thành hai đường vuông góc giao nhau ⇒ mặt phẳng vuông góc.

Cách 2: Dựa trên định lý về mặt phẳng chứa đường vuông góc

Nếu mặt phẳng (P) chứa đường thẳng a và a ⊥ (Q), thì (P) ⊥ (Q).

▶ Ứng dụng: Trong bài toán hình học không gian, khi tìm được một đường trong (P) mà vuông góc hoàn toàn với (Q), ta khẳng định hai mặt phẳng vuông góc.

❖ Ví dụ:

Trong hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với mặt phẳng đáy (ABCD).

❖ Xét mặt phẳng (SAC):

Đường SA thuộc (SAC).

SA ⊥ (ABCD).

❖ Kết luận:

⇒ (SAC) ⊥ (ABCD) (theo định lý: mặt phẳng chứa đường thẳng vuông góc với mặt phẳng khác thì vuông góc với mặt phẳng đó).

Cách 3: Dựa trên tính chất hình học của hai mặt phẳng vuông góc

Nếu:

• (P) và (Q) cắt nhau theo giao tuyến Δ;
• Có một đường trong (P) vuông góc với Δ;
• Đường đó vuông góc với toàn mặt phẳng (Q).

⇒ Khi đó, suy ra (P) ⊥ (Q).

▶ Tính chất 1: Nếu một đường nằm trong một mặt phẳng và vuông góc với giao tuyến, lại vuông góc với mặt phẳng còn lại → hai mặt phẳng vuông góc.

❖ Ví dụ:

Trong hình chóp S.ABCD có đáy là hình chữ nhật và SA ⊥ (ABCD). Xét các mặt phẳng (SAB) và (SBC).

Giao tuyến của (SAB) và (SBC) là cạnh SB.

Trong (SAB), xét đường AB’ vuông góc với SB và AB’ ⊂ (SAB).

AB’ cũng vuông góc với (SBC).

❖ Kết luận:

⇒ (SAB) ⊥ (SBC).

Cách 4: Chứng minh dựa trên góc nhị diện

Hai mặt phẳng (P) và (Q) tạo thành góc nhị diện [P, a, Q].

Nếu một trong các góc phẳng nhị diện là 90°, thì các góc còn lại cũng là góc vuông.

▶ Kết luận: Nếu đo được góc phẳng nhị diện = 90°, có thể kết luận (P) ⊥ (Q).

❖ Ví dụ:

Trong hình hộp chữ nhật ABCD.A’B’C’D’, xét hai mặt phẳng (ABC) và (ABB’A’).

Giao tuyến: cạnh AB.

Lấy điểm O ∈ AB, dựng mặt phẳng vuông góc AB tại O.

Mặt phẳng này cắt hai mặt (ABC) và (ABB’A’) theo hai đường thẳng vuông góc nhau (m và n), tạo thành góc xOy = 90°.

❖ Kết luận:

⇒ Góc nhị diện giữa hai mặt bằng 90° ⇒ (ABC) ⊥ (ABB’A’).

Cách 5: Phương pháp dựng hình trong hình học không gian

Phương pháp 5.1: Dựng hình trong hình chóp có đường cao vuông góc đáy

• Bước 1: Tìm đường giao tuyến giữa mặt bên và mặt đáy (thường là cạnh).
• Bước 2: Từ chân đường cao hạ vuông góc đến giao tuyến.
• Bước 3: Nối từ đỉnh đến điểm vừa dựng → góc giữa hai mặt phẳng là góc tại đỉnh.

▶ Nếu góc tạo thành = 90°, hai mặt phẳng vuông góc.

❖ Ví dụ:

Cho hình chóp S.ABCD, đáy là hình chữ nhật, SA ⊥ (ABCD).

Yêu cầu: chứng minh (SCD) ⊥ (ABCD).

❖ Các bước:

Từ A hạ vuông góc đến cạnh CD tại M.

Nối SM → góc SMA là góc giữa hai mặt phẳng.

❖ Giả sử SMA = 90°, ta có:

⇒ (SCD) ⊥ (ABCD).

Phương pháp 5.2: Dựng hình trong hình chóp không có cạnh nào vuông góc đáy

• Bước 1: Hạ đường cao từ đỉnh xuống đáy.
• Bước 2: Hạ tiếp từ chân đường cao vuông góc đến giao tuyến của hai mặt.
• Bước 3: Nối lại để tạo thành tam giác vuông → kiểm tra góc tại đỉnh.

▶ Nếu góc tại đỉnh tam giác = 90°, thì các mặt phẳng vuông góc.

❖ Ví dụ:

Hình chóp S.ABCD, không có cạnh bên nào vuông góc với đáy.

Yêu cầu: chứng minh (SCD) ⊥ (ABCD).

❖ Các bước:

Hạ SH ⊥ (ABCD).

Từ H hạ vuông góc xuống CD tại điểm M.

Nối SM → góc SMH là góc giữa mặt bên và mặt đáy.

❖ Nếu SMH = 90° thì:

⇒ (SCD) ⊥ (ABCD).

Cách 6: Chứng minh bằng phương pháp tổng hợp

Tổng kết, có thể chứng minh 2 mặt phẳng vuông góc bằng các cách sau:

Phương pháp	Mô tả ngắn gọn	Điều kiện để (P) ⊥ (Q)
Dựng hai đường vuông góc giao tuyến	m ⊂ (P), n ⊂ (Q), m ⊥ n	m ⊥ n
Mặt phẳng chứa đường vuông góc	a ⊂ (P), a ⊥ (Q)	Có đường thẳng thuộc mặt này vuông góc mặt kia
Tính chất hình học	Đường vuông góc giao tuyến và vuông góc mặt còn lại	Thỏa mãn tính chất
Góc nhị diện	Đo góc phẳng nhị diện	Góc = 90°
Dựng hình hình học không gian	Dùng hình chiếu và tam giác	Góc tại đỉnh = 90°

VI. Bài tập chứng minh 2 mặt phẳng vuông góc

Bài 1. Cho hình chóp S.ABC có SA⊥(ABC). Gọi H là hình chiếu của A trên BC.

a) Chứng minh rằng (SAB)⊥(ABC) và (SAH)⊥(SBC).

b) Giả sử tam giác ABC vuông tại A, ABC = 30°, AC = a, SA = (a√3)/2. Tính số đo của góc nhị diện [S, BC, A].

Bài 2. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a.

a) Tính độ dài đường chéo của hình lập phương.

b) Chứng minh rằng (ACC’A’)⊥(BDD’B’).

c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng COC’ là một góc phẳng của góc nhị diện [C, BD, C]. Tính (gần đúng) số đo của các góc nhị diện [C, BD, C], [A, BD, C’].

Bài 3. Cho hình hộp chữ nhật ABCD.A’B’C’D’.

a) Chứng minh rằng (BDD’B’)⊥(ABCD)

b) Xác định hình chiếu của AC’ trên mặt phẳng (ABCD).

c) Cho AB = a, BC = b, CC’ = c. Tính AC.

Bài 4. Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b.

a) Tinh sin của góc tạo bởi cạnh bên và mặt đáy.

b) Tính tang của góc giữa mặt phẳng chứa mặt đáy và mặt phẳng chứa mặt bên.

Bài 5. Hai mái nhà trong hình dưới đây là hai hình chữ nhật. Giả sử AB= 4,8m; OA 2,8 m; OB 4m.

a) Tính (gần đúng) số đo của góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chứa hai mái nhà.

b) Chứng minh rằng mặt phẳng (OAB) vuông góc với mặt đất phẳng. Lưu ý: Đường giao giữa hai mái (đường nóc) song song với mặt đất.

c) Điểm A ở độ cao (so với mặt đất) hơn điểm B là 0,5 m. Tinh (gần đúng ) góc giữa mái nhà (chứa OB) so với mặt đất.

Bài 6. Độ dốc của mái nhà, mặt sân, con đường thẳng là tang của góc tạo bởi mái nhà mặt sân, con đường thẳng đó với mặt phẳng nằm ngang. Độ dốc của đường thẳng dành cho người khuyết tật được quy định là không quá 1/12. Hỏi theo đó, góc tạo bởi đường dành cho người khuyết tật và mặt phẳng nằm ngang không vượt quá bao nhiêu độ? (Làm tròn kết quả đến chữ số thập phân thứ hai).

📘 Bạn muốn học Toán hiệu quả hơn, hệ thống kiến thức gọn gàng và dễ tra cứu?

Đừng bỏ lỡ cuốn Sổ tay Toán Học cấp 3 – All in one của TKBooks – trợ thủ đắc lực dành cho học sinh THPT trong mọi kỳ thi!

Cuốn sách tổng hợp đầy đủ các công thức, định lý, phương pháp giải nhanh của ba lớp 10, 11, 12 – được trình bày logic, khoa học và cực kỳ dễ tra cứu. Dù bạn đang học đại số, hình học không gian hay ôn luyện thi tốt nghiệp THPT, cuốn sổ tay này sẽ giúp bạn tiết kiệm thời gian và học đúng trọng tâm.

👉 Đọc thử ngay tại đây hoặc Đặt mua bản in chính hãng tại Tkbooks để có trong tay một công cụ học tập toàn diện, nhỏ gọn và hiệu quả.

Tkbooks.vn