Chưa có sản phẩm trong giỏ hàng.
Các dạng toán tập hợp lớp 6 cơ bản và nâng cao kèm file PDF miễn phí
Các dạng toán tập hợp lớp 6 cơ bản và nâng cao là một trong những chủ đề quan trọng và thú vị trong chương trình Toán lớp 6.
Để giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán tập hợp, bài viết này sẽ giới thiệu các dạng toán cơ bản và nâng cao về tập hợp.
Không chỉ vậy, các em còn có thể tải miễn phí file PDF chứa các bài tập phong phú và đa dạng, được biên soạn kỹ lưỡng nhằm đáp ứng nhu cầu học tập và ôn luyện.
Mời các em tham khảo!
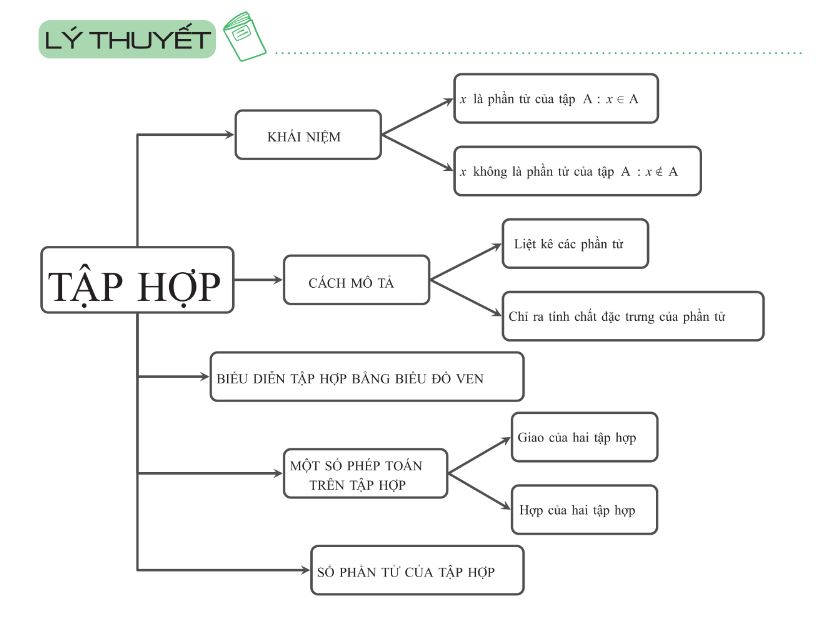
I. Kiến thức về tập hợp lớp 6
1. Khái niệm tập hợp
Tập hợp là một khái niệm thường gặp khi học về toán, tuy nhiên khái niệm này được hiểu một cách hình thức để biểu thị về các đối tượng có chung một đặc tính nào đó.
Ví dụ:
Ví dụ 1. Tập hợp tất cả học sinh trong lớp 9A.
Ví dụ 2. Tập hợp số sách trên giá sách.
Ví dụ 3. Tập hợp số bút trên mặt bàn.
Người ta thường dùng các chữ cái in hoa A, B, C, … để kí hiệu tập hợp.
Kí hiệu x ∈ A (x thuộc A) có nghĩa “ x là một phần tử của tập A”.
Kí hiệu y ∉ A (y không thuộc A) có nghĩa “ y không là phần tử của tập A”.
2. Cách viết và ký hiệu một tập hợp
Một tập hợp người ta thường ký hiệu nó bằng chữ cái in hoa như: A; B… và thường được viết kiểu như sau
Ví dụ 1: Tập hợp A ={a; b; c; d}
Trong đó A được gọi là tập hợp, a;b;c; d được gọi là các phần tử của tập hợp A.
Một tập hợp có thể có: 0 phần tử, 1 phần tử, nhiều phần tử, hoặc vô hạn phần tử.
Có hai cách viết tập hợp thường gặp là: liệt kê các phần tử của tập hợp, hoặc viết theo tính chất đặc trưng của các phần tử trong tập hợp.
Ví dụ 2: Viết theo kiểu lệt kê các phần tử B = {1;2;a;b;e}
Ví dụ 3: Viết kiểu đưa ra tính chất đặc trưng
A = {a | a = 2k; k ∈ N}. Đây là tập hợp A gồm các số tự nhiên chẵn.
Nếu tất cả các phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là tập con của B, và ký hiệu là A ⊂ B .
Tập hợp C gồm các phần tử thuộc cả tập hợp A và B được gọi là giao của A và B; ký hiệu là C = A ∩ B.
II. Các dạng toán tập hợp lớp 6
1. Dạng 1: Mô tả một tập hợp
a. Phương pháp
Dùng một chữ cái in hoa và dấu ngoặc nhọn, ta có thể mô tả một tập hợp theo hai cách:
- Liệt kê các phần tử của nó.
- Chỉ ra tính chất đặc trưng cho các phần tử của nó.
b. Các ví dụ
Ví dụ 1:
Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của tập hợp đó
a) Tập hợp A các chữ cái xuất hiện trong từ “KHAI GIẢNG”.
b) Tập hợp B các số tự nhiên nhỏ hơn 5.
Hướng dẫn giải
a) Các chữ cái xuất hiện trong từ “KHAI GIẢNG” là K; H; A; I; G; N.
Vậy A = {K; H; A; I; G; N} .
b) Các số tự nhiên nhỏ hơn 5 là 0; 1; 2, 3, 4.
Vậy B = {0; 1; 2; 3; 4}.
Ví dụ 2:
Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của tập hợp đó
a) C = {x | x là số tự nhiên chẵn, x < 10.
b) D = {x | x là số tự nhiên, 20 < x < 40, x : 5}.
Hướng dẫn giải
a) Các số tự nhiên chẵn x sao cho x < 10 là 0; 2; 4; 6; 8.
Vậy C = {0; 2; 4; 6; 8} .
b) Các số tự nhiên x sao cho 20 < x < 40 và x chia hết cho 5 là 25; 30; 35.
Vậy D = {25; 30; 35}.
Ví dụ 3:
Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
a) E = {1; 3; 5; 7; 9}.
b) F = {1; 4; 7; 10; 13; 16; 19).
Hướng dẫn giải
a) E = {x | x là số tự nhiên lẻ, x < 10}.
b) F = {x | x là số tự nhiên chia cho 3 dư 1, x < 20}.
2. Dạng 2: Sử dụng kí hiệu “∈”, “∉”
a. Phương pháp
Kí hiệu ∈ đọc là “là phần tử của” hoặc “thuộc”.
Kí hiệu ∉ đọc là “không phải là phần tử của” hoặc “không thuộc”.
Phần tử x thuộc tập hợp 4, kí hiệu là x∈A.
Phần tử x không thuộc tập hợp A, kí hiệu là x ∉ A.
b. Các ví dụ
Ví dụ 1:
Cho tập hợp A = {4; 6; 8; 10; 12} . Điền kí hiệu thích hợp vào chỗ ba chấm:
a) 12… A;
b) 2… A.
Hướng dẫn giải
Vì 12 là một phần tử của tập hợp A nên 12 ∈ A.
Vì 2 không là một phần tử của tập hợp A nên 2 ∉ A.
Ví dụ 2:
Cho tập hợp B = {x | x là số tự nhiên, x < 10}.
Các phần tử 0; 1; 5; 10; 13 có thuộc tập hợp B không? Viết câu trả lời bằng cách sử dụng ký hiệu ∈; ∉.
Hướng dẫn giải
Ta có B = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Các phần tử 0; 1; 5 thuộc tập hợp B . Ta viết 0 ∈ B; l ∈ B; 5 ∈ B.
Các phần tử 10; 13 không thuộc tập hợp B . Ta viết 10 ∉ B; 13 ∉ B.
Ví dụ 3:
Cho hai tập hợp E = {a;b}, F = {b;x;y}. Điền kí hiệu thích hợp vào chỗ ba chấm:
a) x…E;
b) y… F;
c) b… E;
d) b… F.
Hướng dẫn giải
a) Phần tử x không thuộc tập hợp E nên x ∉
Phần tử y thuộc tập hợp F nên y ∈ F.
Phần tử b thuộc tập hợp E nên b ∈ E .
Phần tử b thuộc tập hợp F nên b ∈ F .
3. Dạng 3: Minh họa một tập hợp cho trước bằng hình vẽ
a. Phương pháp
Sử dụng biểu đồ Ven. Đó là một đường cong khép kín, mỗi phần tử của tập hợp được biểu diễn bởi một điểm ở bên trong đường cong đó.
b. Các ví dụ
Ví dụ 1:
Nhìn vào hình dưới đây, hãy viết tập hợp A.
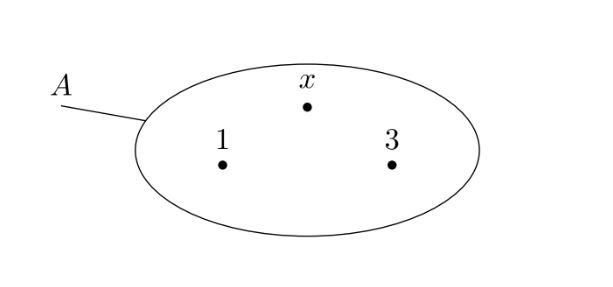
Hướng dẫn giải
Các phần tử 1; 3; x nằm trong đường cong khép kín nên chúng là các phần tử của tập hợp A. Vậy A ={1; 3; x}.
Ví dụ 2:
Gọi A là tập hợp các số tự nhiên chẵn x sao cho x nhỏ hơn 3. Hãy minh họa tập hợp A bằng sơ đồ Ven.
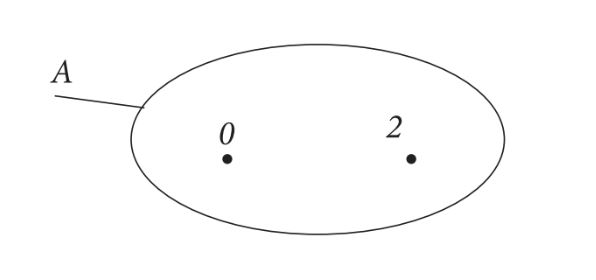
Hướng dẫn giải
Các số tự nhiên chẵn x mà x nhỏ hơn 3 là 0; 2. Nên A ={0; 2}
Ta có sơ đồ minh họa như hình dưới đây:
Ví dụ 3:
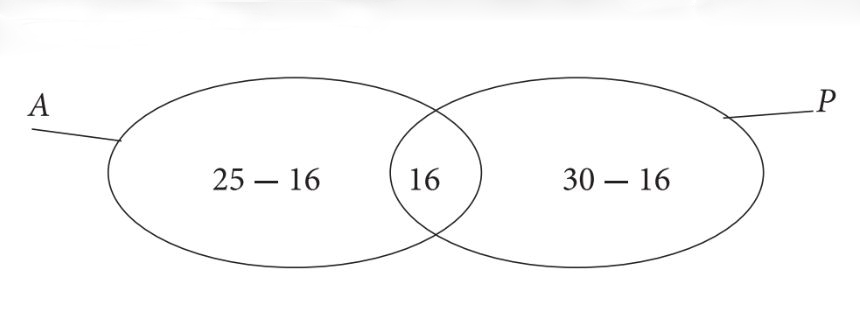
Trong một lớp học, mỗi học sinh đều đăng ký học tiếng Anh hoặc tiếng Pháp. Có 25 học sinh đăng ký học tiếng Anh, 30 học sinh đăng ký học tiếng Pháp, còn 16 học sinh đăng ký học cả hai thứ tiếng. Hỏi lớp học đó có bao nhiêu học sinh?
Hướng dẫn giải
Biểu diễn các học sinh đăng ký học tiếng Anh và tiếng Pháp như hình vẽ dưới. Có 16 học sinh đăng ký học cả hai thứ tiếng nằm ở phần hình chung của tiếng Anh và Pháp.
Số học sinh chỉ đăng ký học Tiếng Anh là: 25 – 16 = 9 (học sinh).
Số học sinh chỉ đăng ký học Tiếng Pháp là: 30 – 16 = 14 (học sinh).
Dựa vào hình vẽ ta có số học sinh của lớp là: 9 + 14 + 16 = 39 (học sinh).
III. Bài tập tổ hợp lớp 6 cơ bản và nâng cao tự luyện
1. Bằng cách liệt kê các phần tử, hãy viết tập hợp S các chữ cái trong từ “CÓ CHÍ THÌ NÊN”.
2. Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của tập hợp đó:
a) A = {x | x là số tự nhiên lẻ, 90 < x <101}.
b) B = {x | x là số tự nhiên, x + 13 = 13}.
c) C = {x | x là số tự nhiên, 0 : x = 0}.
3. Cho tập hợp Q = {2; 3; 5; 7} và H ={0; 1; m; n} . Chọn ký hiệu “∈”, “∉” thích hợp vào chỗ chấm.
a) 0 … Q
b) 7 … Q
c) 5 … H
d) m … H
4.
a) Viết tập hợp A các số tự nhiên x mà 8 + x = 20.
b) Viết tập hợp B các số tự nhiên x mà x + 3 < 5.
c) Viết tập hợp C các số tự nhiên x mà x + 0 = x.
d) Viết tập hợp D các số tự nhiên x mà 0 < 25 – x ≤ 7.
5. Cho tập hợp P = {0; 1; 4; 9; 16; 25; 36; 49; 64}. Hãy mô tả tập hợp P bằng cách nêu dấu hiệu đặc trưng các phần tử của nó.
6. Viết tập hợp D các số tự nhiên có hai chữ số mà chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 đơn vị.
7. Cho tập hợp A = {ab ∈ N | a + b = 5; a, b ∈ N}. Hãy viết tập hợp A dưới dạng liệt kê các phần tử của tập hợp A.
8. Cho tập hợp A gồm các số có hai chữ số mà tổng bằng 8, B là tập hợp các số có hai chữ số được tạo thành từ hai trong bốn số: 0; 3; 5; 8. Viết tập hợp A và B dưới dạng liệt kê các phần tử theo thứ tự tăng dần.
9. Tổng kết đợt thi đua chào mừng ngày 20 tháng 11 lớp 6A1 có 43 bạn được 1 điểm 10 trở lên, 40 bạn được từ 2 điểm 10 trở lên, 15 bạn được từ 3 điểm 10 trở lên, 5 bạn được 4 điểm 10. Biết không có ai được trên 4 điểm 10 hỏi trong đợt thi đua đó lớp 6A1 có bao nhiêu điểm 10?
Thông qua bài viết này, hy vọng rằng các em đã nắm vững các dạng toán tập hợp cơ bản và nâng cao. Chúc các em học tốt và đạt được nhiều thành tích cao trong học tập!
Các dạng toán tập hợp lớp 6 cơ bản và nâng cao ở trên đều có sẵn trong cuốn Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 6 – Tập 1. Quý phụ huynh và các em hãy nhanh tay sở hữu sách để hỗ trợ việc học cũng như đạt điểm số cao hơn trong môn Toán nhé!
Link đọc thử sách: https://drive.google.com/file/d/13IPKp8aPW5k9BTu1_jntilQfbZJoJB4X/view
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 6 hàng đầu tại Việt Nam!