Chưa có sản phẩm trong giỏ hàng.
Các dạng toán chuyển động lớp 5 cơ bản và nâng cao kèm đáp án
Các dạng toán chuyển động lớp 5 cơ bản và nâng cao kèm đáp án dưới đây sẽ là tài liệu hữu ích giúp các em ôn tập kiến thức cũng như nhận biết các dạng toán liên quan đến chuyển động, từ đó biết cách giải và đạt điểm cao hơn trong các bài thi, bài kiểm tra trên lớp.
Mời các em tham khảo!
I. Hướng dẫn làm các bài toán chuyển động lớp 5
1. Mối quan hệ giữa quãng đường (s), vận tốc (z) và thời gian (t)

📌 Trên cùng một quãng đường thì vận tốc và thời gian là 2 đại lượng tỉ lệ nghịch với nhau.
📌 Với cùng một vận tốc thì quãng đường và thời gian là 2 đại lượng tỉ lệ thuận với nhau.
📌 Với cùng một thời gian thì quãng đường và vận tốc là 2 đại lượng tỉ lệ thuận với nhau.
2. Một số dạng chuyển động đặc biệt
🏃 Chuyển động ngược chiều
Bài toán: Xe thứ nhất xuất phát từ A với vận tốc là a (đơn vị đo vận tốc, giả sử km/giờ) để đến B. Cùng lúc đó xe thứ hai xuất phát từ B với vận tốc là b (km/giờ) để đến A. Hỏi sau bao lâu hai xe gặp nhau?
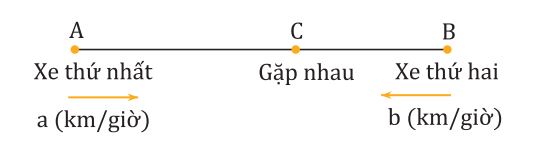
- Bước 1: Xác định được khoảng cách của hai xe là AB.
- Bước 2: Ta tính sau mỗi giờ cả hai xe đi được số ki-lô-mét là: a + b (km).
- Bước 3: Hai xe gặp nhau sau thời gian là: AB : (a + b) (giờ).
Công thức tổng quát:
Thời gian hai xe đi để gặp nhau = Khoảng cách hai xe : Tổng vận tốc |
🏃 Chuyển động cùng chiều
Bài toán: Xe thứ nhất xuất phát từ A với vận tốc là a (đơn vị đo vận tốc, giả sử km/giờ). Cùng lúc đó xe thứ hai xuất phát từ B với vận tốc là b (km/giờ) và đi cùng chiều đuổi theo xe thứ nhất (xem hình vẽ). Biết b > a. Hỏi xe thứ hai đuổi kịp xe thứ nhất sau bao lâu?
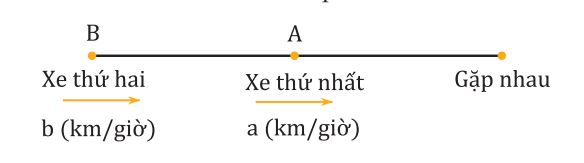
- Bước 1: Xác định được khoảng cách lúc đầu của hai xe là AB.
- Bước 2: Ta tính sau mỗi giờ xe thứ hai gần xe thứ nhất số ki-lô-mét là: b – a (km).
- Bước 3: Xe thứ hai đuổi kịp xe thứ nhất sau thời gian là: AB : (b – a) (giờ).
Công thức tổng quát:
| Thời gian hai xe đi để gặp nhau = Khoảng cách hai xe : Hiệu vận tốc |
II. Các dạng toán chuyển động lớp 5
1. Dạng cơ bản
Các bài toán chuyển động lớp 5 ở dạng cơ bản chủ yếu là các bài toán với các yêu cầu đơn giản, không có nhiều yếu tố phức tạp và cần tính toán trực tiếp.
a) Bài toán Chuyển động đều
Bài toán 1: Tính quãng đường đi được khi biết thời gian và vận tốc.
Ví dụ: Một chiếc xe chạy với vận tốc 50 km/h trong 3 giờ. Tính quãng đường xe đi được.
Hướng dẫn giải:
Áp dụng công thức tính quãng đường:
s = v x t = 50 × 3 = 150km
Đáp số: 150km.
Bài toán 2: Tính thời gian khi biết vận tốc và quãng đường.
Ví dụ: Một người đi bộ với tốc độ 4 km/h, đã đi được 12 km. Tính thời gian đi bộ.
Hướng dẫn giải:
Áp dụng công thức tính thời gian:
t = s : v = 12 : 4 = 3 giờ.
Đáp số: 3 giờ.
Bài toán 3: Tính vận tốc khi biết quãng đường và thời gian.
Ví dụ: Một chiếc ô tô đi quãng đường 100 km trong 2 giờ. Tính vận tốc của chiếc ô tô.
Áp dụng công thức tính vận tốc:
v = s : t = 100 : 2 = 50km/h
Đáp số: 50km/h.
b) Bài toán Chuyển động ngược chiều
Bài toán chuyển động ngược chiều thường yêu cầu các em tính tổng thời gian khi hai người cùng xuất phát từ hai nơi cách nhau một quãng đường, đi về phía nhau với các vận tốc khác nhau.
Ví dụ: Hai người xuất phát từ hai điểm A và B, cách nhau 60 km. Người thứ nhất đi với tốc độ 20 km/h, người thứ hai đi với tốc độ 30 km/h. Tính thời gian hai người gặp nhau.
Hướng dẫn giải:
Hai người xuất phát từ hai điểm A và B, cách nhau 60 km. Người thứ nhất đi với tốc độ 20 km/h, người thứ hai đi với tốc độ 30 km/h. Khi hai người đi về phía nhau, tổng vận tốc của họ sẽ là tổng của vận tốc của mỗi người.
Vậy tổng vận tốc v tổng của hai người là:
v tổng = v1 + v2 = 2- + 30 = 50km/h
Để tính thời gian hai người gặp nhau, chúng ta dùng công thức:
T = s : v tổng = 60 : 50 = 1,2 giờ.
Đáp số: 1,2 giờ hay 1 giờ 12 phút.
c) Bài toán chuyển động cùng chiều
Bài toán chuyển động cùng chiều thường yêu cầu các em tính thời gian gặp nhau khi hai người đi cùng chiều nhưng có vận tốc khác nhau.
Ví dụ: Hai người đi xe đạp từ A đến B. Người thứ nhất đi với tốc độ 10 km/h, người thứ hai đi với tốc độ 15 km/h. Hỏi sau bao lâu người thứ hai sẽ vượt được người thứ nhất nếu khoảng cách giữa hai người là 20 km.
Hướng dẫn giải:
Khi người thứ hai vượt người thứ nhất, ta cần tính sự chênh lệch vận tốc của hai người. Vì người thứ hai đi nhanh hơn, nên sự chênh lệch vận tốc là:
Δv = v2 − v1 = 15 − 10 = 5 km/h
Khi người thứ hai bắt đầu vượt người thứ nhất, khoảng cách giữa họ là 20 km. Thời gian để người thứ hai vượt người thứ nhất chính là thời gian mà người thứ hai đi hết quãng đường 20 km với vận tốc chênh lệch 5 km/h.
Áp dụng công thức thời gian:
t = s : Δv = 20 : 5 = 4 giờ.
Vậy sau 4 giờ, người thứ hai sẽ vượt người thứ nhất.
2. Dạng nâng cao
Dạng nâng cao có thể có nhiều yếu tố kết hợp hoặc yêu cầu người học phải áp dụng nhiều bước tính toán, tư duy logic để giải quyết.
a) Bài toán Chuyển động của nhiều đối tượng
Bài toán 1: Tính quãng đường khi có sự kết hợp giữa nhiều đối tượng chuyển động cùng chiều và ngược chiều.
Ví dụ: Một người đi bộ từ A đến B với vận tốc 4 km/h, trong khi một người khác đi từ B về A với vận tốc 6 km/h. Tính quãng đường giữa A và B nếu họ gặp nhau sau 1 giờ.
Hướng dẫn giải:
Khi hai người đi về phía nhau, tổng vận tốc của họ sẽ là tổng của vận tốc của từng người.
Vậy tổng vận tốc của hai người là:
v tổng = 4 + 6 = 10 km/h
Công thức tính quãng đường là:
s = v tổng x t = 10 x 1 = 10km.
Vậy quãng đường AB là 10km.
Bài toán 2: Bài toán chuyển động của nhiều đối tượng có sự thay đổi tốc độ giữa chừng.
Ví dụ: Một người xuất phát từ A với tốc độ 10 km/h, nhưng sau 1 giờ thì người đó tăng tốc lên 15 km/h. Hỏi sau bao lâu người đó sẽ đến B nếu khoảng cách từ A đến B là 50 km?
Hướng dẫn giải:
Trong 1 giờ đầu, người đó đi với tốc độ 10 km/h. Quãng đường đi được trong 1 giờ là:
s1 = v1 x t1 = 10 x 1 = 10 km
Sau 1 giờ, người đó đã đi được 10 km, nên quãng đường còn lại từ A đến B là:
s2 = 50 – 10 = 40 km
Sau 1 giờ, người đó tăng tốc lên 15 km/h. Để tính thời gian đi quãng đường còn lại 40 km, ta sử dụng công thức:
t2 = s2 : v2 = 40 : 15 = 8/3 giờ
Tổng thời gian người đó đi từ A đến B là tổng thời gian của hai phần:
Thời gian đi trong 1 giờ đầu: 1 giờ,
Thời gian đi quãng đường còn lại: 8/3 giờ
Tổng thời gian là:
t tổng = 1 + 8/3 = 3/3 + 8/3 = 11/3 giờ = 3 giờ 40 phút
Vậy người đó sẽ đến B sau 3 giờ 40 phút.
b) Bài toán Chuyển động có yếu tố thời gian và quãng đường thay đổi
Bài toán 1: Một người đi từ A đến B, quãng đường 80 km. Người đó đi với tốc độ 20 km/h trong 2 giờ đầu, rồi giảm tốc độ còn 10 km/h trong 1 giờ tiếp theo. Tính thời gian người đó đi hết quãng đường.
Hướng dẫn giải:
Trong 2 giờ đầu, người đó đi với tốc độ 20 km/h. Quãng đường đi được trong 2 giờ đầu là:
s1 = v1 x t1 = 20 x 2 = 40 km
Vậy sau 2 giờ, người đó đã đi được 40 km, và quãng đường còn lại để đi là:
s2 = 80 – 40 = 40 km
Sau 2 giờ đầu, người đó giảm tốc độ xuống còn 10 km/h và đi tiếp trong 1 giờ nữa. Quãng đường đi được trong 1 giờ với tốc độ 10 km/h là:
s2 = v2 x t2 = 10 x 1 = 10 km
Vậy, sau 3 giờ (2 giờ đầu và 1 giờ tiếp theo), người đó đã đi được 40 km + 10 km = 50 km. Quãng đường còn lại để đi là:
s3 = 80 – 50 = 30 km
Người đó tiếp tục đi với tốc độ 10 km/h. Thời gian để đi hết quãng đường còn lại 30 km là:
t3 = s3 : v2 = 30 : 10 = 3 giờ
Tổng thời gian người đó đi hết quãng đường là tổng thời gian của ba phần:
Thời gian đi 40 km với tốc độ 20 km/h: 2 giờ,
Thời gian đi 10 km với tốc độ 10 km/h: 1 giờ,
Thời gian đi 30 km với tốc độ 10 km/h: 3 giờ.
Vậy tổng thời gian là:
t tổng = 2 + 1 + 3 = 6 giờ
Vậy người đó sẽ đi hết quãng đường 80 km trong 6 giờ.
Bài toán 2: Một ô tô chạy với vận tốc 60 km/h trong 2 giờ đầu, rồi tăng tốc lên 80 km/h trong 3 giờ tiếp theo. Hỏi quãng đường ô tô đã đi trong tổng thời gian 5 giờ.
Hướng dẫn giải:
Trong 2 giờ đầu, ô tô chạy với vận tốc 60 km/h. Quãng đường đi được trong 2 giờ này là:
s1 = v1 x t1 = 60 x 2 = 120 km
Trong 3 giờ tiếp theo, ô tô tăng tốc lên 80 km/h. Quãng đường đi được trong 3 giờ này là:
s2 = v2 x t2 = 80 x 3 = 240 km
Tổng quãng đường ô tô đã đi trong 5 giờ là tổng của hai phần quãng đường đã tính:
s tổng = s1 + s2 = 120 + 240 = 360 km
Vậy quãng đường ô tô đã đi trong tổng thời gian 5 giờ là 360 km.
c) Bài toán liên quan đến Chuyển động trong các bài toán có tốc độ thay đổi liên tục
Các bài toán dạng này có chuyển động theo đoạn và yêu cầu tính tổng quãng đường.
Ví dụ: Một người đi từ A đến B, quãng đường là 100 km. Người đó đi với tốc độ 50 km/h trong 1 giờ đầu, rồi giảm tốc độ xuống còn 40 km/h trong 2 giờ tiếp theo. Hỏi người đó đi hết quãng đường trong bao lâu.
Hướng dẫn giải:
Trong 1 giờ đầu, người đó đi với tốc độ 50 km/h. Quãng đường đi được trong 1 giờ là:
s1 = v1 x t1 = 50 x 1 = 50 km
Sau 1 giờ, người đó đã đi được 50 km, và quãng đường còn lại là:
s còn lại = 100 – 50 = 50 km
Sau 1 giờ đầu, người đó giảm tốc độ xuống còn 40 km/h và đi tiếp trong 2 giờ nữa. Quãng đường đi được trong 2 giờ này là:
s2 = v2 x t2 = 40 x 2 = 80 km
Tuy nhiên, vì quãng đường còn lại chỉ có 50 km, nên người đó chỉ cần 1,25 giờ để đi hết quãng đường 50km còn lại.
t2 = 50 : 40 = 1,25 giờ
Tổng thời gian người đó đi hết quãng đường 100 km là:
t tổng = t1 + t2 = 1 + 1,25 = 2,25 giờ
Đáp số: 2,25 giờ.
III. Các bài tập vận dụng
Bài 1. Một ô tô đi từ A đến B trong một thời gian dự định. Nếu đi với vận tốc 45 km/giờ thì đến B chậm 30 phút so với dự định. Nếu đi với vận tốc 60 km/giờ thì lại đến B sớm 30 phút. Hỏi nếu đi với vận tốc 50 km/giờ thì ô tô đó đi hết quãng đường AB sau bao lâu?
Bài 2. Ba xe ô tô cùng đi một lúc từ A đến B, vận tốc ô tô thứ nhất là 30 km/giờ, vận tốc ô tô thứ hai là 45 km/giờ. Ô tô thứ ba đến sớm hơn ô tô thứ nhất 30 phút và chậm hơn ô tô thứ hai 40 phút. Tính độ dài quãng đường AB và vận tốc ô tô thứ ba.
Bài 3. Trong một cuộc thi chạy 10km, An đến đích trước Bình 2km và đến trước Cường 4km. Nếu vận tốc của mỗi người giữ nguyên thì Bình sẽ về đích trước Cường bao nhiêu ki-lô-mét?
Bài 4. Một ô tô đi từ A đến C gồm đoạn đường bằng AB và đoạn đường dốc BC, sau đó từ C lại quay về A mất tất cả 7 giờ. Biết vận tốc trên đoạn đường bằng là 40 km/giờ, xuống dốc là 60 km/giờ, lên dốc là 20 km/giờ và quãng đường AB bằng quãng đường BC. Tính độ dài quãng đường AC.
Bài 5. Trên quãng đường AB có 2 người đi xe đạp cùng khởi hành từ A để đến B. Người thứ nhất đi với vận tốc 10 km/giờ, người thứ hai đi với vận tốc 8 km/giờ. Sau khi đi 2 giờ, người thứ hai tăng vận tốc lên 14 km/giờ nên đuổi kịp người thứ nhất ở địa điểm C. Tính thời gian người thứ hai đã đi trên quãng đường AC và tính độ dài quãng đường AB, biết người thứ hai đi từ C đến B mất 2 giờ.
Bài 6. Một ô tô đi từ A đến B với vận tốc dự định và trong một thời gian dự định. Sau khi đi được một giờ thì ô tô giảm vận tốc chỉ còn bằng 80% vận tốc ban đầu nên đến B chậm 1 giờ so với dự định. Nếu từ A sau khi đi được 1 giờ, ô tô lại đi thêm 80km nữa mới giảm vận tốc còn bằng 80% so với vận tốc ban đầu thì ô tô đến B chỉ chậm 36 phút so với thời gian dự định. Tính độ dài quãng đường AB.
Bài 7. Rùa và Thỏ chạy thi trên một con đường thẳng. Vì 1 bước của Thỏ bằng 8 bước của Rùa nên Thỏ tin rằng mình sẽ thắng. Thỏ cho Rùa chạy trước. Khi Rùa chạy được 17 bước của Thỏ và chỉ còn cách đích 80 bước của Rùa thì Thỏ bắt đầu chạy. Nhưng Thỏ vẫn chủ quan, cứ Rùa chạy 3 bước thì Thỏ mới chạy 1 bước (1 bước Thỏ vẫn bằng 8 bước Rùa). Hỏi ai đến đích trước?
Bài 8. Lúc 8 giờ, một ô tô khởi hành để đi từ A đến B. Đến 9 giờ thì có ô tô thứ hai cũng đi từ A đến B và đến B sớm hơn ô tô thứ nhất 30 phút. Hỏi địa điểm hai ô tô gặp nhau cách A bao nhiêu ki-lô-mét? Biết ô tô thứ nhất đến B lúc 14 giờ và vận tốc ô tô thứ hai lớn hơn vận tốc ô tô thứ nhất là 20 km/giờ.
Bài 9. Một người đi xe đạp, một người đi xe máy và một người đi ô tô cùng đi từ A đến B, khởi hành lần lượt lúc 7 giờ; 8 giờ và 9 giờ với vận tốc theo thứ tự là 10 km/giờ; 30 km/giờ và 50 km/giờ. Hỏi đến mấy giờ thì ô tô ở vị trí chính giữa xe đạp và xe máy?
Bài 10. Hai anh em xuất phát cùng lúc ở điểm Y và chạy cùng chiều trên một đường tròn, anh chạy nhanh hơn. Anh gặp em lần thứ hai tại điểm Y. Biết em chạy đúng 1 vòng và hết 2 phút, còn anh chạy được quãng đường dài hơn em 400m. Tính vận tốc của mỗi người.
Bài 11. Hai anh em cùng xuất phát một lúc ở một vạch đích và chạy ngược chiều nhau trên một đường đua xung quanh một cái sân vận động. Anh chạy nhanh hơn em và khi anh chạy được 900m thì gặp em lần thứ nhất. Họ tiếp tục chạy như vậy và anh gặp em lần thứ hai và lần thứ ba. Đúng lần gặp nhau lần thứ ba thì họ dừng lại ở đúng điểm xuất phát. Biết rằng người em đã chạy hết 9 phút. Tìm vận tốc của mỗi người.
Bài 12. Việt và Nam chạy thi vòng quanh hồ. Việt chạy nhanh hơn nên vượt Nam ngay từ đầu và sau 35 phút thì gặp nhau lần thứ nhất. Biết Nam chạy một vòng hết 1 phút 45 giây, hỏi Việt chạy một vòng hết bao nhiêu thời gian?
Bài 13. Một xe tải đi từ A đến B với vận tốc 40 km/giờ. Sau đó một thời gian, một xe du lịch rời A với vận tốc 60 km/giờ và như vậy sẽ đến B cùng lúc với xe tải. Nhưng đi đến C, được 1/5 quãng đường AB, xe tải giảm vận tốc xuống còn 35 km/giờ, do đó xe du lịch gặp xe tải ở D, cách B 30km. Tính độ dài quãng đường AB.
Bài 14. Trên quãng đường AB, hai xe ô tô đi từ A và B ngược chiều nhau. Nếu hai xe khởi hành cùng lúc thì chúng gặp nhau tại một điểm cách A 12km, cách B 18km. Nếu muốn gặp chính giữa quãng đường thì xe đi từ A phải khởi hành trước xe đi từ B 10 phút. Tính vận tốc mỗi xe.
Bài 15. Hàng ngày ông Thanh đi làm vào buổi sáng và trở về nhà vào buổi chiều bằng xe buýt hoặc taxi. Nếu ông đi taxi vào buổi sáng thì buổi chiều sẽ về bằng xe buýt và nếu về nhà bằng taxi lúc buổi chiều thì sáng hôm đó đi làm bằng xe buýt. Trong x ngày đi làm, ông đi xe buýt vào buổi sáng 8 lần, về nhà bằng xe buýt 15 lần và đi taxi tất cả 9 lần. Hãy tìm x.
Bài 16. Có hai con ốc sên A và B. Cả hai cùng xuất phát bắt đầu từ X đến Y. A bò với vận tốc không đổi là 12 m/giờ cho đến khi nó đến được Y. Trong 4 giờ đầu, B bò với vận tốc 8 m/giờ nhưng sau đó nó thấy mình bị A bỏ lại đằng sau nên cố gắng bò nhanh hơn với vận tốc 20 m/giờ. B đã đuổi kịp rồi vượt qua A. Sau 2 giờ kể từ lúc gặp A thì B đến được Y.
a) Hỏi tính từ khi rời khỏi X, B đuổi kịp A sau bao lâu?
b) Tính thời gian B đi hết quãng đường XY.
c) Tính độ dài quãng đường XY.
Bài 17. Một ca nô xuôi dòng sông từ A đến B dài 150km. Khởi hành lúc 6 giờ 30 phút với vận tốc khi nước yên lặng là 45 km/giờ. Hôm sau lúc 8 giờ cũng với vận tốc đó, ca nô ngược dòng từ B về A. Cả đi và về người trên ca nô thấy đi ngang qua cây cầu cùng một giờ. Hỏi ca nô đi qua cầu lúc mấy giờ? Biết vận tốc dòng nước là 5 km/giờ.
Bài 18. Mai đi từ A và Linh đi từ B cùng xuất phát hướng về phía nhau, Linh có vận tốc lớn hơn Mai. Họ gặp nhau ở một vị trí cách A một khoảng 6km và tiếp tục hành trình của mình. Khi Mai đến B, cô ấy lập tức lái xe quay ngược trở về A và gặp Linh cũng lập tức lái xe từ A trở về B. Lần này hai người gặp nhau ở vị trí cách B một khoảng 4km. Tính độ dài quãng đường AB.
Bài 19. Quãng đường AB dài 48km. Cùng một lúc, một xe đạp xuất phát từ A đi đến B và một xe máy xuất phát từ B đi đến A. Hai xe gặp nhau lần đầu tại điểm C cách A một khoảng 12km. Đến A xe máy nghỉ 1 giờ 20 phút rồi quay lại đuổi theo xe đạp vẫn đang trên đường đi đến B. Hai xe gặp nhau lần thứ hai tại đúng điểm B. Tính vận tốc trung bình của mỗi xe.
Bài 20. Ô tô thứ nhất đi từ A đến B với vận tốc 40 km/giờ. Lát sau, ô tô thứ hai cũng đi từ A với vận tốc 52 km/giờ để gặp ô tô thứ nhất tại B. Ô tô thứ nhất đi được 2 giờ thì hư máy phải sửa trong 30 phút. Sửa xong nó đi với vận tốc 48 km/giờ, vì thế ô tô thứ hai gặp ô tô thứ nhất tại D, cách B 26km. Tính độ dài quãng đường AB.
Hi vọng các dạng toán chuyển động lớp 5 cơ bản và nâng cao kèm đáp án ở trên đã giúp các em hiểu rõ hơn về cách áp dụng các công thức tính toán liên quan đến quãng đường, vận tốc và thời gian.
Các dạng toán này được trình bày rất chi tiết trong cuốn 250+ bài toán chọn lọc lớp 5 (bao gồm cả đáp án). Các em hãy mua ngay cuốn sách này để học tốt môn Toán hơn nhé!
Link đọc thử sách: https://drive.google.com/file/d/1EnnjMiJ4MNEGPFR-Ar9WSRiPIzcLcBaQ/view
Link đặt mua sách để được giảm giá lên tới 30%:



