Bất đẳng thức và bất phương trình – Lý thuyết, bài tập và cách giải cực chi tiết

Bất đẳng thức và bất phương trình là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong 40% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.

Dưới đây là toàn bộ kiến thức về bất đẳng thức và bất phương trình. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!

I. BẤT ĐẲNG THỨC

1. Ôn tập bất đẳng thức

a. Khái niệm bất đẳng thức

Các mệnh đề dạng “a < b” hoặc “a > b” được gọi là bất đẳng thức.

b. Bất đẳng thức hệ quả và bất đẳng thức tương đương

Nếu mệnh đề “a < b => c < d’” đúng thì ta nói bất đẳng thức c < d là bất đẳng thức hệ quả của bất đăng thức a < b và cũng viết là a < b => c < d.

Nếu bất đẳng thức a < b là hệ quả của bất đăng thức c < d và ngược lại thì ta nói hai bất đẳng thức tương đương với nhau và viết là a < b ⇔ c < d.

c. Tính chất của bất đẳng thức

Như vậy để chứng minh bất đẳng thức a < b ta chỉ cần chứng minh a – b < 0. Tổng quát hơn, khi so sánh hai số, hai biểu thức hoặc chứng minh một bất đẳng thức, ta có thể sử dụng các tính chất của bất đẳng thức được tóm tắt trong bảng sau:

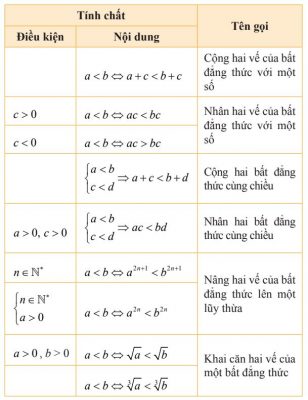
Chú ý: Ta còn gặp các mệnh đề dạng a ≤ b hoặc a ≥ b. Các mệnh đề dạng này cũng được gọi là bất đẳng thức. Để phân biệt, ta gọi chúng là các bất đẳng thức không ngặt và gọi các bất đẳng thức dạng a < b hoặc a > b là các bất đẳng thức ngặt.

Các tính chất nêu trong bảng trên cũng đúng cho bất đẳng thức không ngặt.

2. Bất đẳng thức giữa trung bình công và trung bình nhân (bất đẳng thức Cô-si)

a. Bất đẳng thức Cô-si

Định lí: Trung bình nhân của hai số không âm nhỏ hơn hoặc bằng trung bình cộng của chúng.

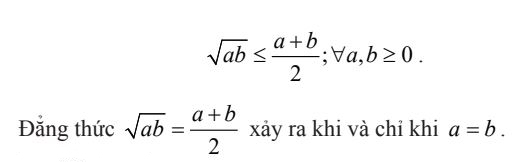
b. Các hệ quả

+ Hệ quả 1

Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2

a + 1/a ≥ 2; ∀a > 0

+ Hệ quả 2

Nếu x, y cùng dương và có tổng không đổi thì tích xy lớn nhất khi và chỉ khi x = y.

+ Hệ quả 3

Nếu x,y cùng dương và có tích không đổi thì tổng x + y nhỏ nhất khi và chỉ khi x = y.

3. Bất đẳng thức chúa cấu giá trị tuyệt đối\

Điều kiện	Nội dung
a > 0	|x| ≥ 0, |x| ≥ x, |x| ≥ -x
	|x| ≤ a ⇔ -a ≤ x ≤ a
	|x| ≥ a ⇔ x ≤ -a hoặc x ≥ a
	|a| – |b| ≤ |a + b| ≤ |a| + |b|

II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN

1. Khái niệm bất phương trình một ẩn

a. Bất phương trình một ẩn

Bất phương trình ẩn x là mệnh đề chứa biến có dạng f(x) < g(x) (f(x) ≤ g(x)) (1).

trong đó f(x) và g(x) là những biểu thức của x

Ta gọi f(x) và g(x) lần lượt là về trái và về phải của bất phương trình (1).

Số thực x₀ sao cho f(x₀) < g(x₀) (f(x₀) ≤ g(x₀)) là mệnh đề đúng được gọi là một nghiệm của bất phương trình (1).

Giải bất phương trình là tìm tập nghiệm của nó, khi tập nghiệm rỗng thì ta nói bất phương trình vô nghiệm.

Chú ý: Bất phương trình (1) cũng có thể viết lại dưới dạng sau:

g(x) > f(x) (g(x) ≥ f(x)).

b. Điều kiện của một bất phương trình

Tương tự đối với phương trình, ta gọi các điều kiện của ẩn số x để f(x) và g(x) có nghĩa là điều kiện xác định (hay gọi tắt là điều kiện) của bất phương trình (1).

c. Bất phương trình chứa tham số

Trong một bất phương trình, ngoài các chữ đóng vai trò ẩn số còn có thể có các chữ khác được xem như những hằng số và được gọi là tham số. Giải và biện luận bất phương trình chứa tham số là xét xem với các giá trị nào của tham số bất phương trình vô nghiệm, bất phương trình có nghiệm và tìm các nghiệm đó.

2. Hệ bất phương trình một ấn

Hệ bất phương trình ẩn x gồm một số bất phương trình ẩn x mà ta phải tìm nghiệm chung của chúng.

Mỗi giá trị của x đồng thời là nghiệm của tất cả các bất phương trình của hệ được gọi là một nghiệm của hệ bất phương trình đã cho.

Giải hệ bất phương trình là tìm tập nghiệm của nó.

Để giải một hệ bất phương trình ta giải từng bất phương trình rồi lấy giao của các tập nghiệm.

3. Một số phép biến đổi bất phương trình

a. Bất phương trình tương đương

Ta đã biết hai bất phương trình có cùng tập nghiệm (có thể rỗng) là hai bất phương trình tương đương và dùng kí hiệu “⇔” để chỉ sự tương đương của hai bất phương trình đó.

Tương tự, khi hai hệ bất phương trình có cùng một tập nghiệm ta cũng nói chúng tương đương với nhau và dùng kí hiệu “⇔” để chỉ sự tương đương đó.

b. Phép biến đổi tương đương

Để giải một bất phương trình (hệ bất phương trình) ta liên tiếp biến đổi nó thành những bất phương trình (hệ bất phương trình) tương đương cho đến khi được bất phương trình (hệ bất phương trình) đơn giản nhất mà ta có thể viết ngay tập nghiệm. Các phép biến đổi như vậy được gọi là các phép biến đổi tương đương.

c. Cộng (trừ)

Cộng (trừ) hai vế của bất phương trình với cùng một biểu thức mà không làm thay đổi điều kiện của bất phương trình ta được một bất phương trình tương đương.

P(x) < Q(x) ⇔ P(x) + f(x) < Q(x) + f(x)

d. Nhân (chia)

P(x) < Q(x) ⇔ P(x).f(x) < Q(x).f(x), f(x) > 0, ∀x

P(x) < Q(x) ⇔ P(x).f(x) > Q(x).f(x), f(x) < 0, ∀x

e. Bình phương

Bình phương hai vế của một bất phương trình có hai vế không âm mà không làm thay đổi điều kiện của nó ta được một bất phương trình tương đương.

P(x) < Q(x) ⇒ P²(x) < Q²(x), P(x) ≥ 0, Q(x) ≥0, ∀x

f. Chú ý

Trong quá trình biến đổi một bất phương trình thành bất phương trình tương đương cần chú ý những điều sau:

• Khi biến đổi các biểu thức ở hai vế của một bất phương trình thì điều kiện của bất phương trình có thể bị thay đổi. Vì vậy, để x thỏa mãn điều kiện ban đầu của bất phương trình đó và là nghiệm của bất phương trình mới.
• Khi nhân (chia) hai vế của bất phương trình P(x) < Q(x) với biểu thức f(x) ta cần lưu ý đến điều kiện về dấu của f (x) . Nếu f(x) nhận cả giá trị dương lẫn giá trị âm thì ta phải lần lượt xét từng trường hợp. Mỗi trường hợp dẫn đến hệ bất phương trình.

Khi giải bất phương trình P(x )< Q(x) mà phải bình phương hai vế thì ta lần lượt xét hai trường hợp:

• P(x), Q(x) cùng có giá trị không âm, ta bình phương hai vế bất phương trình.
• P(x), Q(x) cùng có giá trị âm ta viết P(x) < Q(x) ⇔ -Q(x) < -P(x) rồi bình phương hai vế bất phương trình mới.

III. DẤU CỦA NHỊ THỨC BẬC NHẤT

1. Định lí về dấu của nhị thức bậc nhất

a. Nhị thức bậc nhất

Nhị thức bậc nhất ẩn x có dạng f(x) = ax + b trong đó a,b ∈ R, a ≠ 0.

b. Dấu của nhị thức bậc nhất

Định lí

Nhị thức f (x) = ax + b có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng (-b/a;+∞), trái dấu với hệ số a khi x lấy giá trị trong khoảng (-∞;-b/a).

x	-∞	-b/a	+∞
f (x) = ax + b	trái dấu với a	0	Cùng dấu với a

Minh họa bằng đồ thị:

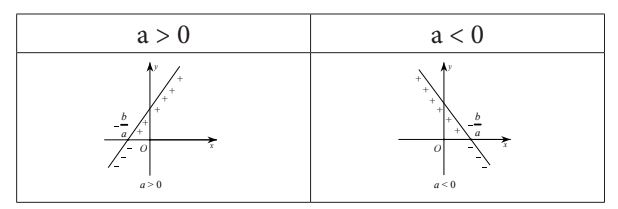
2. Xét dấu tích thương các nhị thức bậc nhất

Giả sử f(x) là một tích của những nhị thức bậc nhất. Áp dụng định lí về dấu của nhị thức bậc nhất có thể xét dấu từng nhân tử.

Lập bảng xét dấu chung cho tất cả các nhị thức bậc nhất có mặt trong f(x) ta suy ra được dấu của f(x). Trường hợp f(x) là một thương cũng được xét tương tự.

3. Áp dụng vào giải bất phương trình

Giải bất phương trình f(x) > 0 thực chất là xét xem biểu thức f(x) nhận giá trị dương với những giá trị nào của x (do đó cũng biết f(x) nhận giá trị âm với những giá trị nào của x), làm như vậy ta nói đã xét dấu biểu thức f(x).

a. Bất phương trình tích, bất phương trình chứa ẩn ở mẫu

b. Bất phương trình chứa dấu giá trị tuyệt đối

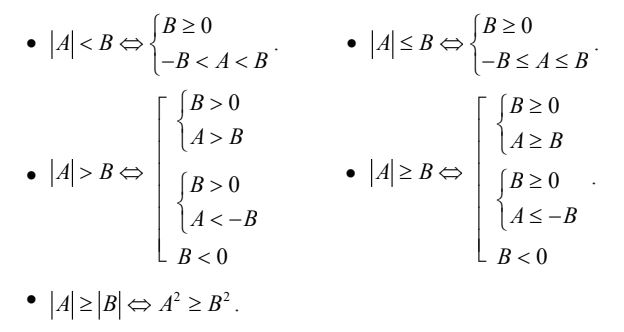
c. Bất phương trình chứa căn thức và dấu giá trị tuyệt đối

d. Các bất phương trình khác

IV. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

1. Bất phương trình bậc nhất hai ẩn

Bất phương trình bậc nhất hai ẩn x,y có dạng tổng quát là ax + by ≤ c (1).

hoặc (ax + by < c; ax + by ≥ c; ax + by > c)

trong đó x, y là hai ẩn; a, b, c là các hệ số (với a² + b² > 0).

2. Biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn

Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình (1) được gọi là miền nghiệm của nó.

Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình ax + by ≤ c như sau (tương tự cho bất phương trình ax + by > c )

• Bước 1. Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng A: ax + by = c.
• Bước 2. Lấy một điểm M(x₀;y₀) ∈ Δ (ta thường lấy gốc tọa độ 0)
• Bước 3. Tính ax₀ + by₀, và so sánh ax₀ + by₀ với c
• Bước 4. Kết luận

+ Nếu ax₀ + by₀ < c thì nửa mặt phẳng bờ A chứa M, là miền nghiệm của ax₀ + by₀ ≤ c.

+ Nếu ax₀ + by₀ > c thì nửa mặt phẳng bờ A không chứa M, là miền nghiệm của ax₀ + by_{0 ≥} c.

Chú ý:

Miền nghiệm của bất phương trình ax₀ + by₀ ≤ c bỏ đi đường thẳng ax + by = c là miền nghiệm của bất phương trình ax₀ + by₀ > c.

+ Ví dụ:

Biểu diễn hình học tập nghiệm của bất phương trình 2x + y ≤ 3.

Lời giải

Vẽ đường thẳng A:2x + y = 3.

Lấy gốc tọa độ O(0;0), ta thấy O ∉ Δ và có 2.0 + 0 < 3 nên nửa mặt phẳng bờ A chứa gốc tọa độ O là miền nghiệm của bất phương trình đã cho (miền không bị tô đậm trong hình).

3. Hệ bất phương trình bậc nhất hai ẩn

Tương tự hệ bất phương trình một ẩn.

Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn x,y mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.

Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.

+ Ví dụ:

Biểu diễn hình học tập nghiệm của hệ bất phương trình:

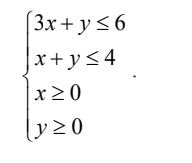
Lời giải

Vẽ các đường thẳng:

• d₁:3x + y = 6
• d₂ : x + y = 4
• d₂: x = 0 (Oy)
• d₂: y = 0 (Ox)

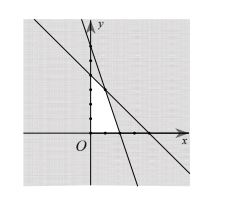
Vì điểm M₀(1;1) có tọa độ thỏa mãn tất cả các bất phương trình trong hệ trên nên ta tô đậm các nửa mặt phẳng bờ (d,), (d,), (d,), (d,) không chứa điểm M . Miền không bị tô đậm (hình tứ giác OCIA kể cả bốn cạnh AI, IC, CO, OA) trong hình vẽ là miền nghiệm của hệ đã cho.

V. DẤU CỦA TAM THÚC BẬC HAI

1. Định lí về dấu của tam thức bậc hai

a. Tam thức bậc hai

Xét tam thức bậc hai ẩn x có dạng f(x) = ax’+ bx + c , trong đó a,b,c ∈ R, a≠0.

b. Dấu của tam thức bậc hai

Người ta đã chứng minh được định lí về dấu tam thức bậc hai sau đây:

Định lý:

Cho f(x) = ax² + bx + c (a≠0); Δ = b² – 4ac

+ Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ R

+ Nếu Δ = 0 thì f(x) luôn cùng dấu với hệ số a, trừ khi x = -b/2a

+ Nếu Δ > 0 thì f(x) luôn cùng dấu với hệ số a khi x < x₁ hoặc x > x₂ , trái dấu với hệ số a khi x₁ < x < x₂, trong đó x₁, x₂ ( x₁ <x₂) là hai nghiệm của f(x) .

• Chú ý: Trong định lí trên, có thể thay biệt thức Δ = b² – 4ac bằng biệt thức thu gọn Δ’ = (b’)² – ac

+ Minh họa hình học

Định lí về dấu của tam thức bậc hai có minh họa hình học sau:

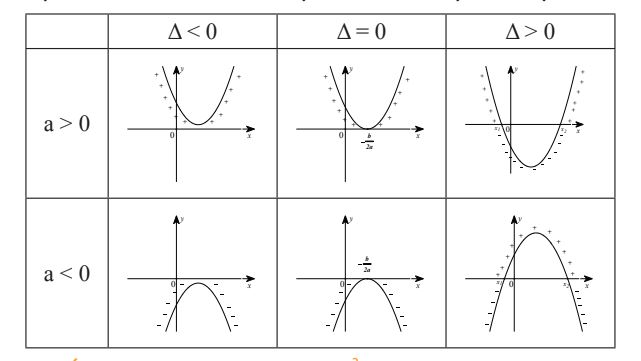
2. Bất phương trình bậc hai một ẩn

d. Bất phương trình bậc hai

Bất phương trình bậc hai ẩn x là bất phương trình dạng:

ax² + bx + c < 0 (hoặc ax² + bx + c ≤ 0, ax² + bx + c > 0, ax² + bx + c ≥ 0), trong đó a,b,c ∈ R; a≠0.

e. Giải bất phương trình bậc hai

Giải bất phương trình bậc hai ax² + bx + c < 0 thực chất là tìm các khoảng mà trong đó f(x)= ax² + bx + c cùng dấu với hệ số a (trường hợp a < 0) hay trái dấu với hệ số a (trường hợp a>0).

f. Một số điều kiện tương đương

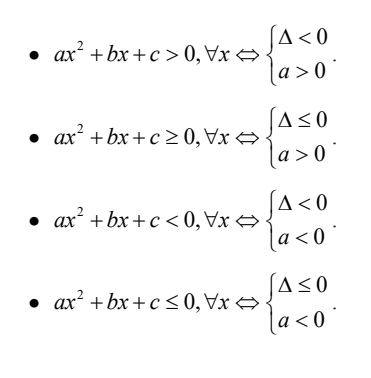
VI. Một số bài tập về bất đẳng thức và bất phương trình

Dưới đây là một số dạng toán cơ bản về bất đẳng thức và bất phương trình để các em luyện tập và ôn luyện kiến thức:

Các dạng toán khác về bất đẳng thức và bất phương trình được ghi chú và diễn giải rất đầy đủ trong cuốn  cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!

Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.

Tkbooks.vn