Tính diện tích hình thang biết 4 cạnh – Phương pháp giải chi tiết dễ hiểu

Tính diện tích hình thang biết 4 cạnh là một dạng toán quan trọng trong chương trình Toán THCS và THPT, thường xuyên xuất hiện trong các bài kiểm tra, bài thi học kỳ cũng như đề thi tuyển sinh. Tuy nhiên, nhiều học sinh gặp khó khăn khi làm dạng toán này vì trong công thức tính diện tích hình thang, chỉ biết 4 cạnh là chưa đủ, mà còn cần phải có chiều cao h của hình thang.

Vậy khi đề bài không cho sẵn chiều cao, chúng ta phải làm thế nào để tính được diện tích?

Trong bài viết này, chúng ta sẽ cùng tìm hiểu cách tính diện tích hình thang khi biết 4 cạnh, thông qua việc phân tích hình học, áp dụng định lý Pitago và làm rõ từng bước giải cụ thể.

Mời các em tham khảo!

1. Ôn lại công thức diện tích hình thang

Công thức diện tích hình thang là:

Trong đó:

• a là độ dài đáy lớn
• b là độ dài đáy nhỏ
• h là chiều cao của hình thang

♦ Vấn đề đặt ra: Khi đề bài chỉ cho 4 cạnh của hình thang, ta chưa biết chiều cao h nên chưa thể áp dụng trực tiếp công thức trên. Do đó, bước quan trọng nhất là tìm chiều cao của hình thang.

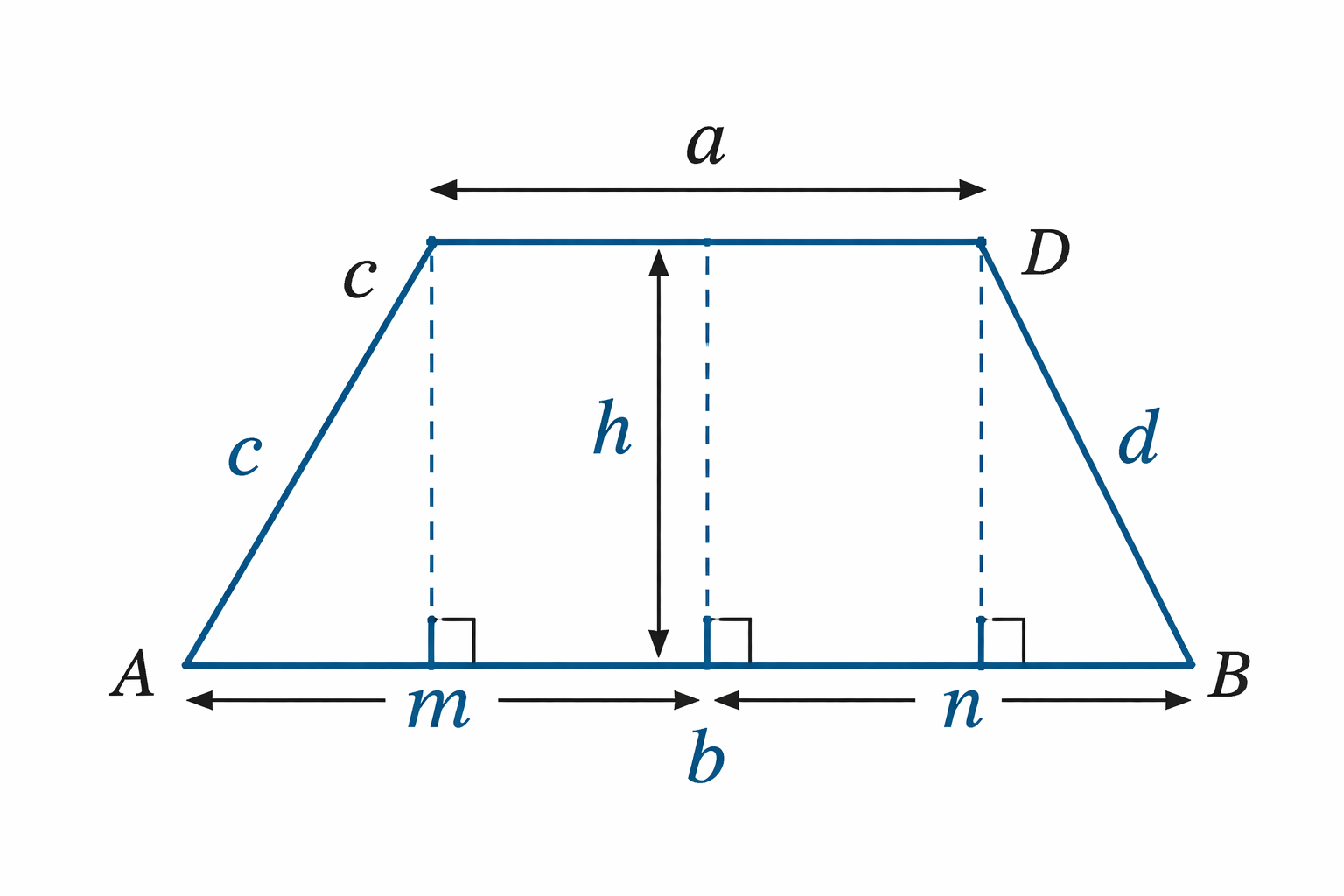
2. Cách tính diện tích hình thang khi biết 4 cạnh

Tìm chiều cao bằng định lý Pitago:

♦ Bước 1: Tính hiệu hai đáy

x = a – b

♦ Bước 2: Kẻ đường cao

Kẻ đường cao từ đáy nhỏ xuống đáy lớn, ta được:

Hai tam giác vuông ở hai bên

Gọi:

m là hình chiếu của cạnh c lên đáy lớn

n là hình chiếu của cạnh d lên đáy lớn

Ta có:

m + n = a – b

♦ Bước 3: Lập hệ phương trình

Từ định lý Pitago, ta có:

• c² = h² + m²
• d² = h² + n2²

Trừ hai phương trình ta có:

c² – d² = m² – n² = (m − n)(m + n)

Suy ra: m − n = (c² – d²)/a – b)

♦ Bước 4: Giải hệ phương trình và tìm m, n

• ​m + n = a – b
• m − n = (c² – d²)/a – b)

♦ Bước 5: Tính chiều cao:

h = √(c² – m²)

Lưu ý:

• Bốn cạnh của hình thang phải thỏa mãn điều kiện tạo thành hình thang
• Nếu tính ra h không phải số thực thì dữ liệu đề bài không hợp lệ
• Nên ưu tiên trình bày từng bước rõ ràng khi làm bài thi

3. Ví dụ

Cho hình thang có:

• Đáy lớn a = 14
• Đáy nhỏ b = 8
• Hai cạnh bên c = d = 5

Hãy tính diện tích hình thang.

Lời giải:

Áp dụng từng bước trên, ta có lời giải như sau:

Bước 1: Tính hiệu hai đáy

a – b = 14 – 8 = 6

Bước 2: Xác định các đoạn chiếu

Do hai cạnh bên của hình thang bằng nhau (c = d = 5) nên hình thang đã cho là hình thang cân.

Ta có:

m = n = (a – b)/2 ​= 6/2 ​= 3

Bước 3: Tính chiều cao

Áp dụng định lý Pitago, ta tính được:

h = √(c² – m²) = √(5² – 3²) = √(25 – 9) = √16 = 4

Bước 4: Tính diện tích hình thang

Vậy diện tích của hình thang đã cho là:

S = [(a + b) x h]/2 = [(14 + 8) x 4]/2 = 88/2 = 44

4. Bài tập vận dụng

♦ Bài 1: Cho hình thang có:

• Đáy lớn a = 12
• Đáy nhỏ b = 6
• Hai cạnh bên c = d = 5

Hãy tính diện tích của hình thang trên.

♦ Bài 2: Cho hình thang có:

• Đáy lớn a = 15
• Đáy nhỏ b = 9
• Hai cạnh bên c = 6, d = 8

Hãy tính diện tích của hình thang trên.

♦ Bài 3: Cho hình thang có:

• Đáy lớn a = 18
• Đáy nhỏ b = 10
• Hai cạnh bên c = 7, d = 9

a, Kiểm tra xem bốn cạnh đã cho có tạo thành hình thang hay không.

b, Nếu có, hãy tính diện tích hình thang.

Hy vọng hướng dẫn tính diện tích hình thang biết 4 cạnh ở trên đã giúp các em hiểu rõ bản chất của dạng toán này cũng như nắm vững các bước giải từ việc tìm chiều cao đến áp dụng công thức tính diện tích. Khi gặp bài toán chỉ cho 4 cạnh, các em không nên vội vàng mà cần phân tích hình học, vận dụng linh hoạt định lý Pitago và trình bày lời giải một cách khoa học, rõ ràng.

Việc thường xuyên luyện tập các bài toán tính diện tích hình thang biết 4 cạnh sẽ giúp các em nâng cao kỹ năng tư duy, tránh sai sót trong quá trình làm bài và tự tin hơn khi bước vào các bài kiểm tra, bài thi quan trọng. Chúc các em học tốt và đạt kết quả cao trong môn Toán!

Để luyện thêm các dạng hình học như hình thang, tam giác, diện tích và các bài tập để đạt điểm cao trong kiểm tra, các em có thể tham khảo các cuốn sách như Bài tập bổ trợ nâng cao Toán lớp 5, 50 đề tăng điểm nhanh Toán lớp 5 của TKbooks nhé!

Link đọc thử sách: https://drive.google.com/file/d/1bD2vpRYqsx_Sqyi5Ww72Bgb4i58BrziO/view?usp=sharing

TKbooks tự hào là nhà xuất bản sách tham khảo lớp 5 hàng đầu tại Việt Nam!

TKbooks.vn