5 cách chứng minh 4 điểm cùng thuộc một đường tròn lớp 9 kèm ví dụ

Để chứng minh 4 điểm cùng thuộc một đường tròn (hay còn gọi là chứng minh tứ giác nội tiếp), chúng ta thường sử dụng các phương pháp phổ biến dựa trên tính chất hình học phẳng sau đây:

1. Chứng minh các điểm cùng cách đều một điểm cố định

Đây là định nghĩa cơ bản nhất. Nếu bạn tìm được một điểm O sao cho khoảng cách từ O đến cả 4 điểm A, B, C, D đều bằng nhau, thì 4 điểm đó cùng nằm trên đường tròn tâm O.

♦ Cách làm: Chứng minh OA = OB = OC = OD = R.

Ví dụ:

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh rằng bốn điểm A, B, C và điểm D đối xứng với A qua M cùng thuộc một đường tròn.

Lưu ý: Đây là một ví dụ điển hình và cơ bản nhất để áp dụng phương pháp chứng minh các điểm cùng cách đều một điểm cố định. Dạng bài này thường xuất hiện với các tam giác vuông.

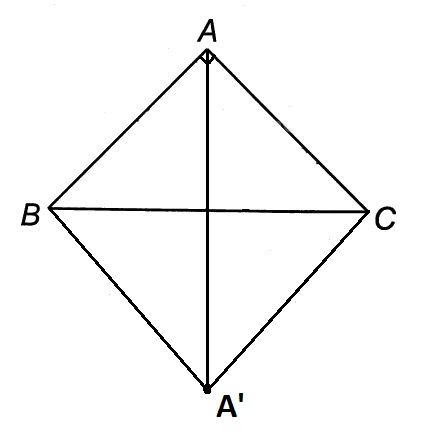
Giải:

Tam giác ABC vuông tại A, M là trung điểm BC. Theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có:

MA = MB = MC = 1/2BC

Điểm D đối xứng với A qua M. Điều này có nghĩa là M là trung điểm của đoạn thẳng AD, hay:

MA = MD

Từ hai điều trên, ta có hệ thức sau:

MA = MB = MC = MD

Vì cả bốn điểm A, B, C, D đều cách đều điểm M một khoảng bằng nhau, nên chúng cùng nằm trên đường tròn tâm M, bán kính R = MA.

Mở rộng: Trong bài toán này, tứ giác ABCD thực chất là một hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau). Một trong những tính chất quan trọng của hình chữ nhật là luôn nội tiếp một đường tròn có tâm là giao điểm của hai đường chéo.

2. Chứng minh tổng hai góc đối bằng 180°

Đây là phương pháp phổ biến nhất khi làm bài tập về tứ giác nội tiếp.

♦ Cách làm: Xét tứ giác ABCD, nếu bạn chứng minh được:

Góc A + Góc C = 180° hoặc Góc B + Góc D = 180° thì tứ giác đó nội tiếp đường tròn.

Ví dụ:

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh rằng bốn điểm A, B, C và điểm D đối xứng với A qua M cùng thuộc một đường tròn.

Lưu ý: Đây là một ví dụ kinh điển thường xuất hiện trong các đề thi Hình học lớp 9. Bài toán này sử dụng các đường cao của tam giác để tạo ra các góc vuông, từ đó dẫn đến tổng các góc đối bằng 180°.

Giải:

Để chứng minh tứ giác BCDE nội tiếp, ta có thể chứng minh tổng hai góc đối bằng 180°.

Ta có: BD và CE là đường cao nên chúng tạo ra các góc 90°.

Xét tứ giác ADHE (với H là giao điểm của BD và CE):

Vì BD ⊥ AC (giả thiết) ⇒ ADH = 90°.

Vì CE ⊥ AB (giả thiết) ⇒ AEH = 90°.

Xét tứ giác ADHE có tổng hai góc đối: góc ADH + góc AEH = 90° + 90° = 180° nên tứ giác ADHE nội tiếp trong một đường tròn (theo dấu hiệu nhận biết tứ giác nội tiếp).

3. Chứng minh hai đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau

Nếu hai đỉnh cùng nằm về một phía của đoạn thẳng nối hai đỉnh còn lại và cùng nhìn đoạn thẳng đó dưới một góc α không đổi.

♦ Cách làm: Xét tứ giác ABCD, nếu góc ADB = góc ACB, thì 4 điểm A, B, C, D cùng thuộc một đường tròn. (Người ta thường gọi đây là phương pháp “cung chứa góc”).

Ví dụ:

Cho tam giác ABC cân tại A. Các đường phân giác BD và CE (D ∈ AC, E ∈ AB). Chứng minh rằng tứ giác BCDE nội tiếp một đường tròn.

Lưu ý: Đây là phương pháp cực kỳ hiệu quả để chứng minh các tứ giác tạo bởi đường cao hoặc các tam giác đặc biệt. Dấu hiệu nhận biết là bạn thấy hai tam giác có chung một cạnh đáy và có hai góc ở đỉnh bằng nhau.

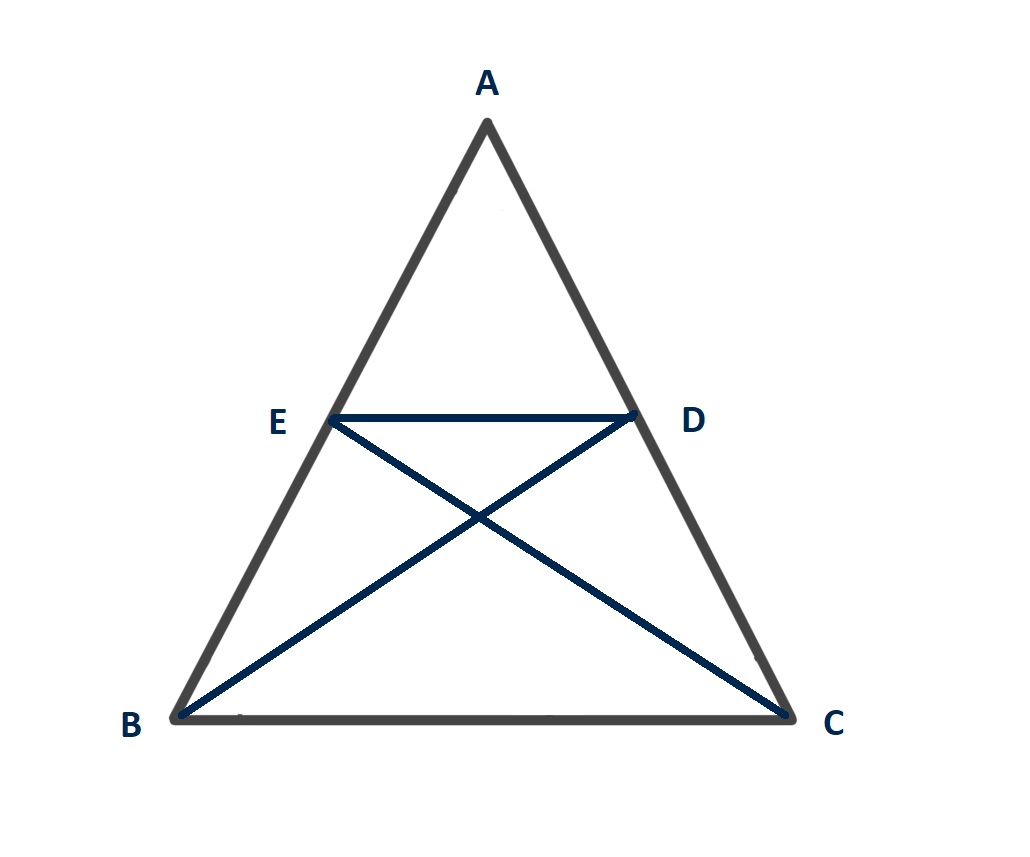
Giải:

Ta có:

Tam giác ABC cân tại A ⇒ góc ABC = góc ACB.

BD là phân giác của góc ABC ⇒ góc CBD = ½ góc ABC.

CE là phân giác của góc ACB ⇒ góc BCE = ½ góc ACB.

Từ đó suy ra: Góc CBD = góc BCE.

Xét tứ giác BCDE, ta có hai đỉnh D và E là hai đỉnh kề nhau.

Cả hai đỉnh này cùng nhìn cạnh đối diện là BC.

Xét tam giác BCD và tam giác CBE có:

BC là cạnh chung.

Góc BCD = góc CBE (do tam giác ABC cân).

BD = CE (tính chất đường phân giác trong tam giác cân).

⇒ tam giác BCD = tam giác CBE$ (c.g.c).

⇒ Góc BDC = góc CEB.

Vì hai đỉnh E và D cùng nhìn cạnh BC dưới hai góc bằng nhau (góc BEC = góc CDB), nên tứ giác BCDE nội tiếp đường tròn.

4. Chứng minh góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện

Đây thực chất là hệ quả của phương pháp thứ 2.

♦ Cách làm: Nếu góc ngoài tại đỉnh A của tứ giác ABCD bằng góc trong tại đỉnh C, thì tứ giác đó nội tiếp.

Ví dụ:

Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Trên tia đối của tia AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho BM = CN. Chứng minh rằng tứ giác BCNM nội tiếp một đường tròn.

Giải:

Vì tam giác ABC cân tại A nên góc ABC = góc ACB.

Xét góc ngoài tại đỉnh B của tứ giác BCNM. Góc này chính là góc ABC (do M nằm trên tia đối của AB, nên góc MBC là góc trong, và góc kề bù với nó quay lại chính là góc ABC).

Xét tam giác AMN:

Vì AB = AC (do tam giác ABC cân) và BM = CN (giả thiết) nên:

AM = AB + BM = AC + CN = AN

⇒ tam giác AMN cân tại A.

Do cả tam giác ABC và tam giác AMN đều cân tại A nên:

Góc ABC = (180° – góc A)/2

Góc ANM = (180° – góc A)/2

⇒ Góc ABC = góc ANM (hay góc ABC} = góc CNM).

Trong tứ giác BCN, ta có góc ngoài tại đỉnh B (là góc ABC) bằng góc trong tại đỉnh đối diện N (là góc CNM).

Vậy tứ giác BCNM nội tiếp một đường tròn.

5. Sử dụng các hệ thức lượng (Phương tích)

Nếu hai đường thẳng chứa hai cạnh đối hoặc hai đường chéo cắt nhau tại một điểm, ta có thể dùng tỉ lệ độ dài.

• Cắt nhau tại hai đường chéo: Nếu AC cắt BD tại E và EA x EC = EB x ED, thì 4 điểm A, B, C, D cùng thuộc một đường tròn.
• Cắt nhau ngoài tứ giác: Nếu AB và CD kéo dài cắt nhau tại M và MA x MB = MC x MD thì tứ giác ABCD nội tiếp.

Ví dụ:

Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE, CF cắt nhau tại trực tâm H. Chứng minh rằng tứ giác AFHE nội tiếp bằng cách sử dụng hệ thức lượng, từ đó suy ra HA x HD = HB x HE = HC x HF.

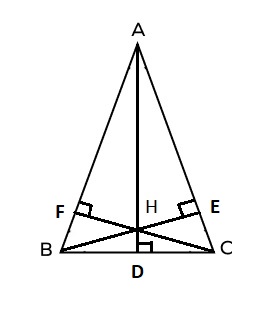
Giải:

Trong bài toán này, thực tế có rất nhiều tứ giác nội tiếp. Để sử dụng phương tích, chúng ta thường dựa vào các cặp tam giác đồng dạng được tạo bởi các đoạn thẳng cắt nhau tại một điểm.

Chứng minh tứ giác AFHE nội tiếp:

Ta có BE⊥AC ⇒ góc AEH = 90°.

Ta có CF⊥AB ⇒ góc AFH = 90°.

Xét tứ giác AFHE có góc AEH + góc AFH = 90° + 90° = 180°.

⇒Tứ giác AFHE nội tiếp đường tròn đường kính AH.

Sử dụng hệ thức lượng (Phương tích) để mở rộng:

Xét hai tam giác HFB và tam giác HEC có:

Góc HFB = góc HEC = 90°.

Góc FHB = góc EHC (hai góc đối đỉnh).

⇒ tam giác HFB đồng dạng với tam giác HEC (g.g).

Từ tỉ số đồng dạng, ta có: HF/HE = HB/HC

⇒ HB x HE = HC x HF (1)

Tương tự, xét tam giác HFA và tam giác HDB có:

Góc HFA = góc HDB = 90°

Góc FHA = góc DHB (đối đỉnh).

⇒ tam giác HFA đồng dạng với tam giác HDB (g.g).

⇒ HF/HD = HA/HB

⇒ HA x HD = HB x HF (2)

Từ (1) và (2), ta có hệ thức:

HA x HD = HB x HE = HC x HF

Lời khuyên: Khi làm bài, bạn nên ưu tiên kiểm tra Tổng hai góc đối hoặc Hai góc cùng nhìn một cạnh trước, vì đây là hai dấu hiệu xuất hiện trong 90% các bài thi hình học lớp 9.

Hy vọng 5 cách chứng minh 4 điểm cùng thuộc một đường tròn lớp 9 kèm ví dụ ở trên đã giúp các em tự tin hơn khi đối mặt với các bài toán về tứ giác nội tiếp đường tròn cũng như đạt điểm cao trong các bài thi và bài kiểm tra.

Đừng quên tham khảo thêm 2 cuốn Làm chủ kiến thức Toán 9 ôn thi vào 10 phần Đại số và Hình học để biết cách giải tất cả các bài toán trong chương trình lớp 9 nhé!

Link đọc thử phần Đại số: https://drive.google.com/file/d/1uaOJCek1Mpmm-UbFU3hEIVzQ0P6PPaoC/view

Link đọc thử phần Hình học: https://drive.google.com/file/d/162Yv0A_lC8XmgSN_AjwxVuKPWpbVVkJj/view

Nếu các em có bất kỳ thắc mắc nào, hãy để lại bình luận dưới bài viết để được giải đáp nhé!

Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 9 hàng đầu tại Việt Nam!

Tkbooks.vn