Chưa có sản phẩm trong giỏ hàng.
Các dạng bài tập Toán lớp 6 học kì 1 thường gặp nhất trong đề thi
Dưới đây là các dạng bài tập Toán lớp 6 học kì 1 thường gặp nhất trong đề thi, phân chia thành hai phần chính: Đại số và Hình học.
Các dạng bài tập này sẽ giúp học sinh làm quen với các khái niệm toán học cơ bản và phát triển kỹ năng tính toán, giải toán có lời văn, tìm x, tính tổng, chia hết, ước chung, bội chung, và nhiều nội dung thú vị khác, từ đó tự tin hơn khi làm các bài thi và bài kiểm tra môn Toán trên lớp.
Mời quý phụ huynh và các em học sinh tham khảo!
I. Phần Đại số
1. Tập hợp
Trong phần Tập hợp, các em sẽ phải mô tả về khái niệm tập hợp và cách thể hiện các tập hợp số. Học sinh sẽ làm quen với việc mô tả tập hợp bằng các cách khác nhau, sử dụng ký hiệu ∈ (thuộc) và ∉ (không thuộc), cũng như minh họa tập hợp bằng hình vẽ.
+ Mô tả tập hợp
Ví dụ: Viết tập hợp A các số tự nhiên lớn hơn 4 và không vượt qua 7 bằng hai cách.
+ Minh họa một tập hợp cho trước bằng hình vẽ
Ví dụ: Nhìn vào hình vẽ sau, hãy viết tập hợp A.
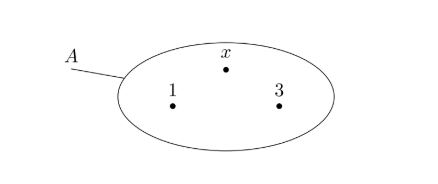
+ Sử dụng ký hiệu ∈, ∉
Ví dụ: Cho tập hợp B = {x| x là số tự nhiên, x < 10}.
Các phần tử 0; 1; 5; 10; 13 có thuộc tập hợp B không? Viết câu trả lời bằng cách sử dụng ký hiệu ∈, ∉.

2. Thực hiện phép tính
Học sinh sẽ thực hành các phép toán cơ bản như cộng, trừ, nhân, chia và tính lũy thừa với số mũ tự nhiên. Đây là phần cơ bản giúp củng cố kỹ năng tính toán và làm quen với việc áp dụng các phép toán vào bài toán cụ thể.
Ví dụ:
a) 3.52 + 15.22 – 26 : 2
b) 53.2 – 100 : 4 + 23.5
c) 62 : 9 + 50.2 – 33.3
3. Tìm x
Phần này giúp học sinh giải các phương trình đơn giản và tìm giá trị của ẩn x. Đây là một bước quan trọng trong việc phát triển khả năng giải toán đại số và áp dụng lý thuyết vào thực tế.
Ví dụ: Tìm x:
a) 165 : x = 3
b) x – 71 = 129
c) 22 + x = 52
d) 2x = 102
e) x + 19301
f) 93 – x = 27
4. Tính nhanh
Các phép tính cộng, trừ, nhân, chia đơn giản sẽ được thực hiện một cách nhanh chóng và hiệu quả, giúp học sinh rèn luyện khả năng tính toán nhanh chóng mà không cần sử dụng máy tính.
Ví dụ:
a) 58.75 + 58.50 – 58.25
b) 27.39 + 27.63 – 2.27
c) 128.46 + 128.32 + 128.22
d) 66.25 +5.66+ 66.14 + 33.66
e) 12.35 + 35.182 – 35.94
5. Tính tổng
Trong phần này, học sinh sẽ học cách tính tổng của một dãy số theo một quy luật nhất định, từ đó hiểu được cách tính tổng của dãy số hữu hạn và vô hạn.
Ví dụ: Tính tổng:
a) S1 = 1 + 2 + 3 + … + 999
b) S2 = 10 + 12 + 14 + … + 2010
c) S3 = 21 + 23 + 25 + … + 1001
d) S4 = 24 + 25 + 26 + … + 125 + 126
6. Dấu hiệu chia hết
Học sinh sẽ được làm quen với các dấu hiệu chia hết cho các số như 2, 5, 3, 9. Các bài toán giúp học sinh nhận diện số chia hết và làm quen với các phương pháp kiểm tra chia hết.
+ Nhận biết các số chia hết cho 2; 5; 3; 9
Ví dụ: Trong các số: 4827; 5670; 6915; 2007.
a) Số nào chia hết cho 3 mà không chia hết cho 9?
b) Số nào chia hết cho cả 2; 3; 5 và 9?
+ Tìm số chưa biết
Ví dụ: Thay * bằng các chữ số nào để được số 73* chia hết cho cả 2 và 9.
+ Chứng minh chia hết, chia dư
Ví dụ: 2007 + 1998 + 106 + 8 chia hết cho 9 không ? ( có giải thích )
+ Toán có lời văn
Ví dụ: Có 3 tờ giấy. Người ta xé các tờ giấy đó thành 4 mảnh. Tiếp tục lấy một mảnh trong đó, xé mỗi mảnh thành 4 mảnh. Cứ như vậy sau một số lần, người ta đếm được 205 mảnh giấy. Hỏi người ta đếm đúng hay sai?
7. Ước, Ước chung lớn nhất
Phần này giúp học sinh hiểu và tìm các ước của một số, đặc biệt là ước chung lớn nhất (ƯCLN) của các số. Đây là khái niệm quan trọng trong đại số và là cơ sở để giải quyết các bài toán chia hết, tìm tỉ lệ.
+ Nhận biết một số thuộc ước chung của hai hay nhiều số
Ví dụ: Số 12 có là ước chung của 24 và 40 không? Vì sao?
+ Tìm ước chung lớn nhất của các số cho trước
Ví dụ: Tìm ước chung lớn nhất của 12 và 18?
+ Viết tập hợp ước chung của hai hay nhiều số
Ví dụ: Viết tập hợp sau: ƯC(15;27)
+ Chứng minh hai hay nhiều số là các số nguyên tố cùng nhau
Ví dụ: Chứng minh rằng: Với mọi số tự nhiên n, các số sau là các số nguyên tố cùng nhau:
a) n + 1; n + 2
b) 3n + 10; 3n + 9
+ Toán có lời văn
Ví dụ: Lớp 6A có 18 bạn nam và 24 bạn nữ. Trong một buổi sinh hoạt lớp, bạn lớp trưởng dự kiến chia các bạn thành từng nhóm sao cho số bạn nam trong mỗi nhóm đều bằng nhau và số bạn nữ cũng vậy. Hỏi lớp có thể chia được nhiều nhất bao nhiêu nhóm? Khi đó mỗi nhóm có bao nhiêu bạn nam, bao nhiêu bạn nữ?
8. Bội, Bội chung nhỏ nhất
Bài tập về bội và bội chung nhỏ nhất (BCNN) giúp học sinh hiểu cách tìm bội chung nhỏ nhất của các số cho trước, áp dụng vào các bài toán thực tế.
+ Tìm bội chung nhỏ nhất của các số cho trước
Ví dụ: Tìm bội chung nhỏ nhất của 24 và 10.
+ Viết tập hợp bội chung của hai hay nhiều số
Ví dụ: Tìm các bội chung có hai chữ số của 6 và 8.
+ Tìm số chưa biết
Ví dụ: Tìm số tự nhiên x biết x chia hết cho 4; 7; 8 và x nhỏ nhất.
+ Toán có lời văn
Ví dụ: Học sinh của một trường học khi xếp hàng 3, hàng 4, hàng 7, hàng 9 đều vừa đủ hàng. Tìm số học sinh của trường, cho biết số học sinh của trường trong khoảng từ 1600 đến 2000 học sinh.
9. Cộng, trừ trong tập hợp các số nguyên
Trong phần này, học sinh sẽ thực hành các phép toán cộng, trừ với các số nguyên. Đồng thời, học sinh cũng sẽ giải quyết các bài toán có lời văn liên quan đến số nguyên, rèn luyện kỹ năng phân tích và tư duy logic.
+ Tính giá trị của biểu thức
Ví dụ: Tính giá trị của biểu thức sau:
a) 2763 + 152
b) (-7) + (-14)
c) (-35) + (-9)
+ Tìm x ∈ Z
Ví dụ:
Tìm x ∈ Z:
a) -7 < x < -1
b) -3 < x < 3
+ Tìm tổng của các số nguyên thỏa mãn điều kiện cho trước
Ví dụ: Tìm tổng của tất cả các số nguyên thỏa mãn:
a) – 4 < x < 3
b) -5 < x < 5
c) -10 < x < 6
+ Toán có lời văn
Ví dụ: Hai đoàn tàu hỏa xuất phát cùng một lúc từ Huế đi về hai phía Hà Nội và thành phố Hồ Chí Minh. Ta quy ước chiều từ Huế đến Hà Nội là chiều dương, chiều ngược lại từ Huế đến thành phố Hồ Chí Minh là chiều âm. Hỏi sau 1h hai đoàn tàu cách nhau bao nhiêu kilomet nếu vận tốc của chúng lần lượt là:
a) 45km/h và 40km/h
b) 45km/h và – 40km/h.
+ Dạng toán tổng hợp
Ví dụ: Cho a, b là số nguyên. Chứng minh:
a) Nếu b > 0 thì a + b > a
b) Nếu b < 0 thì a + b < a
10. Toán nâng cao
Đây là phần dành cho các bài toán có mức độ khó hơn, giúp học sinh thử thách khả năng tư duy, tính toán và chứng minh. Các bài toán nâng cao này không chỉ giúp rèn luyện kỹ năng toán học mà còn phát triển tư duy phản biện của học sinh.
Ví dụ 1: Chứng minh: A = 21 + 22 + 23 + 24 + …. + 22010 chia hết cho 3 và 7.
Ví dụ 2: So sánh A = 2009.2011 và B = 20102
Ví dụ 3: Tìm số tự nhiên x, biết 2x.4 = 128
Ví dụ 4: Số sau có phải là số chính phương không?
A = 3 + 32 + 33 + … + 320
Ví dụ 5: Tìm chữ số tận cùng của các số sau:
a) 21000
b) 4161
Ví dụ 6: Tìm số tự nhiên n sao cho n + 3 chia hết cho n − 1.
II. Phần hình học
Ở phần Hình học lớp 6, học sinh sẽ làm quen với khái niệm về độ dài đoạn thẳng trong hình học, từ đó áp dụng vào các bài toán tìm độ dài đoạn thẳng và chứng minh các điểm trên cùng một đoạn thẳng. Phần này giúp học sinh phát triển khả năng làm việc với các đối tượng hình học cơ bản và hiểu được các tính chất cơ bản của các đoạn thẳng.
Ví dụ: Cho điểm O thuộc đường thẳng xy. Trên tia Ox lấy hai điểm M, N sao cho OM = 2cm; ON = 7cm. Trên tia Oy lấy điểm P sao cho OP = 3cm.
a) Tính độ dài đoạn thẳng MN, NP
b) Chứng minh rằng M là trung điểm của đoạn thẳng NP.
c) Gọi I là trung điểm của đoạn thẳng MN. Tính MI, OI.
Hi vọng rằng các dạng bài tập Toán lớp 6 học kì 1 thường gặp nhất trong đề thi ở trên đã giúp các em nắm vững kiến thức cơ bản, từ đó tự tin hơn trong việc giải quyết các bài toán và bài kiểm tra sắp tới.
Các dạng bài tập Toán lớp 6 học kì 1 ở trên đều có sẵn trong cuốn Làm chủ kiến thức Toán lớp 6 bằng sơ đồ tư duy – Tập 1 của TKbooks kèm theo đáp án và giải thích chi tiết. Các em hãy đặt mua ngay cuốn sách này để học tốt môn Toán hơn nhé!
Link đọc thử sách: https://drive.google.com/file/d/15hxIEGdjgolqg9gMVAMIJ-rjhX0lHILs/view
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 6 hàng đầu tại Việt Nam!


