Chưa có sản phẩm trong giỏ hàng.
Cách chứng minh tam giác cân lớp 9 kèm ví dụ cực chi tiết
Trong toán học, tam giác cân là một khái niệm cơ bản nhưng vô cùng quan trọng. Việc chứng minh tam giác cân giúp học sinh hiểu rõ hơn về các tính chất hình học và cách áp dụng vào giải các bài toán.
Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu cách chứng minh một tam giác là tam giác cân thông qua các phương pháp khác nhau.
Mời các em tham khảo!
I. Lý thuyết về tam giác cân
1. Khái niệm tam giác cân
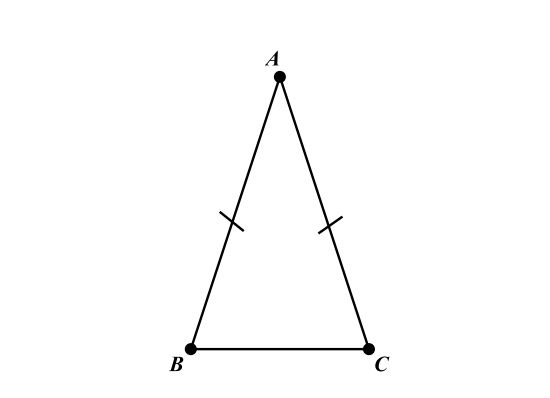
Tam giác cân là tam giác có hai cạnh bằng nhau và hai góc đối diện với hai cạnh đó cũng bằng nhau. Điều này có nghĩa là nếu tam giác ABC là tam giác cân tại A, thì AB = AC và góc B = góc C.
Hai cạnh bằng nhau của tam giác cân được gọi là hai cạnh bên, cạnh còn lại là cạnh đáy.
2. Tính chất của tam giác cân
- Tam giác cân có hai góc ở đáy bằng nhau.
- Nếu một tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.
II. Phương pháp chứng minh tam giác cân
1. Chứng minh bằng cách sử dụng định nghĩa
Để chứng minh một tam giác là tam giác cân, bạn có thể sử dụng định nghĩa của tam giác cân. Cụ thể, tam giác cân là tam giác có hai cạnh bằng nhau. Khi đó, hai góc đối diện với hai cạnh này cũng bằng nhau.
Ví dụ: Cho tam giác ABC, nếu biết rằng AB = AC, ta có thể kết luận rằng tam giác ABC là tam giác cân tại A.
+ Các bước chứng minh cụ thể:
- Xác định các cạnh bằng nhau:
Trước tiên, bạn cần xác định hai cạnh bằng nhau trong tam giác. Trong ví dụ này, giả sử chúng ta biết rằng AB = AC.
- Sử dụng định nghĩa của tam giác cân:
Theo định nghĩa, nếu một tam giác có hai cạnh bằng nhau, thì tam giác đó là tam giác cân. Do đó, với giả thiết AB = AC, ta có thể kết luận rằng tam giác ABC là tam giác cân tại A.
- Chứng minh các góc bằng nhau:
Trong một tam giác cân, hai góc đối diện với hai cạnh bằng nhau cũng bằng nhau. Do đó, chúng ta có thể suy ra rằng góc B = góc C.
+ Chứng minh chi tiết:
Giả sử tam giác ABC có AB = AC. Chúng ta cần chứng minh rằng tam giác ABC là tam giác cân tại A và góc B = góc C.
Bước 1: Giả thiết AB = AC.
Bước 2: Theo định nghĩa của tam giác cân, nếu AB = AC thì tam giác ABC là tam giác cân tại A.
Bước 3: Do tam giác ABC là tam giác cân tại A, nên hai góc đối diện với hai cạnh bằng nhau sẽ bằng nhau. Tức là góc B = góc C.
+ Ví dụ minh họa:
Giả sử trong một bài toán, bạn được cho tam giác PQR và biết rằng PQ = PR. Để chứng minh tam giác PQR là tam giác cân tại P, bạn có thể thực hiện các bước sau:
Xác định các cạnh bằng nhau: PQ = PR (đã cho).
Sử dụng định nghĩa: Theo định nghĩa của tam giác cân, nếu PQ = PR thì tam giác PQR là tam giác cân tại P.
Chứng minh các góc bằng nhau: Trong tam giác PQR, góc Q = góc R (vì đối diện với hai cạnh bằng nhau).
Như vậy, chúng ta đã chứng minh được tam giác PQR là tam giác cân tại P bằng cách sử dụng định nghĩa của tam giác cân.
2. Chứng minh bằng cách sử dụng định lý
Một cách khác để chứng minh tam giác cân là sử dụng các định lý hình học. Một định lý phổ biến là định lý về đường trung trực.
+ Định lý về đường trung trực:
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó. Một đặc điểm quan trọng của đường trung trực là nó sẽ chia đoạn thẳng thành hai phần bằng nhau và bất kỳ điểm nào nằm trên đường trung trực cũng sẽ cách đều hai đầu mút của đoạn thẳng đó.
Ví dụ: Chứng minh tam giác ABC là tam giác cân nếu đường trung trực của cạnh BC chia tam giác thành hai phần bằng nhau.
+ Chứng minh chi tiết:
Giả thiết: Đường trung trực của BC cắt BC tại D, và D là trung điểm của BC. Do đó, DB = DC.
Lập luận: Đường trung trực của BC là đường thẳng vuông góc với BC tại D, nghĩa là góc BDC = 90°.
Chứng minh: Xét hai tam giác ABD và ACD:
- AB = AC (giả thiết tam giác cân cần chứng minh).
- AD là cạnh chung.
- DB = DC (vì D là trung điểm của BC).
Theo định lý ba cạnh bằng nhau (SSS), ta có tam giác ABD = tam giác ACD.
Kết luận: Do hai tam giác ABD và ACD bằng nhau, suy ra góc BAD = góc CAD và cạnh AB = AC. Vậy tam giác ABC là tam giác cân tại A.
3. Chứng minh bằng cách sử dụng tính chất góc
Một cách khác để chứng minh tam giác cân là sử dụng tính chất các góc của tam giác.
+ Tính chất góc của tam giác cân:
Trong một tam giác cân, hai góc đối diện với hai cạnh bằng nhau cũng bằng nhau.
Ví dụ: Chứng minh tam giác ABC là tam giác cân nếu biết rằng góc B = góc C.
+ Chứng minh chi tiết:
Giả thiết: Góc B = góc C.
Lập luận: Theo tính chất tổng các góc trong tam giác, ta có:
Góc A + góc B + góc C = 180°.
Vì góc B = góc C, ta có thể gọi chung là góc B. Do đó, 2 góc B + góc A = 180°.
Chứng minh: Từ đó, ta có:
2 góc B = 180° – góc A.
Góc B = (180° – góc A) / 2.
Kết luận: Vì góc B = góc C và chúng đối diện với hai cạnh AB và AC, nên AB = AC. Vậy tam giác ABC là tam giác cân tại A.
+ Ví dụ minh họa:
Giả sử trong một bài toán, bạn được cho tam giác XYZ và biết rằng góc X = góc Y. Để chứng minh tam giác XYZ là tam giác cân tại Z, bạn có thể thực hiện các bước sau:
Giả thiết: Góc X = góc Y.
Lập luận: Tổng các góc trong tam giác là 180°. Vì góc X = góc Y, ta có:
- 2 góc X + góc Z = 180°.
- 2 góc X = 180° – góc Z.
- Góc X = (180° – góc Z) / 2.
Chứng minh: Vì góc X = góc Y và chúng đối diện với hai cạnh ZX và ZY, nên ZX = ZY.
Kết luận: Vậy tam giác XYZ là tam giác cân tại Z.
Việc chứng minh tam giác cân không chỉ giúp các em học sinh nắm vững kiến thức hình học mà còn rèn luyện kỹ năng tư duy logic và áp dụng lý thuyết vào thực tiễn. Hy vọng qua bài viết này, các em sẽ có thêm nhiều cách tiếp cận để chứng minh một tam giác là tam giác cân. Hãy thực hành nhiều bài tập để thành thạo hơn nhé!
Đừng quên tham khảo thêm 2 cuốn Làm chủ kiến thức Toán 9 ôn thi vào 10 phần Đại số và Hình học để biết cách giải tất cả các bài toán trong chương trình lớp 9 nhé!
Link đọc thử phần Đại số: https://drive.google.com/file/d/1uaOJCek1Mpmm-UbFU3hEIVzQ0P6PPaoC/view
Link đọc thử phần Hình học: https://drive.google.com/file/d/162Yv0A_lC8XmgSN_AjwxVuKPWpbVVkJj/view
Nếu các em có bất kỳ thắc mắc nào, hãy để lại bình luận dưới bài viết để được giải đáp nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 9 hàng đầu tại Việt Nam!


