Các cách chứng minh tia phân giác lớp 9 kèm ví dụ cực chi tiết
Trong bài viết này, chúng ta sẽ cùng tìm hiểu các cách chứng minh tia phân giác thường gặp trong chương trình Toán lớp 9 cũng như khái niệm và tính chất của tia phân giác của góc, tam giác.
Mời các em tham khảo!
>>> Xem thêm:
Cách chứng minh tứ giác nội tiếp lớp 9 kèm bài tập và lời giải cực chi tiết
I. Khái niệm và tính chất của tia phân giác
1. Tia phân giác của một góc
a. Khái niệm tia phân giác của một góc
Tia phân giác của một góc là tia nằm giữa hai cạnh, và chia góc đã cho thành hai góc bằng nhau.
Trong hình vẽ, tia Oy là tia phân giác của góc xOz, ta có góc ∠xOy = góc ∠yOz = ½ góc ∠xOz.
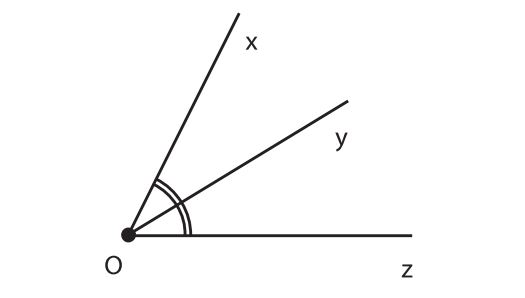
b. Tính chất tia phân giác của một góc
+ Tính chất chia đôi góc
Tia phân giác của góc ∠ABC chia góc này thành hai góc bằng nhau:
∠ABD = ∠DBC
Trong đó BD là tia phân giác của góc ∠ABC.
+ Tính chất khoảng cách
Bất kỳ điểm nào nằm trên tia phân giác của một góc đều cách đều hai cạnh của góc đó. Nếu điểm P nằm trên tia phân giác của góc ∠ABC thì khoảng cách từ P đến hai cạnh AB và BC là bằng nhau:
d(P,AB) = d(P,BC)
c. Cách vẽ tia phân giác
- Chia số đo góc thành hai phần bằng nhau.
- Vẽ tia phân giác nằm giữa hai cạnh của góc, sao cho góc tạo bởi một cạnh và tia phân giác bằng nửa số đo của góc đã cho.
2. Đường phân giác của tam giác
a. Khái niệm đường phân giác của tam giác
Đường phân giác của tam giác là đoạn thẳng kẻ từ một đỉnh của tam giác đến cạnh đối diện, chia góc tại đỉnh đó thành hai góc bằng nhau. Mỗi tam giác có ba đường phân giác, và điểm giao nhau của ba đường phân giác này gọi là trọng tâm của tam giác.
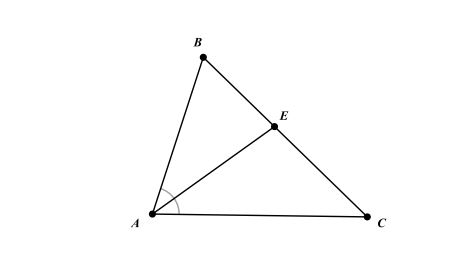
b. Tính chất của đường phân giác của tam giác
+ Tính chất chia cạnh đối diện:
Đường phân giác của một góc trong tam giác chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của góc đó. Nếu đường phân giác của góc A trong tam giác ABC cắt cạnh BC tại điểm D, thì ta có:
BD/DC = AB/AC
+ Đường tròn nội tiếp:
Ba đường phân giác trong tam giác giao nhau tại một điểm duy nhất, gọi là tâm của đường tròn nội tiếp tam giác. Điểm này cách đều ba cạnh của tam giác và là tâm của đường tròn nội tiếp tam giác.
+ Độ dài đường phân giác:
Độ dài của đường phân giác trong tam giác có thể được tính bằng công thức:
𝑙𝑎 = [2bc/(b + c)].cos(A/2)
Với a, b, c là độ dài các cạnh của tam giác, và A là góc đối diện với cạnh a.
Lưu ý: Định lý trên vẫn đúng cho trường hợp đường phân giác ngoài của tam giác.
II. Các cách chứng minh tia phân giác lớp 9
1. Chứng minh bằng định nghĩa tia phân giác
- Tia phân giác của một góc là tia nằm trong góc đó và chia góc đó thành hai góc bằng nhau.
- Để chứng minh một tia là tia phân giác của góc, ta có thể sử dụng định nghĩa này.
Giả sử cần chứng minh tia Oz là tia phân giác của góc AOB:
+ Cách chứng minh
- Xác định góc AOz và góc zOB.
- Chứng minh rằng ∠AOz =∠zOB.
Ví dụ:
Cho ∠AOB= 60°, tia Oz chia góc ∠AOB thành hai góc ∠AOz và ∠zOB. Nếu ∠AOz = 30° và ∠zOB = 30° thì Oz là tia phân giác của ∠AOB.
2. Chứng minh bằng tam giác cân
- Nếu một điểm nằm trên tia phân giác của một góc thì điểm đó cách đều hai cạnh của góc.
Giả sử cần chứng minh tia Oz là tia phân giác của góc AOB:
+ Cách chứng minh:
- Xác định điểm P bất kỳ trên tia Oz.
- Chứng minh rằng khoảng cách từ P đến OA bằng khoảng cách từ P đến OB.
Ví dụ:
Chọn điểm P trên tia Oz.
Dựng các đoạn vuông góc từ P đến OA và OB, gọi lần lượt là PH và PK. Nếu PH = PK thì tia Oz là tia phân giác của ∠AOB.
3. Chứng minh bằng tính chất đường tròn
- Nếu điểm nằm trên đường tròn nội tiếp tam giác và cách đều các cạnh của tam giác, thì điểm đó là tâm của đường tròn nội tiếp tam giác và các đoạn nối từ điểm đó đến các đỉnh của tam giác là các tia phân giác.
Giả sử cần chứng minh tia Oz là tia phân giác của góc ∠AOB:
+ Cách chứng minh:
- Xác định tam giác AOB và đường tròn nội tiếp tam giác này.
- Chứng minh rằng Oz đi qua tâm của đường tròn nội tiếp và tạo thành các đoạn cách đều từ điểm đó đến các cạnh của tam giác.
Ví dụ:
Dựng đường tròn nội tiếp tam giác AOB với tâm I.
Nếu tia Oz đi qua I và chia góc AOB thành hai góc bằng nhau, thì Oz là tia phân giác của ∠AOB.
4. Chứng minh bằng các tính chất của tam giác đồng dạng
- Nếu hai tam giác đồng dạng với nhau thì các cặp góc tương ứng bằng nhau.
Giả sử cần chứng minh tia Oz là tia phân giác của góc AOB:
+ Cách chứng minh:
Dựng các tam giác có chứa tia phân giác cần chứng minh.
Chứng minh rằng các tam giác này đồng dạng và các góc tương ứng bằng nhau.
Ví dụ:
- Dựng tam giác AOP và BOP với điểm P nằm trên Oz.
- Nếu tam giác AOP và BOP đồng dạng, thì ∠AOz =∠zOB, và tia Oz là tia phân giác của ∠AOB.
Các cách chứng minh tia phân giác không chỉ giúp học sinh nắm vững kiến thức mà còn rèn luyện kỹ năng tư duy logic và khả năng áp dụng các định lý, định nghĩa vào giải toán. Việc nắm chắc các phương pháp chứng minh tia phân giác sẽ là nền tảng vững chắc cho học sinh lớp 9 trong việc ôn thi vào lớp 10 và các kỳ thi quan trọng khác. Hy vọng bài viết này sẽ là tài liệu hữu ích cho các em học sinh trong quá trình học tập và ôn luyện.
Đừng quên tham khảo thêm 2 cuốn Làm chủ kiến thức Toán 9 ôn thi vào 10 phần Đại số và Hình học để biết cách giải tất cả các bài toán trong chương trình lớp 9 nhé!
Link đọc thử phần Đại số: https://drive.google.com/file/d/1uaOJCek1Mpmm-UbFU3hEIVzQ0P6PPaoC/view
Link đọc thử phần Hình học: https://drive.google.com/file/d/162Yv0A_lC8XmgSN_AjwxVuKPWpbVVkJj/view
Nếu các em có bất kỳ thắc mắc nào, hãy để lại bình luận dưới bài viết để được giải đáp nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 9 hàng đầu tại Việt Nam!