Chưa có sản phẩm trong giỏ hàng.
Cách chứng minh tứ giác nội tiếp lớp 9 kèm bài tập và lời giải cực chi tiết
Trong chương trình Toán lớp 9, việc chứng minh tứ giác nội tiếp là một phần quan trọng giúp học sinh nắm vững kiến thức về hình học và phát triển tư duy logic.
Bài viết này sẽ hướng dẫn các em cách chứng minh tứ giác nội tiếp một cách chi tiết và dễ hiểu thông qua phần lý thuyết, cách chứng minh tứ giác nội tiếp cũng như các bài tập kèm lời giải cực chi tiết.
Mời các em tham khảo!
I. Lý thuyết về tứ giác nội tiếp
1. Khái niệm tứ giác nội tiếp
Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp.
a. Tính chất
- Định lý 1: Một tứ giác được gọi là nội tiếp khi và chỉ khi tổng số đo hai góc đối bằng 180°.
- Định lý 2: Nếu một tứ giác có hai góc ở cùng 1 phía so với 1 cạnh, và cùng nhìn cạnh đó với một góc α thì tứ giác đó là tứ giác nội tiếp.
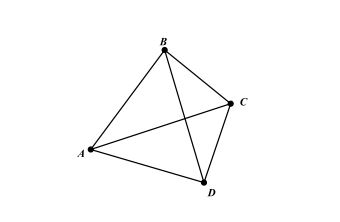
Ví dụ tứ giác ABCD như hình có góc ABD = góc ACD thì tứ giác này là tứ giác nội tiếp.
b. Cách chứng minh tứ giác nội tiếp
+ Như vậy để chứng minh một tứ giác là nội tiếp ta cần chứng minh tứ giác đó có tổng hai góc đối bằng 180°.
+ Nếu ta có một tứ giác là nội tiếp, thì ta suy ra được tổng số đo hai góc đối bằng 180°.
c. Ví dụ
Trong hình vẽ tứ giác ABCD là tứ giác nội tiếp.
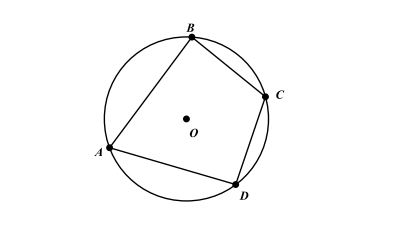
Góc BAD và BCD là hai góc đối nhau nên ta có thể BAD + BCD = 180°.
II. Các bài toán chứng minh tứ giác nội tiếp lớp 9
Bài 1:
Cho tam giác ABC nội tiếp đường tròn (O). Đường thẳng song song với tiếp tuyến tại C của đường tròn (O), cắt các cạnh AC, BC lần lượt ở D, E. Chứng minh rằng tứ giác ABED nội tiếp.
Giải:
Gọi Cx là tia tiếp tuyến của đường tròn (O) (tia Cx nằm trên nửa mặt phẳng bờ AC không chứa B). Ta có góc ACx = góc ABC, mà góc ACx = góc EDC nên góc ABC = góc EDC.
Vậy tứ giác ABED nội tiếp.
Bài 2:
Cho tam giác ABC nội tiếp đường tròn (O). Vẽ dây DE vuông góc với OA cắt các cạnh AB, AC lần lượt S, K .
Chứng minh rằng: tứ giác BCKS nội tiếp.
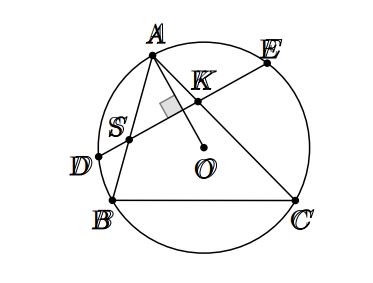
Giải:
OA ⊥ DE (gt) => góc xAC = góc AED
⇒ AD AE
Góc BSK = (số đo cung BCE + số đo cung AD)/2 (góc có 2 đỉnh ở bên trong đường tròn)
Góc BSK = số đo cung AB/2 (góc nội tiếp).
Do đó: Góc BSK + góc BCK = (số đo cung BCE + số đo cung AD + số đo cung AB)/2
= (số đo cung BCE + số đo cung AE + số đo cung AB)/2 = 360°/2 = 180°
⇒ Tứ giác nội BCKS nội tiếp.
Bài 3:
Cho tam giác nhọn ABC. Đường tròn đường kính BC cắt AB và AC theo thứ tự tại D và E. Gọi H là giao điểm của BE và CD,tia AH cắt BC tại F. Số tứ giác nội tiếp được đường tròn có trong hình vẽ là bao nhiêu?
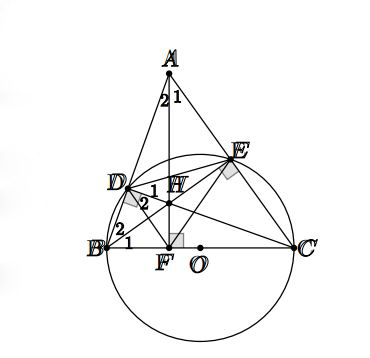
Giải:
Ta có tam giác BDC vuông tại D và tam giác BEC vuông tại E vì hai tam giác này nội tiếp nửa đường tròn (O) đường kính BC.
BE và CD là hai đường cao của ABC nên H là trực tâm của tam giác này.
⇒ AH ⊥ BC tại F (vì AH là đường cao thứ ba).
Từ đó ta có:
– Ba tứ giác AEDH; BDHF; CEHF nội tiếp được vì có hai góc đối diện bù nhau.
– Ba tứ giác AEFB; BDEC; ADFC nội tiếp được vì có hai đỉnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc 90°.
Vậy trong hình vẽ có tất cả 6 tứ giác nội tiếp được đường tròn.
Bài 4:
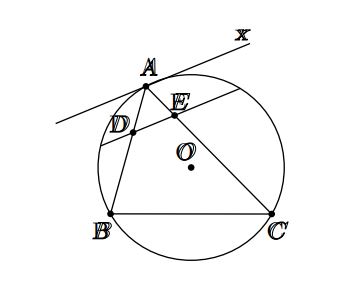
Cho tam giác ABC nội tiếp đường tròn (O). Vẽ Ax là tiếp tuyến của đường tròn (O). Đường thẳng song song với A cắt các cạnh AB, AC lần lượt tại D, E.
Chứng minh rằng tứ giác BCED nội tiếp.
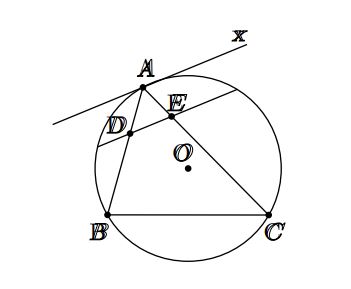
Giải:
Ta có Ax // DE (giả thiết)
⇒ Góc xAC = góc AED (hệ quả của góc tạo bởi tia tiếp tuyến dây cung)
Do đó: góc AED = góc DBC
Suy ra tứ giác BCED nội tiếp.
Bài 5:
Cho tam giác ABC cân tại A, nội tiếp trong đường tròn (O) đường kính là AI . Gọi E là trung điểm AB và K là trung điểm của OI.
a) Chứng minh tam giác EKB là tam giác cân.
b) Chứng minh tứ giác AEKC là một tứ giác nội tiếp được.
Giải:
a) Gọi H là trung điểm của đoạn thẳng BE.
Ta có: E là trung điểm AB, AB không qua O (gt). Mà góc ABI = 90° (góc nội tiếp chắn nửa đường tròn).
Vì OE ⊥ AB, BI ⊥ AB (góc ABI = 90°) ⇒ OE // BI.
Do đó tứ giác BEOI là hình thang.
Mà H, K lần lượt là trung điểm các cạnh BE, OI nên HK // OE.
Ta có: HK // OE, OE ⊥ AB => HK ⊥ AB
Tam giác EKB có HK vừa là đường cao vừa là đường trung tuyến => tam giác EKB cân tại K.
b) OB = OC (= R) và AB = AC (gt)
⇒ O và A thuộc đường trung trực của đoạn thẳng BC.
⇒ OA là đường trung trực của đoạn thẳng BC.
Mà K ∈ OA nên KB = KC
Xét tam giác KBA và tam giác ICA có: AB = AC (gt)
KB = KC; AK là cạnh chung
Do đó: tam giác KBA = tam giác RCA (c.c.c)
⇒ Góc KBA = góc KCA => góc KBA = góc KEB (tam giác EKB cân tại K).
Do đó: góc KEB = góc KCA => Tứ giác AEKC nội tiếp được.
Việc nắm vững cách chứng minh tứ giác nội tiếp lớp 9 không chỉ giúp các em học tốt môn Toán mà còn giúp các em đạt điểm cao hơn trong kỳ thi tuyển sinh vào 10 sắp tới.
Hy vọng qua bài viết này, các em sẽ có thể tự tin hơn khi đối mặt với các bài toán liên quan đến tứ giác nội tiếp.
Đừng quên tham khảo thêm 2 cuốn Làm chủ kiến thức Toán 9 ôn thi vào 10 phần Đại số và Hình học để biết cách giải tất cả các bài toán trong chương trình lớp 9 nhé!
Link đọc thử phần Đại số: https://drive.google.com/file/d/1uaOJCek1Mpmm-UbFU3hEIVzQ0P6PPaoC/view
Link đọc thử phần Hình học: https://drive.google.com/file/d/162Yv0A_lC8XmgSN_AjwxVuKPWpbVVkJj/view
Nếu các em có bất kỳ thắc mắc nào, hãy để lại bình luận dưới bài viết để được giải đáp nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 9 hàng đầu tại Việt Nam!


