Bài tập tam giác đồng dạng lớp 8 có đáp án cực chi tiết

Bài viết Bài tập tam giác đồng dạng lớp 8 có đáp án này sẽ trình bày các dạng bài tập đa dạng, từ cơ bản đến nâng cao, kèm theo lời giải chi tiết và cách tiếp cận từng bài toán về tam giác đồng dạng, nhằm mục đích giúp các em có thể áp dụng những kỹ năng này để giải quyết các bài tập tương tự.

Hãy cùng TKbooks khám phá và làm chủ các bài toán về tam giác đồng dạng dưới đây để tự tin hơn trong học tập và các kỳ thi sắp tới.

>>> Xem trước lý thuyết về tam giác đồng dạng để ôn tập và làm bài tập tốt hơn các em nhé!

Dạng 1: Chứng minh hai tam giác đồng dạng

1. Phương pháp giải

Dựa vào định nghĩa, tính chất hoặc định lý để chứng minh các tam giác đồng dạng.

2. Các ví dụ

Ví dụ 1: Tìm các cặp tam giác đồng dạng trong các tam giác dưới đây:

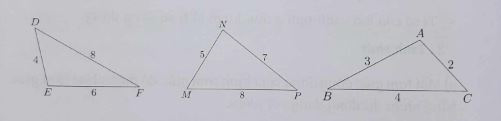
+ Lời giải

Xét tam giác △ABC và △DEF, ta có:

AB/DE = 2/4 = ½; AC/È = 3/6 = ½; BC/DF = 4/8 = ½.

Suy ra AB/DE = AC/EF = BC/DF = ½.

Vậy △ABC ∼ △DEF.

Ví dụ 2: Cho tam giác ABC. Hãy vẽ tam giác đồng dạng với tam giác ABC theo tỉ số đồng dạng:

a) k = 2/3.

b) k = 4/3.

+ Lời giải

a) Giả sử ta vẽ được △AMN ∼ △ABC theo tỉ số k = 2/3, khi đó AM/AB = 2/3 = k.

Từ đó suy ra cách vẽ gồm hai bước sau:

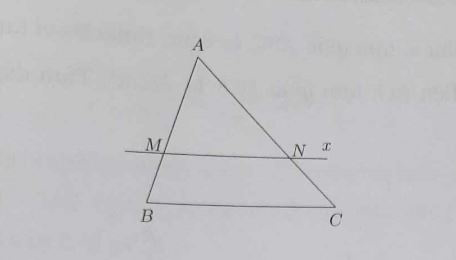
Bước 1. Trên cạnh AB lấy điểm M sao cho AM/AB = 2/3.

Bước 2. Kẻ Mx // BC cắt AC ở N.

Ta có △AMN ∼ △ABC theo tỉ số k = 2/3.

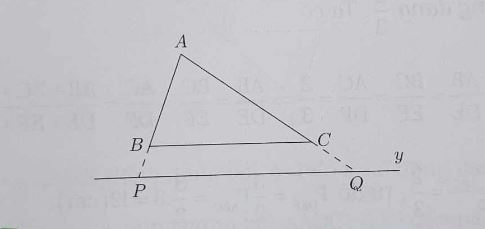
b) Giả sử đã vẽ được △APQ ∼ △ABC theo tỉ số k = 4/3, khi đó AP/AB = 4/3 = k.

Từ đó suy ra cách vẽ gồm hai bước sau:

• Bước 1. Trên tia AB lấy điểm P sao cho AP/AB = 4/3.
• Bước 2. Kẻ Py // BC cắt tia AC ở Q. Ta có △APQ ∼ △ABC.

Dạng 2: Tính độ dài cạnh, tỉ số đồng dạng thông qua các tam giác đồng dạng

1. Phương pháp giải

• Sử dụng định nghĩa và tính chất hai tam giác bằng nhau.
• Áp dụng tính chất dãy tỉ số bằng nhau.

2. Các ví dụ

Ví dụ 1: Tam giác ABC đồng dạng tam giác DEF theo tỉ số đồng dạng là 2/3.

a) Biết chu vi tam giác ABC là 8cm, tính chu vi tam giác DEF.

b) Biết diện tích tam giác DEF là 27cm. Tính diện tích tam giác ABC.

+ Lời giải

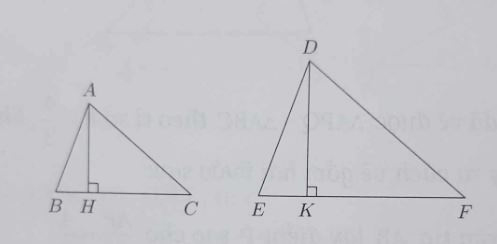
a) Gọi P là chu vi. Tam giác ABC đồng dạng với tam giác DEF theo tỉ số đồng dạng 2/3. Ta có:

AB/DE = BC/EF = AC/DF = 2/3 => AB/DE =BC/EF = AC/DF = (AB + BC + AC)/(DE + EF + DF) = 2/3.

⇒ Chu vi tam giác ABC/ Chu vi tam giác DEF = 2/3, từ đó chu vi tam giác DEF = 3/2 chu vi tam giác ABC = 3/2.8 = 12 (cm).

b) Tam giác DEK đồng dạng với tam giác ABH (do góc DEK = góc ABH, góc DKE = góc AHB).

Suy ra AB/DE = AH/DK. Mà AB/DE = 2/3 => AH/DK = 2/3.

Ta có:

Tam giác ABC/tam giác DEF = (½.AH.BC)/(1/2.DK.EF) = AH/DK. BC/EF – 2/3.2/3 = 4/9.

Suy ra diện tích tam giác ABC = 4/9 diện tích tam giác DEF = 4/9.27 = 12 (cm²)

Nhận xét: Nếu tam giác ABC đồng dạng với tam giác DEF theo tỉ số đóng dạng k thì khi đó:

Chu vi tam giác ABC/chu vi tam giác DEF = k, diện tích tam giác ABC/diện tích tam giác DEF = k².

Ví dụ 2: Cho hình bình hành ABCD. Trên đường chéo AC lấy điểm E sao cho AC = 3AE. Qua E vẽ đường thẳng song song với CD, cắt AD và BC thứ tự ở M và N.

a) Tìm tam giác đồng dạng với tam giác ADC và tìm tỉ số đồng dạng.

b) Điểm E ở vị trí nào trên AC thì E là trung điểm của MN?

+ Lời giải

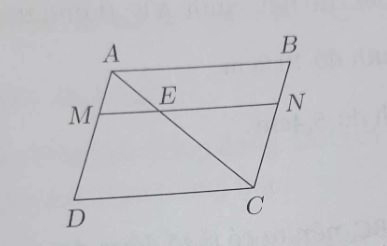
a) ME // DC => △AME đồng dạng với △ADC, tỉ số đồng dạng: AE/AC = 1/3.

△CBA = △ADC => △CBA đồng dạng với △ADC, tỉ số đồng dạng bằng 1.

EN // AB => △CNE đồng dạng với △CBA, do đó △CNE đồng dạng với △ADC, tỉ số đồng dạng CE/AC = 2/3.

b) Ta có CN // AM nên EM/EN = EA/EC.

Do đó ME = EN ó AE = EC ó E là trung điểm của AC.

Ví dụ 3: Tam giác ABC có cạnh BC = 10cm, CA = 14cm, AB = 6cm. Tam giác ABC đồng dạng với tam giác DEF có cạnh nhỏ nhất là 9cm. Tính các cạnh còn lại của tam giác DEF.

+ Lời giải

Ta có: △ABC đồng dạng với △DEF nên AB/DE = AC/DF = BC/EF.

△ABC có cạnh nhỏ nhất là cạnh AB = 6cm. Nên cạnh nhỏ nhất của △DEF là DE = 9cm.

Ta có

AB/DE = AC/DF = BC/EF = 6/9 = 14/DF = 10/EF.

Từ đó ta tính được: DF =21cm, EF = 15cm.

Ví dụ 4: Cho tam giác ABC có AB = 16,2cm, BC = 24,3cm, CA = 32,7cm. Tính độ dài các cạnh của tam giác A’B’C’ đồng dạng với tam giác đã cho nếu cạnh A’B’ tương ứng với cạnh AB và

a) Lớn hơn cạnh đó 10,8cm.

b) Bé hơn cạnh đó 5,4cm.

+ Lời giải

Vì △A’B’C’ đồng dạng với △ABC nên ta có tỉ số đồng dạng:

k = A’B’/AB = B’C’/BC = C’A’/CA hay A’B’/16,2 = B’C’/24,3 = C’A’ = 32,7.

a) Từ giả thiết cạnh A’B’ tương ứng với cạnh AB và lớn hơn cạnh đó 10,8cm nên A’B’ = 27cm, do đó:

27/16,2 = 5/3 = B’C’/24,3 = C’A’/32,7 ó B’C’ = 40,5 (cm), C’A’ = 54,5 (cm).

b) Từ giả thiết cạnh A’B’ tương ứng với cạnh AB và bé hơn cạnh đó 5,4cm nên A’B’ = 27cm , do đó:

10,8/16,2 = 2/3 = B’C’/24,3 = C’A’/32,7 ó B’C’ = 16,2 (cm), C’A’ = 21,8 (cm).

Dạng 3: Nhận biết hai tam giác đồng dạng theo trường hợp c.c.c và chứng minh tính chất hình học

+ Phương pháp giải

Để chứng minh hai tam giác đồng dạng, ta lập tỉ số các cạnh tương ứng của hai tam giác và chứng minh chúng bằng nhau.

+ Các ví dụ

Ví dụ 1: Tam giác ABC có BC = a, AC = b, AB = c và a² = bc. Chứng minh rằng tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC.

+ Lời giải

Gọi độ dài ba đường cao kẻ từ A, B, C của △ABC lần lượt là ha, hb, hc.

Gọi tam giác DEF là tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC.

Ta có: 1/2a.ha = 1/2b.hb = 1/2c.hc (cùng là diện tích △ABC).

Suy ra: (a.ha)/bc = (b.hb)/bc = (c.hc)/bc mà bc = a (giả thiết) nên:

(a.ha)/a² = hb/c = hc/b => ha/a = hb/c = hc/b.

Xét △ABC và △DEF ta có: AB/DE = AC/DF = BC/EF (vì ha/a = hb/c = hc/b) nên  △sABC ∼ △DEF(c.c.c).

Vậy tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC.

Ví dụ 2: Có thể khẳng định rằng hai tam giác có hai cặp cạnh bằng nhau, ba cặp góc bằng nhau thì hai tam giác bằng nhau hay không?

+ Lời giải

Không thể khẳng định như vậy. Ta xét hai trường hợp sau:

• TH1: Xét hai tam giác có độ dài các cạnh bằng: 8cm, 12cm, 18cm và 27cm, 18cm, 12cm.

Dễ dàng chứng minh được hai tam giác trên đồng dạng vì 8/12 = 12/18 = 18/27  nên suy ra chúng có hai cặp cạnh bằng nhau và ba cặp góc bằng nhau (vì hai tam giác đồng dạng), nhưng hiển nhiên chúng không bằng nhau.

• TH 2: Xét tam giác ABC có AB = 4cm, AC = 6cm, BC = 9cm. Diểm D nằm trên cạnh BC sao cho CD = 4cm.

Khi đó ta dễ dàng chứng minh được △ABC ∼ △DAC vì có góc C chung và AC/BC = DC/AC = 3/2. Nhưng hiển nhiên hai tam giác này không bằng nhau.

Ví dụ 3: Cho tam giác ABC và một điểm O nằm trong tam giác đó. Trên cạnh OA lấy điểm D sao cho OD = 2/3OA. Qua D vẽ các đường thẳng song song với AB, AC lần lượt cắt OB, OC tại E và F.

a) Chứng minh: △DEF ∼ △ABC

b) Tính độ dài DE, AB biết hiệu độ dài hai cạnh đó là 12cm.

c) Tính chu vi của △DEF, biết rằng tổng chu vi của △ABC và △DEF là 120cm.

+ Lời giải

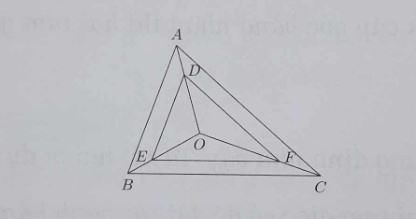
a) Ta có: DE // AB suy ra: △ODE ∼ △OAB => OD/OA = OE/OB = DE/AB = 2/3. (1)

Tương tự △ODF ∼ △OAC =>EF/BC = OF/OC = 2/3. (2)

Suy ra OE/OB = OF/OC = 2/3 => EF // BC (theo định lý Ta-lét đảo).

Do đó △OEF ∼ △OBC => EF/BC = OF/OC = 2/3 (3)

Từ (1), (2), (3) suy ra DF/AC = EF/BC = DE/AB = 2/3 => △DEF ∼ △ABC(c.c.c).

b) Ta có:

DE/AB = 2/3 => DE/2 = AB/3 mà AB – DE = 12. Theo tính chất dãy tỉ số bằng nhau ta có:

DE/2 = AB/3 = (AB – DE)/(3 – 2) = 12 => DE = 24(cm), AB = 36(cm).

c) Ta có tỉ số về chu vi đồng dạng △ABC ∼ △DEF theo tỉ số dồng dạng k = AB/DE = 3/2.

Do đó: Chu vi tam giác ABC/chi vu tam giác DEF = 3/2 => Chu vi tam giác ABC = 3/2 chu vi tam giác DEF. Mà theo giả thiết chu vi tam giác ABC + chu vi tam giác DEF = 120 suy ra:

3/2 chu vi tam giác BED + chu vi tam giác DEF = 120 => Chu vi tam giác DEF = 48(cm).

Dạng 4: Nhận biết hai tam giác đồng dạng theo trưởng hợp thứ hai cạnh – góc – cạnh và chứng minh tỉnh chất hình học

1. Phương pháp giải

Để chứng minh hai tam giác đồng dạng:

• Bước 1. Chọn ra hai góc bằng nhau, sắp xếp thứ tự hai cạnh tạo nên mỗi góc đó.
• Bước 2. Lập hai tỉ số, nếu chúng bằng nhau thì kết luận.

Từ định nghĩa tam giác đồng dạng suy ra tỉ số đông dạng, các góc tương ứng bằng nhau.

2. Các ví dụ

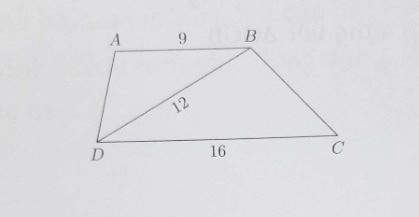
Ví dụ 1: Cho hình thang ABCD (AB // CD), biết AB = 9cm, BD = 12cm, DC = 16cm . Chứng minh △ABD ∼ △BDC.

+ Lời giải

Do hình thang ABCD có AB // DC nên góc ABD = góc BDC (so le trong).

Ta có

AB/BD = 9/12 = ¾, BD/DC = 12/16 = ¾ => AB/BD BD/DC = ¾.

Xét △ABD và △BDC có:

Góc ABD = góc BDC và AB/BD = BD/DC = ¾.

Từ đó suy ra: △ABD ∼ △BDC(c.g.c).

Ví dụ 2: Mệnh đề sau đúng hay sai: Hai tam giác có một cặp góc bằng nhau và hai cặp cạnh tỉ lệ thì đồng dạng với nhau.

+ Lời giải

Mệnh đề đã cho là sai. Dưới đây là hai trường hợp:

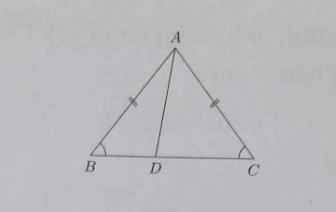
• TH 1: Xét △ABC cân ở A. D thuộc đáy BC nhưng không là trung điểm của BC. △ABD và △ACD có góc B = góc C, AD/AB = AD/AC nhưng chúng không đồng dạng.

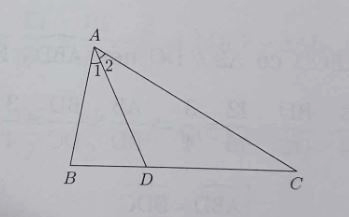
• TH 2: Xét △ABC có AB ≠ AC, phân giác AD. △ABD và △ACD có góc A1 = góc A2, BD/DC = AB/AC nhưng chúng không đồng dạng.

Ví dụ 3: Cho hình vuông ABCD, gọi O là giao điểm của hai đường chéo, lấy G trên BC, H trên CD sao cho GOH = 45°, gọi M là trung điểm của AB. Chứng minh rằng:

a) AHOD đồng dạng với AOGB.

b) MG // AH.

+ Lời giải

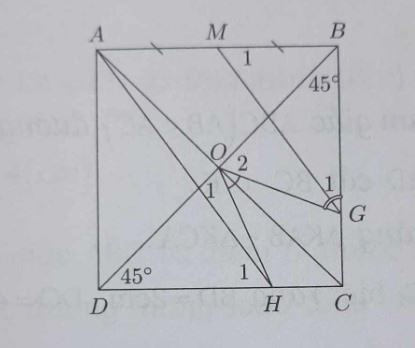
a) Ta có: Góc DBC = góc BDC = 45° . Mặt khác:

Góc O1 + góc O2 = 180°- 45° = 135°

Góc O2 + góc G1 = 180°- 45° = 135°

⇒ Góc O1 = góc G1 ⇒ △HOD ~ △OGB (g.g).

b) Theo câu a) △HOD ~ △OGB(gg), ta có HD/OB = OD/GB. Đặt MB = a, AD = 2a. Suy ra:

HD.GB = OB.OD = a√2.a√2 = 2a² = AD.BM

Từ đó HD/AD = BM/BG => △BMG ~ △DHA (c.g.c).

Suy ra M1 = H1, mà góc H1 = góc BAH (so le trong) => góc M1 = góc BAH (đồng vị).

Suy ra AH // MG.

Dạng 5: Nhận biết hai tam giác đồng dạng theo trường hợp thứ ba góc – góc và chứng minh tính chất hình học

1. Phương pháp giải

• Chứng minh hai tam giác có hai cặp góc bằng nhau.
• Áp dụng định nghĩa tam giác đồng dạng, lập tỉ số giữa các cạnh tương ứng.\

2. Các ví dụ

Ví dụ 1: Cho tam giác ABC (AB < AC), đường phân giác AD. Đường trung trực của AD cắt BC ở K.

a) Chứng minh rằng △KAB ~ △

b) Tính độ dài KD biết rằng BD = 2cm, DC = 4cm.

+ Lời giải

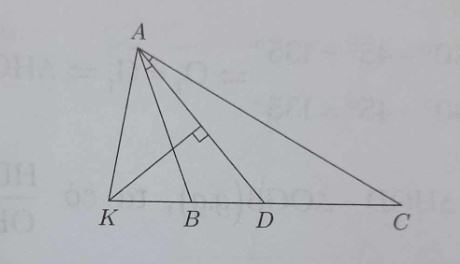
a) Do K thuộc đường trung trực của AD nên KA = KD . Khi đó △KAD cân tại K.

Suy ra: Góc KDA = góc KAD => góc DAC + góc DCA = góc KAB + góc BAD (KDA là góc ngoài tại đỉnh D của △DAC).

Mà góc DAC = góc BAD (AD là phân giác của △ABC) nên góc DCA = góc KAB.

Xét △KAB và △KCA ta có:

• Góc AKC là góc chung;
• Góc KAB = KCA (chứng minh trên).

Suy ra △KAB ~ △KCA(g.g).

b) Ta có:

KB/KA = AB/CA (vì △KAB ~ △KCA );

AB/AC = DC/CD (AD là phân giác của △ABC).

Suy ra KB/KA = ½, mà KA = KD (chứng minh trên) nên KD = 2KB.

Suy ra: KD = 2BD = 4(cm).

Ví dụ 2: Cho tam giác ABC và điểm O thuộc miền trong tam giác. Qua điểm O vẽ các đường thẳng song song với CA, CB, AB chúng lần lượt cắt các cạnh AB, BC, CA tại D, E, F. Chứng minh rằng AD/AB + BF/BC + CF/CA = 1.

+ Lời giải

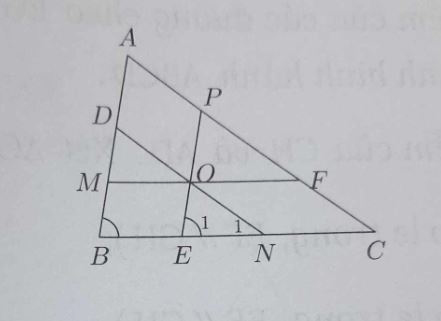
Ta có:

• DN // AC⇒ AD/AB = CN/CB. (1)
• Tứ giác OFCN là hình bình hành nên CF = CN. (2)
• OE // AB => Góc E1 = góc B và ON // AC => góc N1 = góc C
• △ABC ~ △OEN (g.g) => ON/AC = EN//BC. (3)

Từ (1), (2), (3) suy ra:

AD/AB + BE/BC + CF/CA = CN/Cb + BE/BC + ON/CA = BC/BC = 1 (dpcm).

Dạng 6: Phối hợp các trường hợp cạnh – góc – cạnh và góc – góc

Ví dụ 1: Một hình thang có bốn đỉnh thuộc bốn cạnh của một hình bình hành. Chứng minh rằng tồn tại một đường chéo của hình bình hành đi qua giao điểm hai đường chéo của hình thang.

+ Lời giải

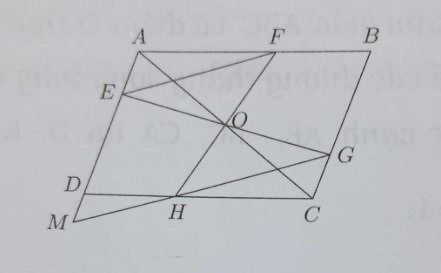
Gọi O là giao điểm của các đường chéo EG và FH của hình thang EFGH nội tiếp hình bình hành ABCD.

Gọi M là giao điểm của CH và AD. Xét △OEF và △OGH ta có:

• Góc OEF = góc OGH (so le trong, EF // GH);
• Góc OFE = góc OHG (so le trong, EF // GH).

Suy ra: △OEF ~ △OGH(g.g) ⇒ OE/OG = EF/GH. (1)

Xét △AEF và △CGH ta có:

• Góc A = góc C (ABCD là hình bình hành);
• Góc AEF = góc CGH (cùng bằng góc M).

Suy ra: △AEF ~ △CGH (g.g) => AE/CG = EF/GH. (2)

Từ (1), (2) suy ra:

AE/CG = OE/OG.

Xét △AOE và △COG ta có:

AE/CG = OE/OG;

Góc AEO = góc CGO (so le trong, AD // BC).

Suy ra: △AOE ~ △COG(c.g.c) => góc AOE = góc COG.

Mà góc AOE + góc AOG = 180° nên góc COG + góc AOG = 180°.

Suy ra A, O, C thẳng hàng. Vậy đường chéo AC của hình bình hành ABCD đi qua giao điểm hai đường chéo của hình thang EFGH.

Ví dụ 2: Cho tam giác ABC vuông tại A có điểm D nằm giữa A và C. Qua C dựng CE vuông góc với đường thẳng BD tại E. Chứng minh:

a) △ADE ~ △BDC

b) AB.CE + AE.BC = AC.BE.

+ Lời giải

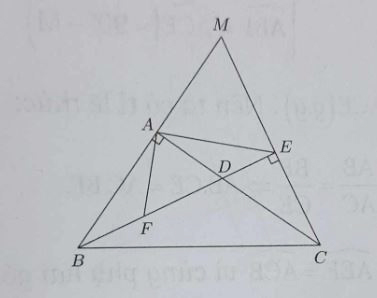
a) Xét △ABD và △ECD có:

• Góc ADB = góc EDC
• Góc BAD = góc CED = 90°

nên △ABD ~ △ECD (g.g). Do đó ta có tỉ lệ thức DA/DB = DE/DC.

Mặt khác △ADE và △BDC có:

• Góc ADE = góc BDC
• DE/DB = DE/DC

Suy ra △ADE ~ △BDC(c.g.c).

b) Gọi M là giao điểm AB và CE.

Xét △MBE và △MCA ta có: Góc M chung và góc MEB = góc MAC (=90°)

Suy ra △MBE ~ △MCA (g.g).

Từ đây, ta có tỉ lệ thức: MB/ME = MC/MA.

Xét △MAE và △MCB có: MC/MA = MB/ME và góc M chung

Suy ra △MAE ~ △MCB (c.g.c).

Do đó góc MEA = góc MBC.

Lấy F ∈ BE sao cho AF⊥AE. Xét △ABF và △ACE có:

Góc BAF = góc CAE (= 90° – góc DAF) và  góc ABF = góc ACE (= 90° – góc M)

Từ đó △ABF ~ △ACE(9.9). Nên ta có tỉ lệ thức:

AC/AB = BF/CE => AB.CE = AC.BF. (1)

Mặt khác, ta có góc AEF = góc ACB vì cùng phụ hai góc bằng nhau.

Xét △AFE và △ABC có góc EAF = góc BAC (= 90°) và góc AEF = góc ACB. Do đó △AFE ~ △ABC(g.g).

Từ đây ta có tỉ lệ thức:

AE/AC = EF/BC => AE.BC AC.EF. (2)

Từ (1), (2) cộng vế với vế ta được:

AB.CE + AE.BC = AC.(BF + EF) = AC.(BF + EF) = AC.BE.

Dạng 7: Sử dụng tam giác đồng dạng để dựng hình

1. Phương pháp giải

• Bước 1. Dựng một tam giác bất kì đồng dạng với tam giác phải dựng.
• Bước 2. Dùng điều kiện về độ dài chưa sử dụng để dựng tiếp.

2. Các ví dụ

Ví dụ 1: Dựng tam giác ABC, biết góc A = 60°, tỉ số AB/AC = 4/5 và đường cao AH = 6cm.

+ Lời giải

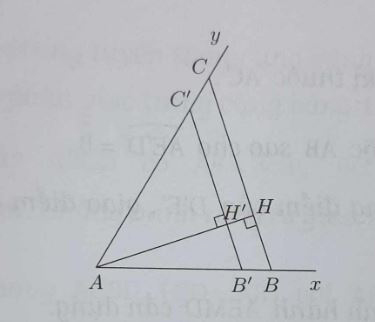
• Bước 1. Dựng △AB’C’ biết góc A = 60° và AB’ = 4, AC’ = 5.

Cách dựng:

Dựng góc xAy = 60°.

Trên tia Ax dựng đoạn AB’ = 4.

Trên tia Ay dựng đoạn AC’ = 5.

• Bước 2. Dựng △ABC ~ △AB’C’ có đường cao AH = 6cm.

Cách dựng:

Dựng đường cao AH’⊥B’C’.

Trên AH’ lấy AH = 6(cm).

Qua H, dựng đường thẳng vuông góc với AH’, cắt Ax và Ay ở B và C.

Ta được tam giác ABC là tam giác cần dựng.

Ví dụ 2: Cho tam giác ABC. Dựng hình bình hành AEMD có D, M, E theo thứ tự thuộc các cạnh AB, BC, CA sao cho các tam giác MDE và ABC đồng dạng.

+ Lời giải

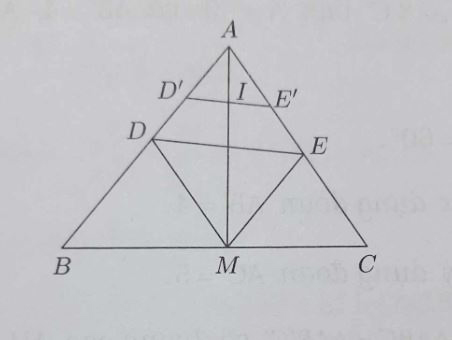
Ta nhận thấy rằng: △MDE = △AED nên cần dựng △AED đồng dạng với △ABC.

Cách dựng:

Dựng E’ bất kì thuộc AC.

Dựng D’ thuộc AB sao cho góc AE’D’ = góc B.

Gọi I là trung điểm của D’E’, giao điểm của AI và BC cho ta điểm M.

Ta được hình bình hành AEMD cần dựng.

Hi vọng bài viết “Bài tập tam giác đồng dạng lớp 8 có đáp án” ở trên sẽ là công cụ đắc lực giúp các em nắm vững một trong những khái niệm cơ bản nhất của hình học: tam giác đồng dạng. 

Để xem thêm lý thuyết và các dạng bài tập về tam giác đồng dạng lớp 8, các em có thể tham khảo thêm cuốn sách Làm chủ kiến thức Toán lớp 8 Phần Hình học.

Link đọc thử sách: https://drive.google.com/file/d/1NhDosmt57ti_t4iZYGXd5evVCVB2bf2M/view

TKbooks tự hảo là nhà xuất bản sách tham khảo lớp 8 hàng đầu tại Việt Nam!

TKbooks.vn