Chưa có sản phẩm trong giỏ hàng.
Mặt nón, mặt trụ và mặt cầu – Lý thuyết, bài tập và cách giải cực chi tiết
Mặt nón, mặt trụ và mặt cầu là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.
Dưới đây là toàn bộ kiến thức về Mặt nón, mặt trụ và mặt cầu. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
I. MẶT NÓN – HÌNH NÓN – KHỐI NÓN
1. Định nghĩa:
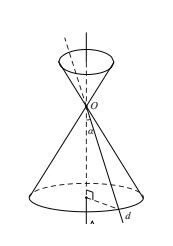
Trong mặt (P) cho hai đường thẳng d và Δ cắt nhau tại điểm O và tạo thành góc α (với 0° < α< 90°).
Khi quay mặt phẳng (P) xung quanh Δ thì đường thẳng d sinh ra một mặt tròn xoay gọi là
mặt nón tròn xoay đỉnh O . Gọi tắt là mặt nón.
+ Δ gọi là trục của mặt nón.
+ d gọi là đường sinh của mặt nón.
+ O gọi là đỉnh của mặt nón.
+ Nếu gọi α là góc giữa d và Δ thì 2α gọi là góc ở đỉnh của mặt nón.
2. Hình nón tròn xoay
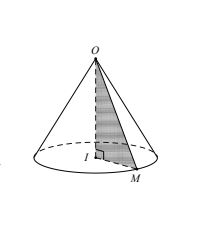
Cho ΔIOM vuông tại I . Khi quay tam giác đó xung quanh cạnh OI thì đường gấp khúc IOM tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.
Trong đó:
+ Hình tròn tâm I sinh bởi các điểm thuộc cạnh IM khi IM quanh OI được gọi là mặt đáy của nón.
+ Điểm O được gọi là đỉnh của hình nón.
+ Độ dài OM được gọi đường sinh của hình nón.
+ Phần mặt tròn xoay sinh bởi các điểm trên cạnh OM khi quay quanh OI được gọi là mặt xung quanh của hình nón.
3. Khối nón tròn xoay
Phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình đó được gọi là khối nón tròn xoay hay còn gọi tắt là khối nón.
Trong đó:
+ Điểm thuộc khối nón nhưng không thuộc hình nón gọi là điểm trong của khối nón.
+ Ta gọi đỉnh, mặt đáy, đường sinh của hình nón theo thứ tự là đỉnh, mặt đáy, đường sinh của khối nón tương ứng.
4. Diện tích hình nón và thể tích khối nón
a. Định nghĩa:
+ Diện tích xung quanh của hình nón là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.
+ Thể tích của khối nón: là giới hạn của thể tích của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.
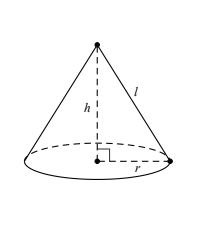
b. Công thức:
Gọi r là bán kính đường tròn đáy; l là độ dài đường sinh; h là đường cao; h là diện tích đáy của hình nón.
- Diện tích xung quanh:
| Sxq = π.r.l |
- Diện tích toàn phần:
| Stp = Sxq + Sđáy = π.r.(r + l) |
- Thể tích khối nón:
| Vnón = 1/3.B.h = 1/3.π.r2.h |

5. Hình nón cụt
a. Định nghĩa:
Hình nón cụt là phần nón giới hạn bởi mặt đáy và một thiết diện song song với đáy.
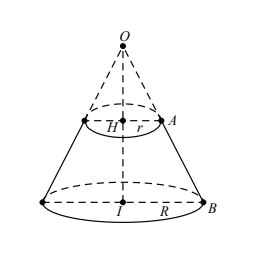
b. Công thức:
- Diện tích xung quanh:
| Sxq = π.l.(R + r) |
- Diện tích toàn phần
| Stp = л.(r² + R² ) + π.l.(R + r) |
- Thể tích khối nón cụt:
| Vnón cụt = 1/3.π.h.(R² + r² + Rr) |
II. MẶT TRỤ – HÌNH TRỤ – KHỐI TRỤ
1. Mặt trụ tròn xoay
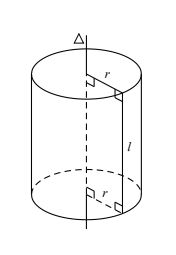
Trong mặt phẳng (P) cho hai đường thẳng Δ và 1 song song với nhau, cách nhau một khoảng bằng r.
Khi quay (P) xung quanh Δ thì 1 sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay.
+ Δ gọi là trục;
+ l gọi là đường sinh;
+ r là bán kính của mặt trụ đó.
2. Hình trụ tròn xoay
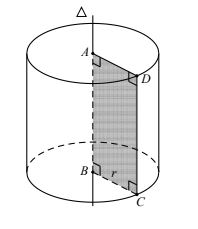
Xét hình chữ nhật ABCD. Khi quay hình đó xung quanh đường thẳng chứa một cạnh, chẳng hạn AB, thì đường gấp khúc ADCB tạo thành một hình được gọi là hình trụ tròn xoay.
+ Hai đáy là hai hình tròn: Tâm A bán kính r = AD và tâm B bán kính r = BC.
+ Đường sinh: đoạn CD.
+ Mặt xung quanh: là mặt do đoạn CD tạo thành khi quay, nếu cắt theo một đường sinh và trải ra ta mặt xung quanh là một hình chữ nhật.
+ Chiều cao: h = AB = CD.
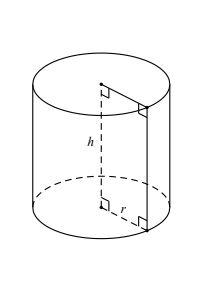
3. Khối trụ tròn xoay
Phần không gian được giới hạn bởi một hình trụ kể cả hình trụ đó được gọi là khối trụ tròn xoay.
4. Diện tích hình trụ và thể tích khối trụ
Diện tích hình trụ và thể tích khối trụ được cho bởi các công thức sau:
Diện tích xung quanh:
| Sxq = 2л.r.h |
Diện tích toàn phần:
| Stp = 2.л.r.(h + r) |
Thể tích khối trụ:
| Vtrụ = π.r².h |

III. MẶT CẦU – HÌNH CẦU – KHỐI CẦU
1. Các định nghĩa
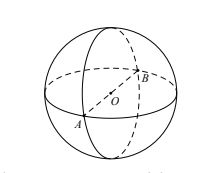
Tập hợp các điểm trong không gian cách điểm cố định O một khoảng R không đổi gọi là mặt cầu tâm O bán kính R.
Ki hiệu: S(O; R).
Tập hợp các điểm M trong không gian sao cho OM < R gọi là khối cầu tâm O, bán kính R.
S(O; R) = {M | OM = R}
Nếu A, B thuộc (S) và AB đi qua O thì AB gọi là đường kính của mặt cầu (S).
2. Vị trí tương đối giữa mặt cầu và mặt phẳng
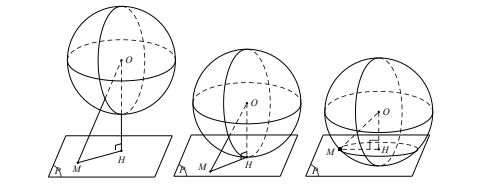
Cho mặt cầu S(O;R) và mặt phẳng (P), gọi d là khoảng cách từ O đến mặt phẳng (P) và H là hình chiếu vuông góc của O lên (P).
Khi đó:
- Nếu d > R thì (P) không cắt mặt cầu (S) .
- Nếu d = R thì (P) tiếp xúc với mặt cầu (S) tại H . Ta nói (P) là tiếp diện của mặt cầu (S), còn H gọi là tiếp điểm của (P) và (S).
- Nếu d < R thì (P) cắt (S) theo giao tuyến là một đường tròn (P) có tâm H và bán kính r = √ (R2 – d2)
Chú ý: Khi d = R thì (P) đi qua tâm O của mặt cầu (S) lúc đó ta gọi (P) là mặt phẳng kính và giao tuyến là đường tròn lớn của mặt cầu.
Mặt cầu đi qua mọi đỉnh của hình đa diện (H) gọi là mặt cầu ngoại tiếp hình đa diện (H) và hình đa diện (H) được gọi là nội tiếp mặt cầu.
Mặt cầu tiếp xúc với tất cả các mặt của hình đa diện (H) gọi là mặt cầu nội tiếp hình đa diện (H ) và hình đa diện (H) được gọi là ngoại tiếp mặt cầu.
3. Vị trí tương đối giữa mặt cầu và đường thẳng
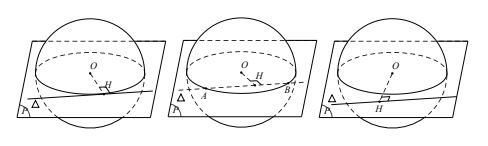
Cho mặt cầu S(O;R) và đường thẳng Δ, gọi H là hình chiếu vuông góc của O lên Δ và d = OH.
Khi đó:
- Nếu d < R thì Δ cắt mặt cầu (S) tại hai điểm phân biệt.
- Nếu d = R thì Δ tiếp xúc với mặt cầu (S) tại một điểm, lúc đó Δ gọi là tiếp tuyến của mặt cầu và H gọi là tiếp điểm của mặt cầu.
- Nếu d > R thì Δ không cắt mặt cầu.
Chú ý:
Qua một điểm 4 nằm trên mặt cầu S(O;R) có vô số tiếp tuyến với mặt cầu. Tất cả các tiếp tuyến này đều vuông góc với bán kính OA và nằm trong mặt phẳng tiếp xúc với mặt cầu tại A.
Định lí: Qua một điểm A nằm ngoài mặt cầu S(O; R) có vô số tiếp tuyến với mặt cầu. Các tiếp tuyến này tạo thành một mặt nón đỉnh A.
- Khi đó, độ dài đường sinh của hình nón là:
| l = √(OA²- R²) |
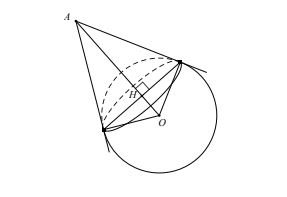
- Đường cao của hình nón là:
| h = AH = OA² – R²)/OA |
4. Diện tích và thể tích của khối cầu và chỏm cầu
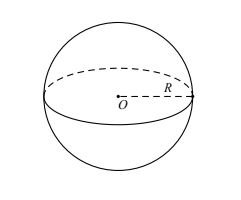
- Diện tích mặt cầu:
| Scầu = 4.π.R2 |
- Thể tích khối cầu:
| Vcầu = 4/3. π.R3 |
- Diện tích chỏm cầu:
| Schỏm cầu = π.(r2 + h2) |
- Thể tích chỏm cầu:
| Vchỏm cầu = [(π.h)/6].(h2 + 3r2) |
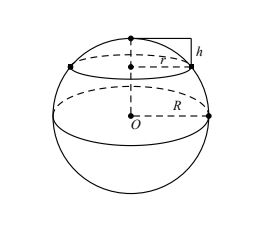
5. Mặt cầu ngoại tiếp khối đa diện
a. Các khái niệm cơ bản
Trục của đa giác đáy: là đường thăng đi qua tâm đường tròn ngoại tiếp của đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy. Bất kì một điểm nào nằm trên trục của đa giác thì cách đều các đỉnh của đa giác đó.
Đường trung trực của đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó. Bất kì một điểm nào nằm trên đường trung trực thì cách đều hai đầu mút của đoạn thẳng.
Mặt trung trực của đoạn thẳng là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó. Bất kì một điểm nào nằm trên mặt trung trực thì cách đều hai đầu mút của đoạn thẳng.
b. Tâm và bán kính mặt cầu ngoaị tiếp hình chóp
Tâm mặt cầu ngoại tiếp hình chóp: là điểm cách đều các đỉnh của hình chóp. Hay nói cách khác, nó chính là giao điểm I của trục đường tròn ngoaị tiếp mặt phẳng đáy và mặt phẳng trung trực của một cạnh bên hình chóp.
Bán kính là khoảng cách từ I đến các định của hình chóp.
c. Cách xác định tâm và bán kính mặt cầu của một số hình đa diện cơ bản
Hình hộp chữ nhật, hình lập phương:
- Tâm: là trung điểm I của AC’.
- Bán kính: R = AC’/2
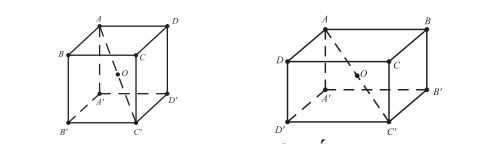
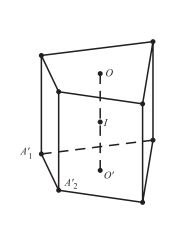
Hình lăng trụ đứng có đáy nội tiếp đường tròn:
Xét lăng trụ đứng A1A2,…An.A1‘A2‘,…An‘, trong đó có 2 đáy A1A2,…An và A1‘A2‘,…An‘ nội tiếp đường tròn (O) và (O’).
- Tâm: là trung điểm I của OO’.
- Bán kính: R = SC/2 = IA = IB = IC
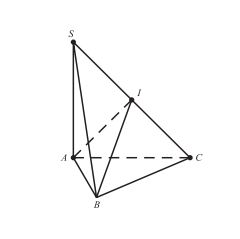
Hình chóp S.ABC có góc SAC = góc SBC = góc SCD = 90°
- Tâm: trung điểm I của SC
- Bán kính: R = SC/2 = IA = IB = IC = ID
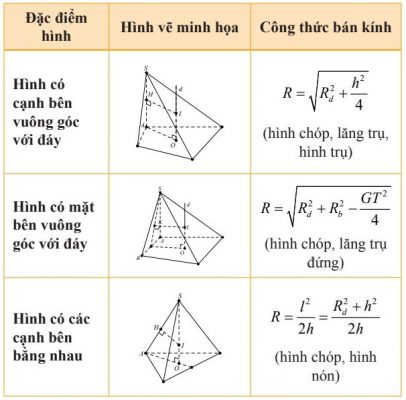
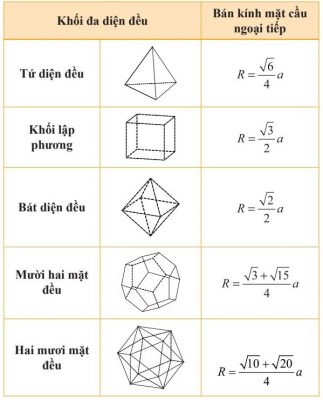
Một số hình khác
Gọi:
+ R: bán kính mặt cầu ngoại tiếp các hình khối cần tính.
+ Rd: bán kính đường tròn ngoại tiếp đáy.
+ Rb: bán kính đường tròn ngoại tiếp mặt bên.
+ l: độ dài cạnh bên.
+ h: độ dài chiều cao.
+ GT: độ dài đoạn giao tuyến của mặt bên với đáy.
IV. Bài tập
Dưới đây là một số dạng toán cơ bản về Mặt nón, mặt trụ và mặt cầu để các em luyện tập:

Các dạng toán khác về Thể tích khối đa diện được ghi chú và diễn giải rất đầy đủ trong cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.

