Tích phân là gì và ứng dụng của tích phân trong tính diện tích và thể tích của vật thể

Tích phân và ứng dụng của tích phân là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.

Dưới đây là toàn bộ kiến thức về Tích phân và ứng dụng của tích phân. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!

I. TÍCH PHÂN LÀ GÌ

1. Khái niệm

Cho hàm số f(x) liên tục trên K và a,b ∈ K.

Hàm số F(x) gọi là nguyên hàm của f(x) trên K thì F(b) – F(a) được gọi là tích phân của f(x) từ a đến b và có ký hiệu:

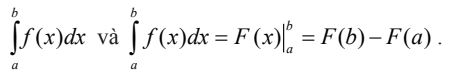
Đối với biến số lấy tích phân, ta có thể chọn bất kỳ một chữ cái khác nhau thay cho x, nghĩa là:

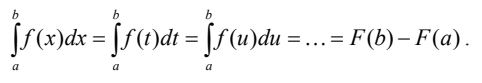
Ý nghĩa hình học:

Nếu hàm số y = f(x) liên tục và không âm trên đoạn [a;b] thì diện tích S của hình thang cong giới hạn bởi đồ thị của y = f(x), trục Ox và hai đường thẳng x = a, x = b là:

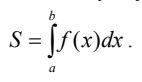
2. Tính chất của tích phân

II. PHƯƠNG PHÁP TÍNH TÍCH PHÂN

1. Phương pháp đổi biến số

Định lí:

Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử hàm số x = Φ(t) có đạo làm liên tục trên đoạn [α; β] sao cho Φ(α) = a; Φ(β) = b và a ≤ Φ(t) ≤ b với mọi t ∈[α; β].

Khi đó:

 

2. Phương pháp tính tích phân từng phần

Định lí:

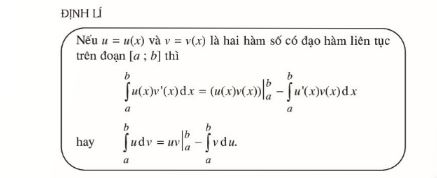
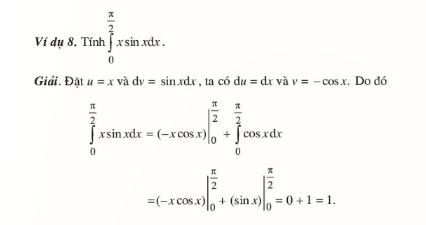
III. ỨNG DỤNG TÍCH PHÂN ĐỂ TÍNH DIỆN TÍCH, THỂ TÍCH CÁC LOẠI HÌNH ĐẶC BIỆT

1. Tính diện tích hình phẳng

Định lí 1:

Cho hàm số y = f(x), y = g(x) liên tục trên [a;b].

• Dạng 1: Diện tích hình phẳng giới hạn bởi các đường

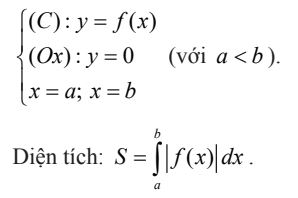
• Dạng 2: Diện tích hình phẳng giới hạn bởi các đường

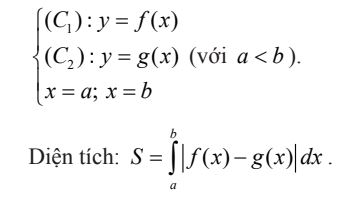
• Dạng 3: Diện tích hình phẳng giới hạn bởi các đường

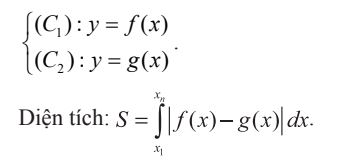
Trong đó: x₁, x_n tương ứng là nghiệm nhỏ nhất, lớn nhất của phương trình: f(x) = g(x).

• Dạng 4: Diện tích hình phẳng giới hạn bởi các đường

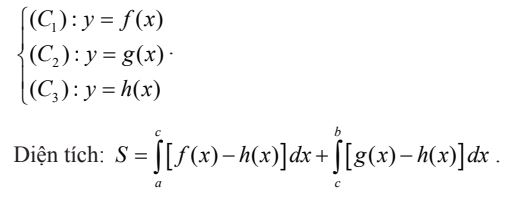
Chú ý:

Để phá bỏ dấu giá trị tuyệt đối ta thường làm như sau:

Giải phương trình: f(x) = g(x) tìm nghiệm x₁, x_2, …, x_n ∈ (a;b) và x₁ < x_2, …, < x_n.

Tính:

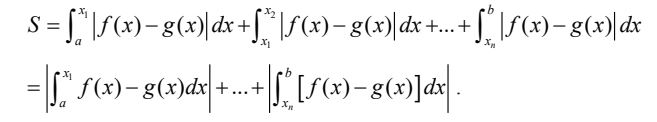
Ngoài cách trên, ta có thể dựa vào đồ thị để bỏ dấu giá trị tuyệt đối.

2. Tính thể tích khối tròn xoay

a. Tính thể tích của vật thể

Định lí 2:

Cắt một vật thể C bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x = a, x = b (a < b). Một mặt phẳng bất kì vuông góc với Ox tại điểm x ( a < x < b) cắt C theo một thiết diện có diện tích S(x).

Giả sử S(x) là hàm liên tục trên [a;b].

Khi đó thể tích của vật thể C giới hạn bởi hai mặt phẳng (P) và (Q) được tính theo công thức:

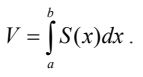
2. Tính thể tích vật tròn xoay

• Dạng 1: Thể tích hình phẳng giới hạn bởi các đường

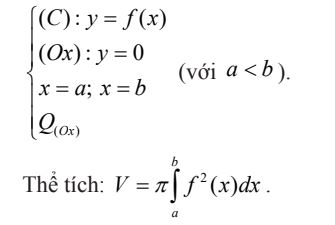
• Dạng 2: Thể tích hình phẳng giới hạn bởi các đường

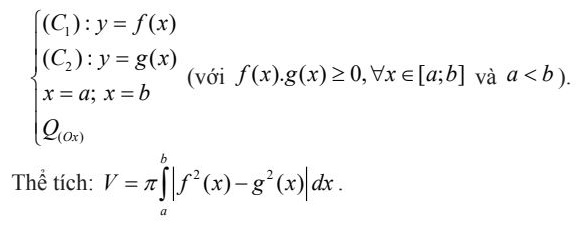
• Dạng 3: Thể tích hình phẳng giới hạn bởi các đường

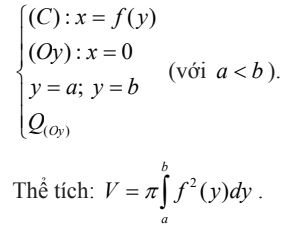
Chú ý: Trong trường hợp ta không tìm được x theo y thì ta có thể giải bài toán theo cách sau:

Chứng minh hàm số y = f(x) liên tục và đơn điệu trên [c;d] với  c= min{g(a),g(b)}, d = max{g(a),g(b)}.

Khi đó phương trình y = f(x) có duy nhất nghiệm x = g(y).

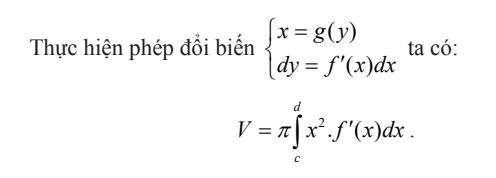
IV. CÁC LỚP TÍCH PHÂN ĐẶC BIỆT

• Dạng 1: Hàm số dưới dấu tích phân là hàm chẵn, lẻ

Bài toán 1: Nếu f(x) là hàm chẵn và liên tục trên đoạn |-a;a] thì:

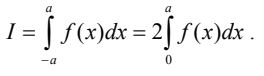
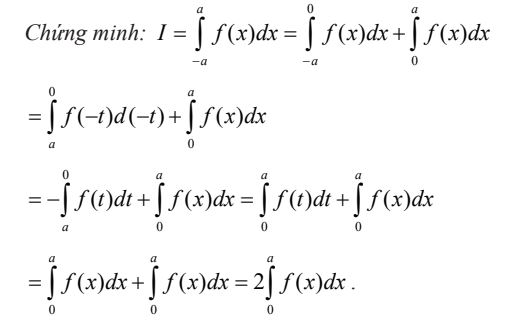
V. LỊCH SỬ CỦA TÍCH PHÂN

Phép tính tích phân đã được các nhà bác học sử dụng từ trước thế kỉ XVIII. Đến kỉ XIX, Cô-si (Cauchy, 1789 – 1857) và Ri-man (Riemann, 1826 – 1866) mới dựng được một lí thuyết chính xác về tích phân. Lí thuyết này về sau được Lơ-be-gơ (Lebesgue, 1875 – 1941) và Đăng gioa (Denjoy, 1884 – 1974) hoàn thiện.

Để định nghĩa tích phân, các nhà toán học ở thế kỉ XVII và XVIII không dùng khái niệm giới hạn. Thay vào đó, họ nói “tổng của một số vô cùng lớn những hạng vô cùng nhỏ”. Chẳng hạn, diện tích của hình thang cong là tổng của một số vô cùng lớn những diện tích của những hình chữ nhật vô cùng nhỏ.

Dựa trên cơ sở này. Kê-ple (Kepler, 1571 – 1630) đã tính một cách chính xác nhiều diện tích và thể tích. Các nghiên cứu này được Ca-va-li-ơ-ri (Cavalierie,1598 – 1647) tiếp tục phát triển.

Dưới dạng trừu tượng, tích phân đã được Lai-bơ-nit định nghĩa và đưa vào kí hiệu J. gọi “tích phân” do Bec-nu-li (Jacob Bernoulli, 1654 – 1705), học trò của Lai-bơ-nit đề xuất.

Như vậy, tích phân đã xuất hiện độc lập với đạo hàm và nguyên hàm. Do đó, thiết lập liên hệ giữa tích phân và nguyên hàm là một phát minh vĩ đại của Niu-tơn và Lai-bơ-nit.

Khái niệm hiện đại về tích phân, xem như giới hạn của các tổng tích phân, là của Cô-si và Ri-man.

VI. BÀI TẬP

Dưới đây là một số dạng toán cơ bản về Tích phân để các em luyện tập:

 

Các dạng toán khác về Tích phân và ứng dụng của tích phân được ghi chú và diễn giải rất đầy đủ trong cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!

Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.

Tkbooks.vn