Đạo hàm lớp 11 – Đạo hàm là gì và ứng dụng của đạo hàm

Đạo hàm lớp 11 là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 15% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.

Dưới đây là toàn bộ kiến thức về đạo hàm lớp 11, bao gồm đạo hàm là gì, ý nghĩa và ứng dụng của đạo hàm. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!

I. ĐẠO HÀM LÀ GÌ VÀ ỨNG DỤNG CỦA ĐẠO HÀM

1. Đạo hàm là gì?

Ví dụ mở đầu:

Quãng đường rơi tự do của một vật được biểu diễn bởi công thức s(t) = 4,9t²  với t là thời gian tính băng giây và s tính bằng mét.

Vận tốc trung bình của chuyển động này trên khoảng thời gian [5; t]| hoặc [t; 5] được tính bằng công thức:

[s(t) – s(5)]/(t – 5)

a) Hoàn thiện bảng sau về vận tốc trung bình trong những khoảng thời gian khác nhau. Nếu nhận xét về [s(t) – s(5)]/(t – 5) khi t càng gần 5.

Khoảng thời gian	[5; 6]	[5; 5,1]	[5; 5,05]	[5; 5,01]	[5; 5,001]	[4,999; 5]	[4,99; 5]
[s(t) – s(5)]/(t – 5)	53,9	?	?	?	?	?	?

Mở rộng tình huống trong hoạt động trên, giả sử s(t) là toạ độ tại thời điểm t của một chất điểm chuyển động thẳng trên trục s’Os (Hình 2).

Khi đó, giới hạn

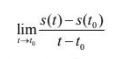
được gọi là vận tốc tức thời của chuyển động tại thời điểm t₀, kí hiểu v(t₀). Giới hạn này cũng được gọi là đạo hàm của hàm số s(t) theo thời gian t tại thời điểm t₀, kí hiệu s(t₀).

Vậy:

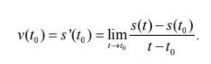
Tổng quát, ta có định nghĩa đạo hàm của hàm số bất kỳ như sau:

2. Đạo hàm tại một điểm

a. Định nghĩa đạo hàm tại một điểm

Cho hàm số y = f (x) xác định trên khoảng (a;b) và x₀ ∈ (a;b)

Nếu tồn tại giới hạn (hữu hạn)

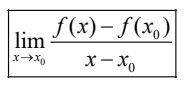
thì giới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại x₀ và kí hiệu là f'(x₀) (hoặc y'(x₀) ), tức là:

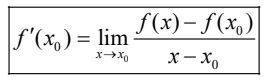
Chú ý:

Đại lượng Δx = x − x₀ gọi là số gia của đối số x tại x₀.

Đại lượng Δy = f(x) – f(x₀) = f (x₀ + Δx) − f(x₀) được gọi là số gia tương ứng của hàm số. Như vậy:

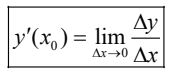
b. Cách tính đạo hàm bằng định nghĩa

• Bước 1: Giả sử Δx là số gia của đối số x tại x₀, tính

Δy = f (x₀ + Δx) − f(x₀).

• Bước 2: Lập tỉ số Δy/Δx

Chú ý: Trong định nghĩa và quy tắc trên đây, thay x₀ bởi x ta sẽ có định nghĩa và quy tắc tính đạo hàm của hàm số y = f(x) tại điểm x ∈ (a;b).

• Bước 3: Tìm:

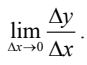
c. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số

Định lí 1

Nếu hàm số y = f (x) có đạo hàm tại x₀ thì nó liên tục tại x₀.

+ Chú ý:

Nếu y = f(x) gián đoạn tại x₀ thì nó không có đạo hàm tại x₀

Nếu y= f(x) liên tục tại x₀ thì có thể không có đạo hàm tại x₀.

Chẳng hạn: Xét hàm f (x) = |x| liên tục tại x = 0 nhưng không liên tục tại điểm đó.

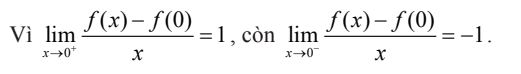
d. Ý nghĩa hình học của đạo hàm

Định lí 2

Đạo hàm của hàm số y = f(x) tại điểm x₀ là hệ số góc của tiếp tuyến M₀T của đồ thị hàm số tại điểm M₀(x₀; f(x₀)).

Định lí 3

Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M₀(x₀; f(x₀)) là:

y = f'(x₀)(x – x₀) + y₀ trong đó y₀ = f(x₀).

e. Ý nghĩa vật lý của đạo hàm

Vận tốc tức thời: v₀(t) = s'(t₀)

Cường độ tức thời: I(t₀) = Q'(t₀)

3. Đạo hàm trên một khoảng

Định nghĩa

Hàm số y = f(x) được gọi là có đạo hàm trên khoảng (a;b) nếu nó có đạo hàm tại mọi điểm x trên khoảng đó.

Khi đó, ta gọi hàm số f’ : (a;b)→ R

x |→ f'(x)

là đạo hàm của hàm số y= f(x) trên khoảng (a;b), kí hiệu là y’ hay f'(x).

4. Ứng dụng của đạo hàm

a. Số e

Một người gửi tiết kiệm khoan tiền A triệu đồng (gọi là vốn) với lãi suất n/năm theo thể thức lãi kép (tiền lãi sau mỗi kì hạn được cộng gộp vào vốn). Tính tổng số tiền vốn và lãi sau một năm của người gửi nếu kì hạn là:

1. a) một năm
2. b) một tháng.

Lưu ý. Nếu một năm được chia thành n kì hạn (n∈N) thì lãi suất mỗi ki hạn là r/n.

Xét tình huống gửi tiết kiệm ở trên. Kí hiệu T là tổng số tiền vốn và lãi của người gửi sau một năm. Tùy theo kì hạn, ta có những công thức tính T khác nhau.

• Nếu kì hạn là 1 năm thì T = A.(1 + r)
• Nếu kì hạn là 6 tháng thì T = A.(1 + r/2)²
• Nếu kì hạn là 3 tháng thì T = A.(1 + r/4)⁴
• Nếu kì hạn là 1 tháng thì T = A.(1 + r/12)¹²
• Nếu kì hạn là 1 ngày thì T = A.(1 + r/365)³⁶⁵ luôn coi một năm có 365 ngày).

Tổng quát, nếu một năm được chia thành n kì hạn thì:

T = A.(1 + r/n)ⁿ = A.(1 + 1/m)^m (với m = n/r, r > 0)

Khi kì hạn càng ngắn thì n càng lớn, do đó m càng lớn. Người ta chứng minh được rằng có giới hạn hữu hạn:

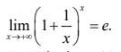
Hơn nữa, người ta còn biết rằng e là số vô tỉ và e = 2,718281828… (số thập phân vô hạn không tuần hoàn)

Từ kết quả trên suy ra, khi kì hạn trở nên rất ngắn (m dần đến +∞) thì .(1 + 1/m)^m dần đến e, và do đó T = A.(1 + 1/m)^m dần đến A.e^r

Số e xuất hiện trong nhiều bài toán ở những lĩnh vực khác nhau như Toán học, Vật lí, Sinh học, Kinh tế, …. cũng chính là ứng dụng của đạo hàm.

b. Ứng dụng của đạo hàm trong tính lãi kép

Công thức T= A.e^rt được dùng để tính tổng số tiền vốn và lãi mà người gửi nhận được sau thời gian T kể từ thời điểm người đó gửi tiết kiệm A đồng theo thể thức “lãi kép liên tục” với lãi suất r/năm. Trong đó A và T tính theo đồng, t tính theo năm và t có thể nhận giá trị thực bất kì. Sử dụng máy tính cầm tay, tính giá trị của T (làm tròn đến hàng đơn vị) khi A = 2.000.000, r = 0,05 và:

1. a) t = ¼;
2. b) t = 1/365.

Giải:

a) T = 2000000.e0.05.1/4 = 2000000.e0.0125 ≈ 2025157 (đồng).

b) T = 2000 000.e0.05.1/365 = 2000274 (đồng).

5. Bài tập về đạo hàm

Dưới đây là một số dạng toán cơ bản về Đạo hàm để các em luyện tập:

Các dạng toán khác về Đạo hàm được ghi chú và diễn giải rất đầy đủ trong cuốn  cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!

Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.

Tkbooks.vn