Chưa có sản phẩm trong giỏ hàng.
Dãy số, cấp số cộng, cấp số nhân – Lý thuyết, bài tập và cách giải cực chi tiết
Dãy số, cấp số cộng và cấp số nhân là kiến thức rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì thế các em cần nắm chắc phần này để đạt được điểm số tối ưu.
Dưới đây là toàn bộ kiến thức về dãy số, cấp số cộng và cấp số nhân. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
I. PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
Để chứng minh những mệnh đề liên quan đến số tự nhiên n∈N* là đúng với mọi n mà không thể thử trực tiếp thì có thể làm như sau:
- B1: Kiểm tra rằng mệnh đề đúng với n =1.
- B2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k > 1 (gọi là giả thiết quy nạp), chứng minh rằng nó cũng đúng với n = k + 1.
Đó là phương pháp quy nạp toán học, hay còn gọi tắt là phương pháp quy nạp.
Chú ý: Nếu phải chứng minh mệnh đề là đúng với mọi số tự nhiên n > p (với p là một số tự nhiên) thì:
- B1: Ta phải kiểm tra mệnh đề đúng với n = p;
- B2: Giả thiết mệnh đề đúng với số tự nhiên bất kì n = k > p và phải chứng minh rằng nó cũng đúng với n = k + 1.
Phép thử với một số hữu hạn số tự nhiên, tuy không phải là chứng minh, nhưng cho phép ta dự đoán được kết quả. Kết quả này chỉ là giả thiết, và để chứng minh ta có thể dùng phương pháp quy nạp toán học.
II. DÃY SỐ
1. Định nghĩa dãy số
Mỗi hàm số u xác định trên tập các số nguyên dương N* được gọi là một dãy số vô hạn (gọi tắt là dãy số).
Kí hiệu:
| u: N* →R n |→ u(n). |
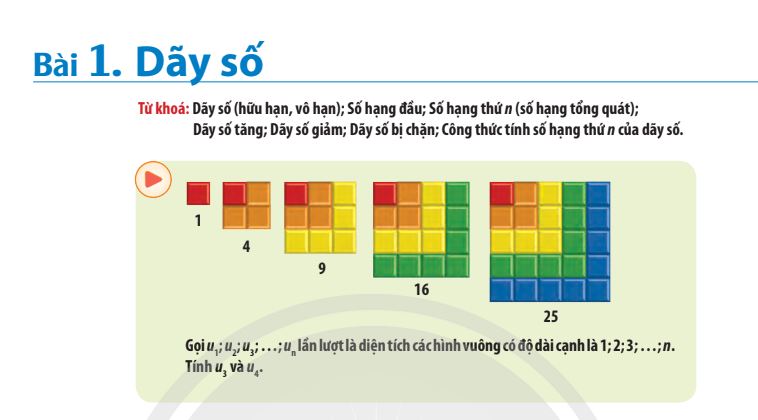
Người ta thường viết dãy số dưới dạng khai triển u1, u2, u3, …, un, …,
trong đó u, = u(n) hoặc viết tắt là (u,) và gọi u, là số hạng đầu, un là số hạng thứ n và là số hạng tổng quát của dãy số.

2. Định nghĩa dãy số hữu hạn
Mỗi hàm số u xác định trên tập M ={1,2,3,…,m} với m∈N* được gọi là một dãy số hữu hạn.
Dạng khai triển của nó là u1, u2, u3, …, un, trong đó u1 là số hạng đầu, un là số hạng cuối.

3. Cách cho một dãy số
a) Dãy số cho bằng công thức của số hạng tổng quát
Khi đó u, = f(n) với f là một hàm số xác định trên N*. Đây là cách khá thông dụng (giống như hàm số) và nếu biết giá trị của n (hay cũng chính là số thứ tự của số hạng) thì ta có thể tính ngay được u, .
b) Dãy số cho bằng phương pháp mô tả
Người ta cho một mệnh để mô tả cách xác định các số hạng liên tiếp của dãy số. Tuy nhiên, không thể tìm ngay được u, với n tùy ý.
c) Dãy số cho bằng công thức truy hồi (hay quy nạp)
+ Cho số hạng thứ nhất u, (hoặc vài số hạng đầu).
+ Với n ≥ 2, cho một công thức tính u, nếu biết vài số hạng đứng ngay trước nó). Các công thức có thể là:
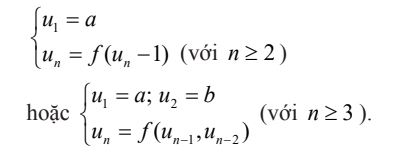
4. Dãy số tăng, dãy số giảm và dãy số bị chặn
a) Dãy số tăng, dãy số giảm
Định nghĩa 1
Dãy số (u,) được gọi là dãy số tăng nếu un+1 > un với mọi n∈N*.
Dãy số (u,) được gọi là dãy số giảm nếu un+1 < un với mọi n∈N*.

Phương pháp khảo sát tính đơn điệu:
+ Phương pháp 1: Xét hiệu H = un+1 – un
- Nếu H > 0 với mọi n∈N* thì dãy số tăng.
- Nếu H < 0 với mọi n∈N* thì dãy số giảm.
+ Phương pháp 2: Nếu un > 0 với mọi n∈N* thì lập tỉ số un+1/un:
- Nếu un+1/un > 1 với mọi n∈N* thì dãy số tăng.
- Nếu un+1/un < 1 với mọi n∈N* thì dãy số giảm.
Chú ý: Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn, dãy số (un) với un = (−3)n tức là dãy –3, 9, -27, 81,… không tăng cũng không giảm.
b) Dãy số bị chặn
Định nghĩa 2:
Dãy số (un) được gọi là bị chặn trên nếu tồn tại một số M sao cho:
| un ≤ M, ∀n ∈ N* |
Dãy số (un) được gọi là bị chặn dưới nếu tồn tại một số n sao cho:
| un ≥ m, ∀n ∈ N* |
Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho:
| m ≤ un ≤ M, ∀n ∈ N* |
Chú ý: Các dấu “=” không nhất thiết phải xảy ra.
III. CẤP SỐ CỘNG
1. Định nghĩa
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đối d.
Số d được gọi là công sai của cấp số cộng.
Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi:
| Un+1 = Un + d (với n∈N*). |
Đặc biệt khi d =0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau).

2. Số hạng tổng quát
Định lí 1
Nếu cấp số cộng (un) có số hạng đầu u, và công sai d thì số hạng tổng quát un được xác định bởi công thức:
| un = u1 + (n-1)d (với n > 2). |
3. Tính chất các số hạng của cấp số cộng
Định lí 2
Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình cộng của hai số hạng đứng kề với nó, nghĩa là:
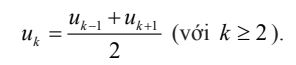

4. Tổng n số hạng đầu của một cấp số cộng
Định lí 3
Cho cấp số cộng (un) . Đặt Sn = u1 + u2 + u3 + … + un. Khi đó:

IV. CẤP SỐ NHÂN
1. Định nghĩa
Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
Nếu (un) là cấp số nhân với công bội q ta có công thức truy hồi:
| Un+1 = un.q (với n∈N*). |
Đặc biệt:
Khi q = 0, cấp số nhân có dạng u, 0, 0, …, 0, …
Khi q =1, cấp số nhân có dạng u1, u1, u1, …, u1,…
Khi u1 = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, …, 0, …

2. Số hạng tổng quát
Định lí l
Nếu cấp số nhân có số hạng đầu u1 và công bội q thì số hạng tổng quát un được xác định bởi công thức:
| Un = u1.qn-1 (với n ≥ 2). |

3. Tính chất các số hạng của cấp số nhân
Định lí 2
Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là:
| u2k = uk-1.uk+1 (với k > 2). |
4. Tổng n số hạng đầu tiên của một cấp số nhân
Định lí 3
Cho cấp số nhân (un) với công bội q = 1.
Đặt Sn = u1 + u2 + … + un. Khi đó:
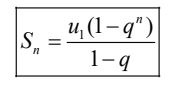
VI. Bài tập luyện tập
Dưới đây là một số dạng toán cơ bản về Dãy số, cấp số cộng và cấp số nhân để các em luyện tập:
1. Bài tập về dãy số

2. Bài tập về cấp số cộng

3. Bài tập về cấp số nhân

Các dạng toán khác về Dãy số, cấp số cộng và cấp số nhân được ghi chú và diễn giải rất đầy đủ trong cuốn cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này về để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.