Chưa có sản phẩm trong giỏ hàng.
Bài tập lũy thừa lớp 6 kèm tổng hợp kiến thức dưới dạng sơ đồ tư duy
Bài viết dưới đây sẽ giới thiệu đến các em bài tập lũy thừa lớp 6 và các công thức lũy thừa lớp 6 dưới dạng sơ đồ tư duy, kèm theo các bài tập thực hành được chia thành các dạng toán với lời giải chi tiết giúp học sinh củng cố kiến thức một cách toàn diện.
Mời các em tham khảo!
>>> Xem thêm: Đề thi khảo sát chất lượng đầu năm lớp 6 môn Toán, Ngữ Văn, Tiếng Anh kèm đáp án
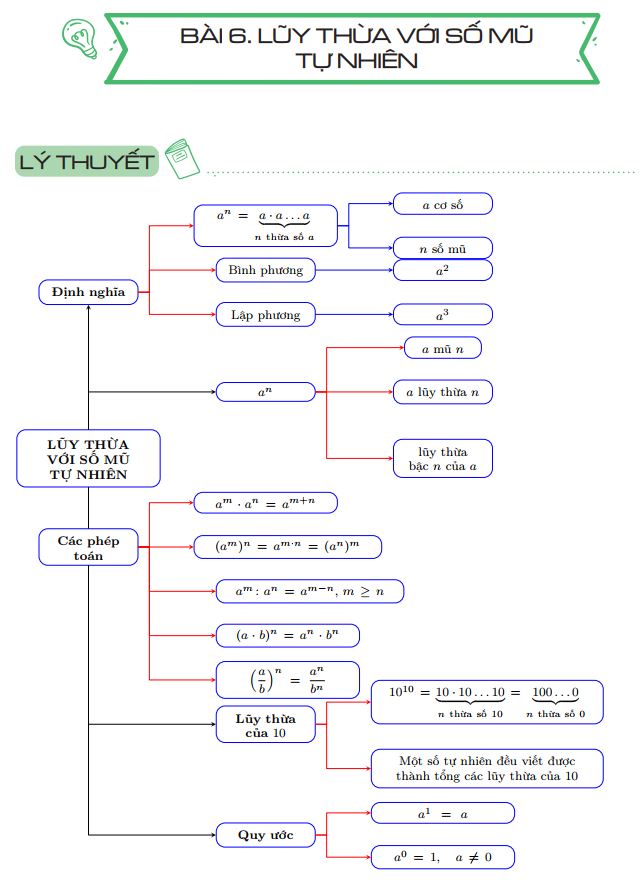
I. Các công thức lũy thừa lớp 6
1. Lũy thừa với số mũ tự nhiên
an = a × a × … × a (n thừa số a, với n là số tự nhiên).
Ví dụ: 23 = 2 x 2 x 2 = 8.
2. Nhân hai lũy thừa cùng cơ số
am x an = am + n.
Ví dụ: 23 x 24 = 23 + 4 = 27.
3. Chia hai lũy thừa cùng cơ số
am : an = am – n.
Ví dụ: 25 : 22 = 25 – 2 = 23.
4. Lũy thừa của một lũy thừa
(am)n = am x n.
Ví dụ: (23)2 = 23 x 2 = 26.
5. Lũy thừa của một tích
(a x b)n = an x bn.
Ví dụ: (2 x 3)2 = 22 x 32 = 4 x 9 = 36.
6. Lũy thừa của một thương
(a/b)n = (an/bn) (với b≠0).
Ví dụ: (2/3)2 = (22/32) = 4/9.
7. Lũy thừa với số mũ 0
a0 = 1 (với a≠0).
Ví dụ: 50 = 1.
8. Lũy thừa với số mũ 1
a1 = a.
Ví dụ: 71 = 7.
II. Các dạng toán về lũy thừa lớp 6 kèm lời giải chi tiết
Dạng 1: Dùng lũy thùa để viết gọn các tích nhiều thừa số giống nhau
1. Phương pháp
Biến đổi để xuất hiện các thừa số giống nhau.
Áp dụng quy tắc: a.a.a…a = an (n thừa số).
2. Các ví dụ
Ví dụ 1:
Viết gọn các tích sau bằng cách dùng lũy thừa:
a) 7.7.7.7;
b) 3.5.15.15;
c) 2.2.5.2.5;
d) 1000.10.10;
e) a.a.a.b.b.b.b;
g) x.x.x + y.y.y.
Hướng dẫn giải
a) 7.7.7.7 = 74.
b) 3.5.15.15 = 15.15.15 = 153.
c) 2.2.5.2.5 = 23.52.
d) 1000.10.10 = 10.10.10.10.10 = 105.
e) a.a.a.b.b.b.b = a3.b4.
g) x.x.x + y.y.y = x3 + y3.
Ví dụ 2: Viết các số sau dưới dạng một lũy thừa với cơ số cho trước:
a) 27, cơ số 3;
b) 125, cơ số 5;
c) 256, cơ số 4;
d) 256, cơ số 2.
Hướng dẫn giải
a) 27 = 3.3.3 = 33.
c) 256 = 4.4.4.4 = 44.
b) 125 = 5.5.5 = 53.
d) 256 = 2.2.2.2.2.2.2.2 = 28.
Dạng 2: Nhân, chia hai lũy thừa cùng cơ số
1. Phương pháp
Dùng công thức am.an = am + n ( chú ý giữ nguyên cơ số, cộng các số mũ);
Dùng công thức am : an = am – n ( chú ý giữ nguyên cơ số, trừ các số mũ).
2. Ví dụ
Viết kết quả phép tính sau dưới dạng lũy thừa:
a) 163.24;
b) a4.a.a2;
c) a4 : a (a≠0);
d) 415 : 45;
e) 46 : 46;
g) 98 : 32.
Hướng dẫn giải
a) 163.24 = 163.16 = 163 + 1 = 164.
b) a4.a.a2 = a4 + 1 + 2 = a7
c) a4 : a = a4 -1 = a3.
d) 415 : 45 = 415 – 5 = 410
e) 98 : 32 = 98 : 9 = 98 – 1 = 9
Dạng 3: Viết một số dưới dạng tổng các lũy thừa của 10
1. Phương pháp
Viết abcd thành a.103 + b.102 + c.101 + d.100.
2. Ví dụ
Viết mỗi số sau dưới dạng tổng các lũy thừa của 10:
a) 234;
b) 2056;
c) 2670.
Hướng dẫn giải
a) 234 = 2.102 + 3.101 + 4.100.
b) 2056 = 2.103 + 0.102 + 5.101 + 6.100.
c) 2670 = 2.103 + 6.102 + 7.101 + 0.100.
Dạng 4: Tìm số mũ hoặc cơ số của một lũy thừa
1. Phương pháp
Ta đưa về hai lũy thừa bằng nhau:
- Trường hợp số mũ bằng nhau, chẳng hạn an = bn thì a = b.
- Trường hợp cơ số bằng nhau, chẳng hạn am = an
+ Nếu a ≠ 0, a ≠ 1 thì m = n;
+ Nếu a = 0 thì m, n là số tự nhiên bất kì khác 0;
+ Nếu a = 1 thì m, n là số tự nhiên bất kì.
2. Các ví dụ
Ví dụ 1: Tìm số tự nhiên n, biết:
a) 2n = 8;
b) 7n = 49;
c) 4n = 64;
d) 5n = 625.
Hướng dẫn giải
a) 2n = 8 → 2n = 23 → n = 3.
b) 7n = 49 → 7n = 72 → n = 2.
c) 4n = 64 → 4n = 44 → n = 4.
d) 5n = 625 → 5n = 54 → n = 4.
Ví dụ 2: Tìm số tự nhiên x, sao cho:
a) 2x.4 = 16;
b) 64.4x = 168;
Hướng dẫn giải
a) 2x.4 = 16 → 2x = 16 : 4 → 2x = 4 → 2x = 22 → x = 2.
b) 64.4x = 168 → 43.4x = (42)8 → 43 + x = 416 → 3 + x = 16 → x = 13.
Dạng 5: Bài toán về số chính phương
Ví dụ:
a) Vì sao số chính phương không tận cùng bởi các chữ số 2, 3, 7, 8?
b) Tổng (hiệu) sau có là số chính phương không?
3.5.7.9.11 + 3;
2.3.4.5.6 – 3.
Hướng dẫn giải
a)
| Tận cùng của a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Tận cùng của a2 | 0 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 |
Tận cùng của số chính phương a không thể bằng 2, 3, 7, 8.
b) Trong tích 3.5.7.9.11 có thừa số 5 nên tích có chữ số tận cùng là 5, tổng là số có tận cùng bằng 8.
Tích 2.3.4.5.6 có chữ số tận cùng là 0 (vì 2.5 = 10 ), hiệu là số có tận cùng bằng 7. Vậy chúng không phải là số chính phương.
III. Bài tập lũy thừa với số mũ tự nhiên trong sách giáo khoa Toán lớp 6
1.36. Viết các tích sau dưới dạng một lũy thừa:
a) 9 · 9 · 9 · 9 · 9;
b) 10 · 10 · 10 · 10;
c) 5 · 5 · 5 · 25;
d) a · a · a · a · a.
Giải
a) 9 · 9 · 9 · 9 · 9 = 95
b) 10 · 10 · 10 · 10 = 104
c) 5 · 5 · 5 · 25 = 55
d) a · a · a · a · a = a5
1.37. Hoàn thành bảng sau vào vở:
| Lũy thừa | Cơ số | Số mũ | Giá trị của lũy thừa |
| 4³ | ? | ? | ? |
| ? | 3 | 5 | ? |
| ? | 2 | ? | 128 |
Giải
| Lũy thừa | Cơ số | Số mũ | Giá trị của lũy thừa |
| 4³ | 4 | 3 | 64 |
| 35 | 3 | 5 | 243 |
| 27 | 2 | 7 | 128 |
1.38. Tính:
a) 2⁵;
b) 3³;
c) 5²;
d) 10⁹.
Giải
a) 2⁵ = 32
b) 3³ = 9
c) 5² = 25
d) 10⁹ = 1000000000.
1.39. Viết các số sau thành tổng giá trị các chữ số của nó bằng cách dùng các lũy thừa của 10: 215; 902; 2 020; 883 001.
Giải
215 = 2 x 102 + 1 x 101 + 5 x 100
902 = 9 x 102 + 0 x 101 + 2 x 100
2020 = 2 x 103 + 0 x 102 + 2 x 101 + 0 x 100
883001 = 8 x 105 + 8 x 104 + 3 x 103 + 0 x 102 + 0 x 101 + 1 x 100
1.40. Tính 11², 111². Từ đó hãy dự đoán kết quả của 1 111².
Giải
112 = 121
1112 = 12321
Dự đoán 11112 = 1234321 (theo quy luật tam giác).
1.41. Biết 2¹⁰ = 1 024. Hãy tính 2⁹ và 2¹¹.
Giải
29 = 210/2 = 1024/2 = 512
211 = 210 x 2 = 1024 x 2 = 2048
1.42. Tính:
a) 5⁷ : 5³;
b) 5⁸ : 5⁴.
Giải
a) 5⁷ : 5³ = 57 – 3 = 54 = 625
b) 5⁸ : 5⁴ = 58 – 4 = 54 = 625
1.43. Ta có: 1 + 3 + 5 = 9 = 3².
Viết các tổng sau dưới dạng bình phương của một số tự nhiên:
a) 1 + 3 + 5 + 7;
b) 1 + 3 + 5 + 7 + 9.
Giải
a) 1 + 3 + 5 + 7 = 16 = 42
b) 1 + 3 + 5 + 7 + 9 = 25 = 52
(Quy luật: Tổng n số lẻ đầu tiên = n2).
1.44.
Trái Đất có khối lượng khoảng 6 000 000 000 000 000 000 000 000 tấn. Mỗi giây Mặt Trời tiêu thụ 6 · 10²⁶ tấn khí hydrogen (theo vnexpress.net).
Nếu Mặt Trời cân bao nhiêu giây để tiêu thụ hết lượng khí hydrogen có khối lượng bằng khối lượng Trái Đất?
Giải
Khối lượng Trái Đất: 6 x 1024 tấn
Mỗi giây Mặt Trời tiêu thụ 6 x 1026 tấn
Thời gian = (6 x 1024)/(6 x 1026) = 10-2 = 0,01 giây
=> Chỉ cần 0,01 giây để tiêu thụ hết lượng khí hydrogen có khối lượng bằng khối lượng Trái Đất?
1.45.
Theo các nhà khoa học, mỗi giây cơ thể người trung bình tạo ra khoảng 25 · 10⁶ tế bào hồng cầu (theo www.healthline.com).
Hãy tính xem mỗi giờ, bao nhiêu tế bào hồng cầu được tạo ra?
Giải
Mỗi giây: 25 x 106 = 25000000 tế bào
Mỗi giờ: 25 x 106 x 3600 = 90000000000 tế bào
Vậy mỗi giờ sẽ có 90 tỷ tế bào hồng cầu được tạo ra.
Hy vọng các công thức lũy thừa lớp 6 dưới dạng sơ đồ tư duy kèm bài tập và lời giải chi tiết ở trên sẽ giúp các em học sinh có cái nhìn toàn diện hơn về các dạng toán lũy thừa cũng như có thêm tài liệu tham khảo hữu ích để rèn luyện.
Hãy tiếp tục ôn tập và thực hành nhiều hơn để làm chủ kiến thức và đạt được kết quả tốt trong học tập.
Đừng quên Tkbooks có bộ sách Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 6 cực chất lượng giúp các em củng cố kiến thức cũng như nâng cao điểm số của mình ở trên lớp. Hãy mua sách và luyện tập ngay từ bây giờ để không bỏ lỡ những cơ hội học tập tuyệt vời các em nhé!
Link đọc thử và mua sách với giá cực ưu đãi: https://lamchu.tkbooks.vn/lop6
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 6 hàng đầu tại Việt Nam!


